前言
理解神经网络中的向前传播和向后传播计算对于理解神经网络工作机制是很重要的。吴恩达老师的视频是通过列举具体的公式和数据,还原向前传播和向后传播计算过程,来让我们理解他们的。
总之这个地方对于导数的知识是有要求的,但是由于我们老师已经开始讲数据挖掘预测了,我这博客更新的内容还处于初级阶段,所以导数的内容我不再赘述,需要补数学的同学去哔哩哔哩搜索宋浩老师,看有关导数的几节视频就可以了,其他的像贝叶斯以后会用到,现在看也行,以后看也行。
废话不多说,我们开讲。
向前传播和向后传播
深度学习指的是数以百千层的层数很深的神经网络,每层又有数以百千个神经元。那么深度学习是否也可以使用这种形式的梯度下降来进行调节权重呢?答:很难。为什么?主要原因是太深了。为何“深”用梯度下降解会有问题呢?主要是因为链式法则导致计算损失函数对前面层权重的导数时,损失函数对后面层权重的导数总是被重复计算,反向传播就是将那些计算的值保存减少重复计算。不明白?那这篇文章就看对了。接下来将解释这个重复计算过程。反向传播就是梯度下降中的求导环节,它从后往前计算导数重复利用计算过的导数而已。
可以说,一个神经网络的计算,都是按照前向或反向传播过程组织的。
首先我们计算出一个新的网络的输出(前向过程),紧接着进行一个反向传输操作。
后者我们用来计算出对应的梯度或导数。计算图解释了为什么我们用这种方式组织这些计算过程。在这篇笔记中中,我们将举一个例子说明计算图是什么。让我们举一个比逻辑回归更加简单的,或者说不那么正式的神经网络的例子。

我们尝试计算函数J,J是由三个变量a,b,c组成的函数,这个函数是3(a+bc) 。计算这个函数实际上有三个不同的步骤,首先是计算 b 乘以 c,我们把它储存在变量u中,因此u=bc; 然后计算v=a+u;最后输出J=3v,这就是要计算的函数J。
我们可以把这三步画成如下的计算图,我先在这画三个变量a,b,c,第一步就是计算u=bc,我在这周围放个矩形框,它的输入是b,c,接着第二步v=a+u,最后一步J=3v。
举个例子: a=5,b=3,c=2 ,u=bc就是6,就是5+6=11。J是3倍的 ,因此。即3×(5+3×2)。如果你把它算出来,实际上得到33就是J的值。 当有不同的或者一些特殊的输出变量时,例如本例中的J和逻辑回归中你想优化的代价函数J,因此计算图用来处理这些计算会很方便。从这个小例子中我们可以看出,通过一个从左向右的过程,你可以计算出J的值。为了计算导数,从右到左(红色箭头,和蓝色箭头的过程相反)的过程是用于计算导数最自然的方式。
概括一下:计算图组织计算的形式是用蓝色箭头从左到右的计算,让我们看看如何进行反向红色箭头(也就是从右到左)的导数计算
计算图的导数计算(Derivatives with a Computation Graph)
在上一个视频中,我们看了一个例子使用流程计算图来计算函数J。现在我们清理一下流程图的描述,看看你如何利用它计算出函数J的导数。
下面用到的公式:

这是一个流程图:

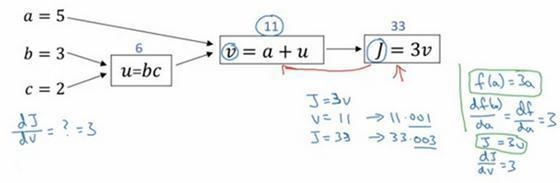
假设你要计算dJ/dv,那要怎么算呢?
好,比如说,我们要把这个v值拿过来,改变一下,那么J的值会怎么变呢?
所以定义上J=3v,现在v=11,所以如果你让v增加一点点,比如到11.001,那么J=3v=33.003,所以我这里v增加了0.001,然后最终结果是J上升到原来的3倍,所以dJ/dv=3,因为对于任何 v 的增量J都会有3倍增量,而且这类似于我们在上一个视频中的例子,我们有f(a)=3a,然后我们推导出(df(a))/da=3,所以这里我们有J=3v,所以dJ/dv=3,这里J扮演了f的角色,在之前的视频里的例子。
在反向传播算法中的术语,我们看到,如果你想计算最后输出变量的导数,使用你最关心的变量对v的导数,那么我们就做完了一步反向传播,在这个流程图中是一个反向步。
我们来看另一个例子,dJ/da是多少呢?换句话说,如果我们提高a的数值,对J的数值有什么影响?
好,我们看看这个例子。变量a=5,我们让它增加到5.001,那么对v的影响就是a+u,之前v=11,现在变成11.001,我们从上面看到现在J就变成33.003了,所以我们看到的是,如果你让a增加0.001,J增加0.003。那么增加a,我是说如果你把这个5换成某个新值,那么a的改变量就会传播到流程图的最右,所以J最后是33.003。所以J的增量是3乘以a的增量,意味着这个导数是3。

要解释这个计算过程,其中一种方式是:如果你改变了a,那么也会改变v,通过改变v,也会改变J,所以J值的净变化量,当你提升这个值(0.001),当你把a值提高一点点,这就是J的变化量(0.003)。

首先a增加了,v也会增加,v增加多少呢?这取决于dv/da,然后v的变化导致J也在增加,所以这在微积分里实际上叫链式法则,如果a影响到v,v影响到J,那么当你让a变大时,J的变化量就是当你改变a时,v的变化量乘以改变v时J的变化量,在微积分里这叫链式法则(其实就是高中学的的复合函数求导)。
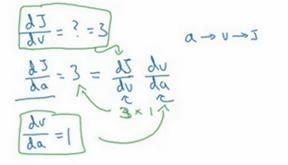
我们从这个计算中看到,如果你让a增加0.001,v也会变化相同的大小,所以dv/da=1。事实上,如果你代入进去,我们之前算过dJ/dv=3,dv/da=1,所以这个乘积3×1,实际上就给出了正确答案,dJ/da=3。
这张小图表示了如何计算,dJ/dv就是J对变量v的导数,它可以帮助你计算dJ/da,所以这是另一步反向传播计算。

现在我想介绍一个新的符号约定,当你编程实现反向传播时,通常会有一个最终输出值是你要关心的,最终的输出变量,你真正想要关心或者说优化的。在这种情况下最终的输出变量是J,就是流程图里最后一个符号,所以有很多计算尝试计算输出变量的导数,所以输出变量对某个变量的导数,我们就用dvar命名,所以在很多计算中你需要计算最终输出结果的导数,在这个例子里是J,还有各种中间变量,比如a、b、c、u、v。
当你在软件里实现的时候,变量名叫什么?
你可以做的一件事是,在python中,你可以写一个很长的变量名,比如dFinalOutputvar_dvar,但这个变量名有点长,我们就用dJ_dvar,但因为你一直对dJ求导,对这个最终输出变量求导。我这里要介绍一个新符号,在程序里,当你编程的时候,在代码里,我们就使用变量名dvar,来表示那个量。

好,所以在程序里是dvar表示导数,你关心的最终变量J的导数,有时最后是L,对代码中各种中间量的导数,所以代码里这个东西,你用dv表示这个值,所以dv=3,你的代码表示就是da=3。
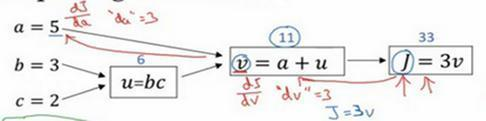
好,所以我们通过这个流程图完成部分的后向传播算法。我们在下一张幻灯片看看这个例子剩下的部分。
我们清理出一张新的流程图,我们回顾一下,到目前为止,我们一直在往回传播,并计算d





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 456
456

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










