数据结构--二叉树

什么是二叉树？

二叉树就是每个节点最多只有两个节点的树就叫二叉树。

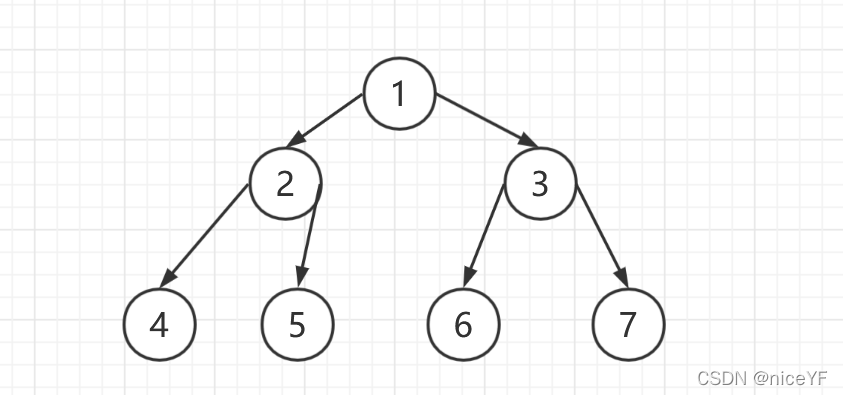
就像这样

1.递归过程：

递归序：从上往下，从左往右进行遍历的方式，所经过的节点的顺序。例如上图中。

先经过1，再经过2，到达4，

4到左孩子发现没有了，回到4，然后去右孩子，发现也没有再回到4

按照这种方式依次经过的顺序为 1 2 4 4 4 2 5 5 5 2 1 3 666 3 777 3 1.

每一个节点都要经过三次。

如果在第一次经过的时候就输出节点，那就是先序遍历。也就是根左右

如果在第二次经过的时候输出节点，那就是中序遍历。第一次经过是输出了左节点，然后才是根节点，最后是右节点。左根右。

如果在第三次经过的时候输出节点，那就是后序遍历。左右根。

package com.yf;

public class Day14 {
	
	public static void main(String[] args) {
		NodeTwo node = new NodeTwo(1);
		node.left = new NodeTwo(2);
		node.right = new NodeTwo(3);
		node.left.left = new NodeTwo(4);
		node.left.right = new NodeTwo(5);
		node.right.left = new NodeTwo(6);
		node.right.right = new NodeTwo(7);
//		preOrderRecur(node);
//		inOrderRecur(node);
		posOrderRecur(node);
		
	}
	
	
	
	public static void f(NodeTwo node) {
		//第一次进入节点
		if(node == null) {
			return ;
		}
		f(node.left);
		//从left出来后第二次进入节点
		f(node.right);
		//从right出来后第三次进入节点
	}
	public static void preOrderRecur(NodeTwo node) {
		//先序遍历
		if(node == null) {
			return ;
		}
		System.out.println(node.value);
		preOrderRecur(node.left);
		preOrderRecur(node.right);
		
	}
	public static void inOrderRecur(NodeTwo node) {
		//中序遍历
		if(node == null) {
			return ;
		}
		inOrderRecur(node.left);
		System.out.println(node.value);
		inOrderRecur(node.right);
	}
	public static void posOrderRecur(NodeTwo node) {
		//后续遍历
		if(node == null) {
			return ;
		}
		posOrderRecur(node.left);
		posOrderRecur(node.right);
		System.out.println(node.value);
		
	}
}

class NodeTwo{
	public int value;
	public NodeTwo left;
	public NodeTwo right;
	public NodeTwo(int value) {
		this.value = value;
	}
	
	
}

2.非递归过程

先序遍历：打印顺序是头左右

压入栈中的顺序是头右左。

先把根节点压入栈中。

然后循环以下操作{

弹出一个节点，打印（栈中没有节点了就结束）

如果有右节点，先压入右节点

然后如果有左节点压入左节点。

}

	public static void preOrderUnRecur(NodeTwo node) {
		Stack<NodeTwo> stack = new Stack<NodeTwo>();
		stack.add(node);
		while(!stack.isEmpty()) {
			NodeTwo head = stack.pop();
			System.out.println(head.value);
			if(head.right!=null) {
				stack.add(head.right);
			}
			if(head.left!=null) {
				stack.add(head.left);
			}
			
		}
		
	}

}

后序遍历：

先序压入栈中的顺序是头右左，

如果我们将压入栈中的数据线不打印而是继续压入到另外一个栈里面，那么在另外一个栈里面的顺序是不是就变成了左右头，也就是后序遍历。

定义两个栈 栈1 栈2

先头节点入栈1

然后循环{

栈1 中弹出一个节点，这个节点存到栈2中去

然后压入左节点

再压入右节点

因为先压左再压右弹出时就是先弹右再弹左，存到栈2中的就是根右左。

弹出的时候就是左右跟（后序）.

}

	public static void posOrderUnRecur(NodeTwo node) {
		Stack<NodeTwo> stack = new Stack<NodeTwo>();
		Stack<NodeTwo> stackCopy = new Stack<NodeTwo>();
		stack.add(node);
		while(!stack.isEmpty()) {
			NodeTwo head = stack.pop();
			stackCopy.add(head);
			if(head.left!=null) {
				stack.add(head.left);
			}
			if(head.right!=null) {
				stack.add(head.right);
			}
		}
		while(!stackCopy.isEmpty()) {
			NodeTwo nodeTwo = stackCopy.pop();
			System.out.println(nodeTwo.value);
		}
		
	}

}

中序遍历：

先把树所有的左节点从上到下压入栈中

弹出一个节点，并打印，看这个节点是否有右子树，

如果有就再把这棵子树所有的左节点压入栈中，周而复始。

压入栈中的顺序是中左，所以弹出的顺序是左中，

弹出中之后去右边进行压栈和弹出，所以顺序就是左中右

右边不断分解成左中

其实就是左中左中左中左中。。。。。。

	public static void inOrderUnRecur(NodeTwo node) {
		if(node != null) {
			Stack<NodeTwo> stack = new Stack<NodeTwo>();
			while(!stack.isEmpty()|| node!=null) {
				if(node!=null) {//如果这个节点不为空，就把左边的全部进栈
					stack.push(node);
					node = node.left;
				}else {
					node = stack.pop();//如果为空就从栈中弹出一个节点
					System.out.println(node.value);//在每次弹出节点的时候都打印节点
					node = node.right;//弹出之后对右边子树进行同样的操作。循环。
					
				}
			}
		}