LSTM梯度问题

        在LSTM之前，RNN（循环神经网络）在使用过程中经常会出现梯度爆炸与梯度消失，这将大大影响了数据的计算与模型的稳定性。后来人们发现，LSTM很好地解决了这个缺点。那么LSTM是如何解决有关梯度问题的呢？让我们来看看——

        首先，我们先要弄清楚什么是梯度消失和梯度爆炸。梯度，可以理解为导数值。根据一般的神经网络，我们能够大体上得到关于输入输出的表达式：

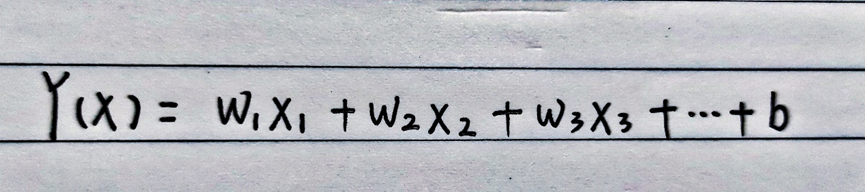
        在正常情况下，我们通过输入一组数据，经过该表达式就能得到一组输出。

        那么在具有反馈的神经网络中，如何通过一组输出，找到影响误差的某个权重呢？这就涉及到导数了。以ω1为例，我们可以通过以下方式从输出值反过来得到ω1 ：

        其中，ω1就是一个梯度。梯度消失，指的是导数值=0；而梯度爆炸，则指导数值——>∞。    

        那么这两种情况是如何影响模型的稳定性的呢？想想看，当某个权值为0，该权值对输出来说就没有任何贡献，也就是说在利用反馈来调整权值时没有起到作用；反之，当某个权值趋近于∞，对误差的调整作用过大，严重影响了整个模型的稳定性。

        现在，我们来看看这两大问题在LSTM中是怎样被解决掉的：

        在传统的RNN中，有四大原理公式：

        对于梯度W而言，我们需要通过链式法则求导，如下：

        其中，

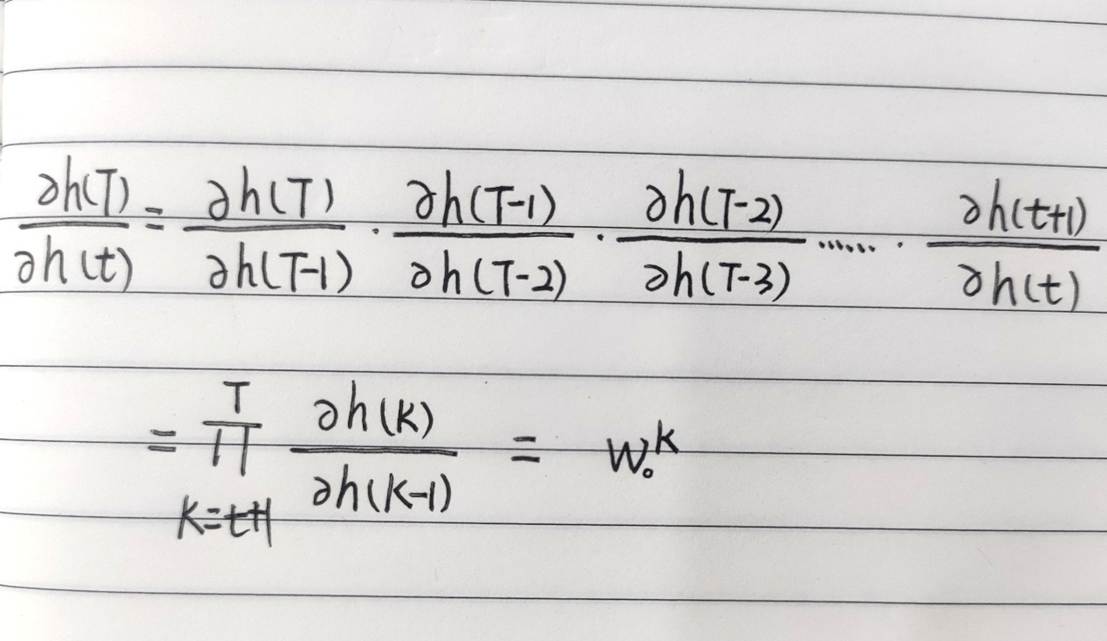
        在这里，其实还涉及到tanh归一化，不过归一化的本质就是：最后一个ω越接近于0的话，越化越接近于0；反之，越化越接近于1。我们不妨把它们都看作是相同的一个数W0,便于理解原理。

        接下来我们可以看到，在求解W时，我们遇到了一个k次幂，当最后一个ω<1，经过k次幂就为0；反之，当最后一个ω>1,经过k次幂就为∞。

        这就是RNN容易出现梯度消失的原因。接下来，我们来看看LSTM如何解决上述梯度问题——

        在LSTM中，有7大基本公式：

        我们仍然选取：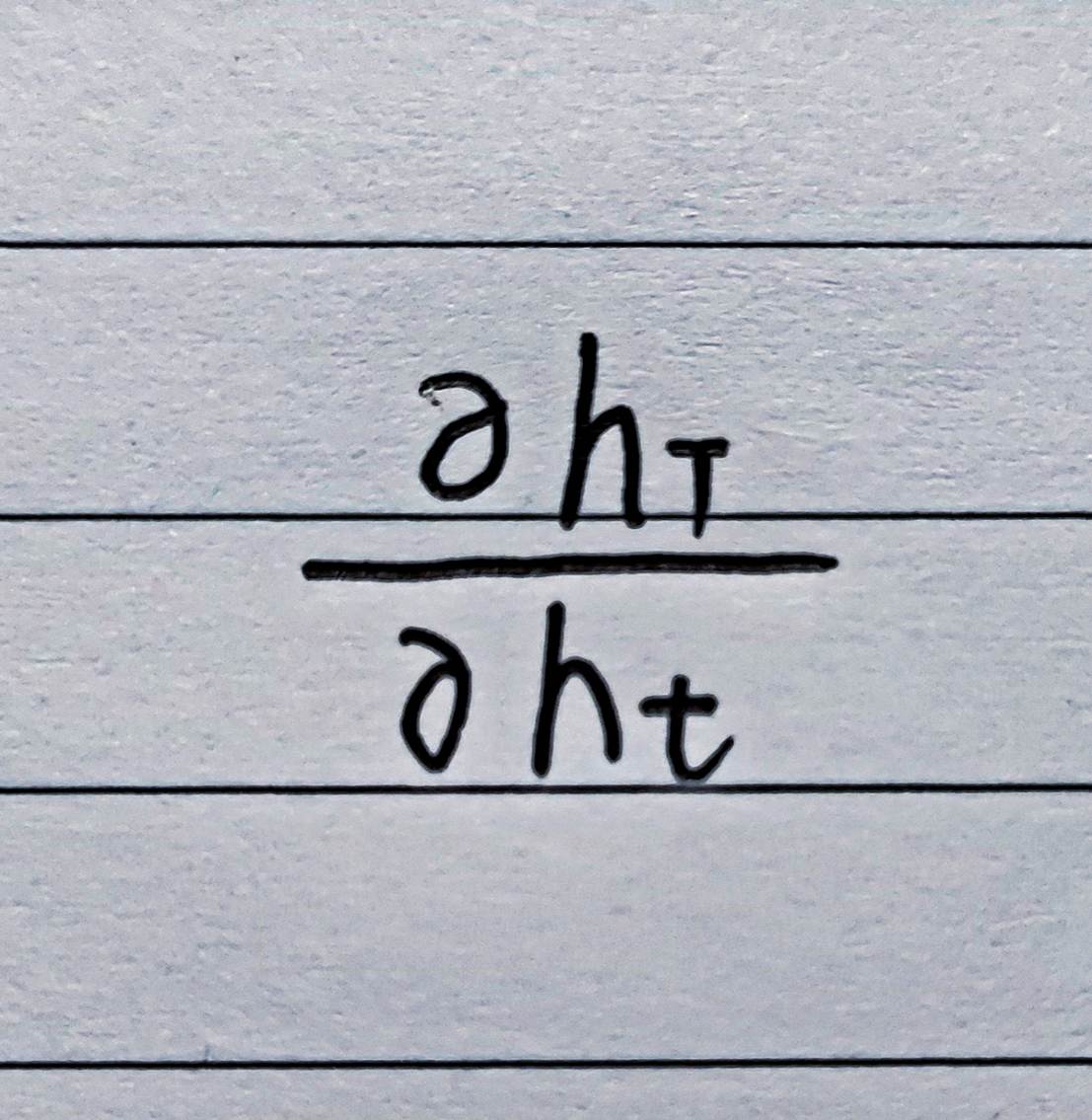

        在这里，我们可以用Ct来代替，得到如下式子：

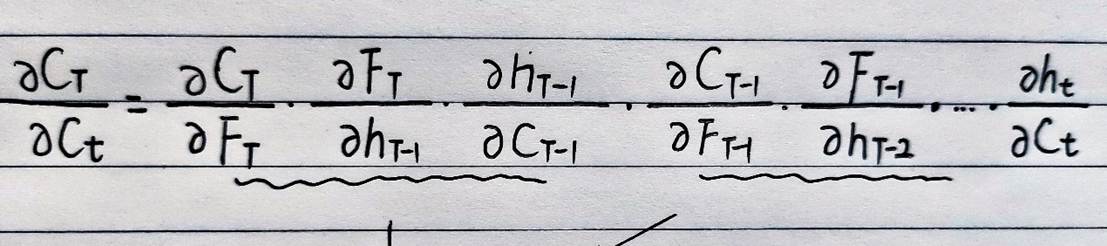
        然后，我们可以继续利用链式法则，将每三项进行合并，得到以下式子：

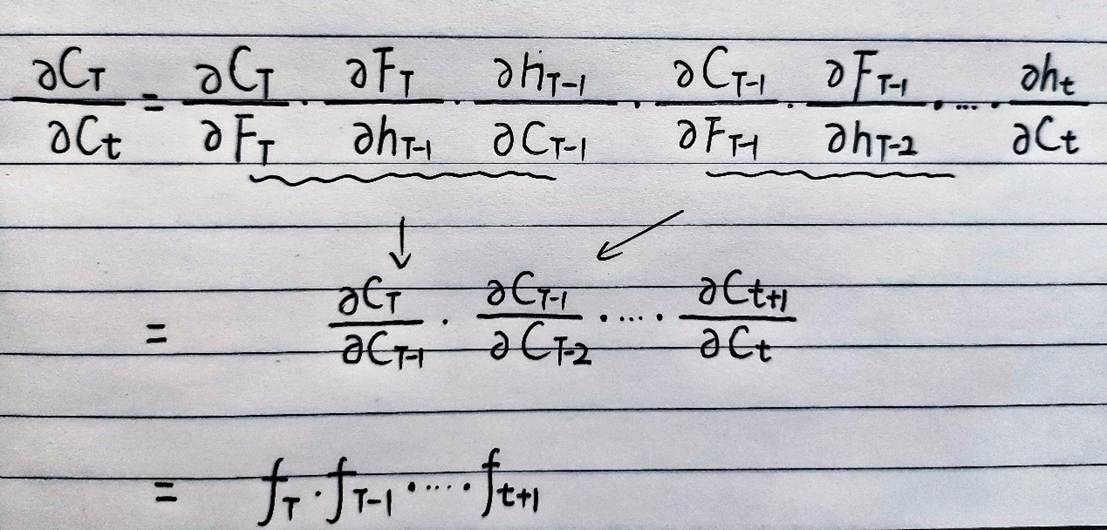
        其中，Ft对整个式子的影响是最大的，也就是遗忘门这一项：

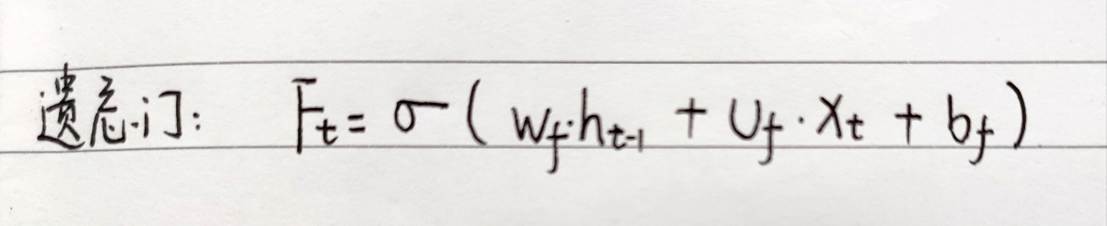
        于是，对于某梯度的求解转变为了对遗忘比重的分析：

        在每一个时间步里，Ft的值都是不一样的，这就很好地避免了指数型变化，也就有效解决了大部分梯度消失与梯度爆炸问题。

        那有人可能会发问：“如果Ft较多取0或取1怎么办？不还是会发生梯度问题吗？”

        这就得从遗忘门的职能出发进行理解了——

        遗忘门取值在【0，1】，这对梯度的求解提供了一套很强的逻辑：当FT取值接近1时，说明历史信息对预测输出很重要，梯度保留；当FT取值接近0时，说明该历史信息对预测输出来说没有用处，这时候就算梯度消失也无济于事。

        综上，LSTM通过遗忘权重有效解决了RNN遗留的梯度消失与梯度爆炸问题。

PS:如果觉得我讲解得还行的话，可以给我个支持与鼓励，欢迎关注我，后续内容会偏向电力电子部分，希望能给大家带来帮助，我们一起加油！！！