数字信号处理——窗函数

使用Python进行信号处理：窗函数的应用

最新推荐文章于 2025-09-11 02:30:25 发布

原创最新推荐文章于 2025-09-11 02:30:25 发布 · 3.7k 阅读

16 ·

CC 4.0 BY-SA版权

文章标签：

#python #数据分析 #信号处理

DSP 专栏收录该内容

2 篇文章

订阅专栏

本文介绍了如何使用Python的scipy.signal库中的窗函数，特别是hann窗，来减少FFT数据截取的跳变。通过示例展示了hann窗的特性，包括其对称性对周期信号的影响，以及如何通过sym参数解决连续0值问题。同时，解释了窗函数与信号乘积后对频谱能量分布的影响，以及如何保持信号能量不变。

本文内容和程序来自参考书《Python科学计算》

为了减少FFT所截取的数据段前后的跳变，可以对数据先乘以一个窗函数，使得其前后数据能平滑过渡。例如常用的hann窗函数的定义如下：
在这里插入图片描述
其中N为窗函数的点数，下面是一个512点hann窗的曲线：

>>> import pylab as pl
>>> import scipy.signal as signal
>>> pl.figure(figsize=(8,3))
>>> pl.plot(signal.hann(512))

窗函数都在scipy.signal库中定义，它们的第一个参数为点数N。可以看出hann窗函数是完全对称的，也就是说第0点和第511点的值完全相同，都为0。在这样的函数和信号数据相乘的话，结果中会出现前后两个连续的0，这样FFT的结果所表示的周期信号中有两个连续的0值，会对信号的周期性有一定的影响。

-计算周期信号的一个周期的数据

考虑对一个正弦波取样10个点，那么第一个点的值为0，而最后一个点的值不应该是0，这样这10个数据的重复才能是精确的正弦波，下面的两种计算中，前者是正确的：

>>> np.sin(np.arange(0, 2*np.pi, 2*np.pi/10))
array([  0.00000000e+00,   5.87785252e-01,   9.51056516e-01,
         9.51056516e-01,   5.87785252e-01,   1.22464680e-16,
        -5.87785252e-01,  -9.51056516e-01,  -9.51056516e-01,
        -5.87785252e-01])
>>> np.sin(np.linspace(0, 2*np.pi, 10))
array([  0.00000000e+00,   6.42787610e-01,   9.84807753e-01,
         8.66025404e-01,   3.42020143e-01,  -3.42020143e-01,
        -8.66025404e-01,  -9.84807753e-01,  -6.42787610e-01,
        -2.44929360e-16])

为了解决连续0值的问题，hann函数提供了一个sym关键字参数，如果设置其为0的话，那么将产生一个N+1点的hann窗函数，然后取其前N个数，这样得到的窗函数适合于周期信号：

>>> signal.hann(8)
array([ 0.        ,  0.1882551 ,  0.61126047,  0.95048443,  0.95048443,        0.61126047,  0.1882551 ,  0.        ])
>>> signal.hann(8, sym=0)
array([ 0.        ,  0.14644661,  0.5       ,  0.85355339,  1.        ,        0.85355339,  0.5       ,  0.14644661])

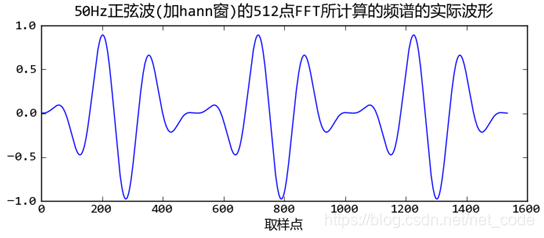
50Hz正弦波与窗函数乘积之后的重复波形如下：

>>> t = np.arange(0, 1.0, 1.0/8000)
>>> x = np.sin(2*np.pi*50*t)[:512] * signal.hann(512, sym=0)
>>> pl.plot(np.hstack([x,x,x]))
>>> pl.show()

加hann窗的50Hz正弦波的512点FFT所计算的实际波形
回到前面的例子，将200Hz, 300Hz的叠加波形与hann窗乘积之后再计算其频谱，得到如下频谱图：
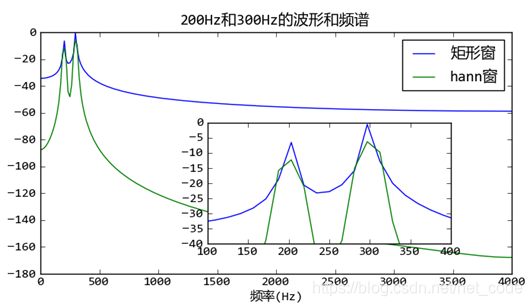
在这里插入图片描述
可以看到与hann窗乘积之后的信号的频谱能量更加集中于200Hz和300Hz，但是其能量有所降低。这是因为hann窗本身有一定的能量衰减：

>>> np.sum(signal.hann(512, sym=0))/512
0.5

因此如果需要严格保持信号的能量的话，还需要在乘以hann窗之后再乘以2。