第4章 电动汽车和混合动力汽车的传动架构与拓扑设计
4.1 引言
4.1.1 电动汽车架构
对于电动汽车(EV),电机被用作动力源来驱动车辆。根据电机的构型,可分为四种构型:单电机驱动、双电机独立驱动、轮毂电机驱动和双电机前后轴独立驱动。
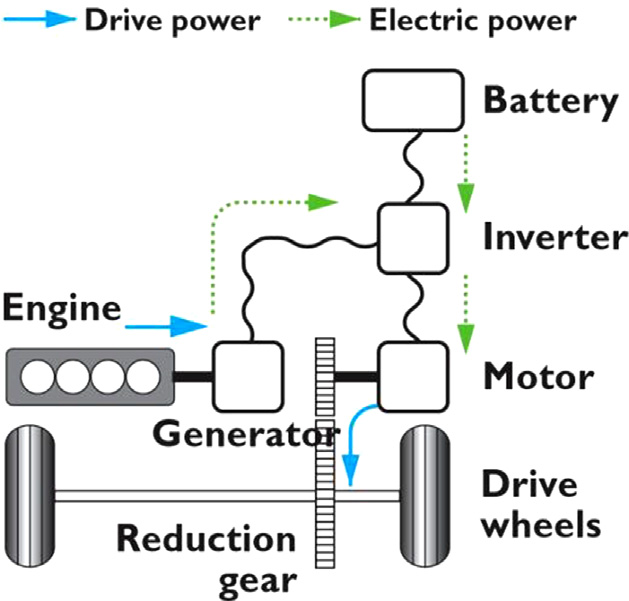 展示了单电机驱动的构型,其中电机替代了发动机,且保留了差速机构。
展示了单电机驱动的构型,其中电机替代了发动机,且保留了差速机构。
 展示了双电机独立驱动的构型,与单电机驱动相比,取消了差速机构,因此传动机构得以简化。
展示了双电机独立驱动的构型,与单电机驱动相比,取消了差速机构,因此传动机构得以简化。
 展示了轮毂电机驱动的构型,其扭矩分配更加灵活,从而实现了优异性能。
展示了轮毂电机驱动的构型,其扭矩分配更加灵活,从而实现了优异性能。
 展示了前后轴电机独立驱动的构型。
展示了前后轴电机独立驱动的构型。
4.1.2 混合动力汽车架构
通常,混合动力汽车可粗略分为三种类型:并联式、串联式和分流式。在这三种类型中,功率分流式最为流行。这主要是因为功率分流式混合动力汽车中的发动机与车速解耦,即使大部分功率流经机械路径,发动机仍可高效运行(
 )。
)。
4.1.2.1 串联混合动力
在串联混合动力系统中,内燃机驱动一台电动发电机(通常为三相交流发电机加整流器),而不是直接驱动车轮。电动机(EM)是向车轮提供动力的唯一方式。该发电机既为电池充电,又为驱动车辆的电动机供电。当需要大量功率时,电动机会从电池和发电机同时获取电能。串联式混合动力系统可由超级电容器(或飞轮)辅助,通过减少电池中的能量损耗来提高效率。它们在加速时提供峰值能量,在制动时利用再生能量。因此,超级电容器在低速时保持充电状态,在高速时几乎放空。此外,电池的深度循环被减少,从而降低了电池的应力。
由于电动机在宽速度范围内效率较高,因此电机与车轮之间不需要复杂的传动系统。
串联混合动力汽车(HVs)的一些缺点包括:内燃机(ICE)、发电机和电动机(EM)需要能够处理车辆的全部功率,因此动力总成的总重量、成本和尺寸可能过大。来自内燃机的功率必须经过发电机和电动机传输。在长途高速公路驾驶时,由于需要进行多次能量转换,整体效率低于传统传动系统。
串联式混合动力汽车的一些优势包括:内燃机与车轮之间没有机械连接。发动机‐发电机组可以安装在任意位置。无需传统的机械传动部件(如变速箱和传动轴),并且可以轻松实现独立的轮毂电机。即使车辆速度变化,内燃机仍可在较窄的转速范围(即其最高效的工作范围)内运行。串联式混合动力在启停式城市驾驶过程中效率最高。
4.1.2.2 并联混合动力
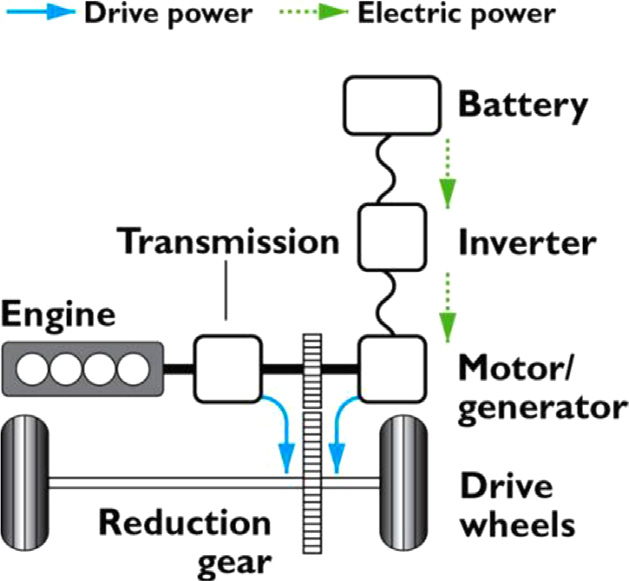
并联混合动力系统同时将内燃机和电机以并联方式连接到机械传动系统。大多数设计将大型发电机和电机组合成一个单元,通常位于发动机和传动系统之间,取代传统的启动电机和交流发电机(参见前面所示的图示)。电池可以在再生制动期间以及巡航期间(当内燃机输出功率高于推进所需功率时)进行充电。由于存在车轮与电机之间为固定机械连接(无离合器),当汽车不移动时,电池无法充电。
当车辆仅使用电力牵引动力,或在制动进行能量回收时,内燃机不工作(通过离合器断开)或未被供能(以空转方式旋转)。
有时会使用额外发电机。在这种情况下,车辆不行驶时电池可以充电,且内燃机与传动系统断开运行。然而,与混合动力汽车相比,该系统的重量和成本增加(
 )。
)。
并联式混合动力汽车的一些缺点如下:它们采用了一套较为复杂的系统。内燃机不在狭窄或恒定的转速范围内运行,因此在低转速时效率下降。由于内燃机与车轮未解耦,车辆在静止状态时无法为电池充电。
并联式混合动力汽车的一些优势包括在巡航和长途高速公路驾驶期间总效率更高。与串联式混合动力相比,可在电动机和内燃机动力之间更灵活地切换。由于电动机仅用于辅助牵引,因此其功率设计可以小于内燃机,并且只需要一个电机/发电机。
4.1.2.3 混联式混合动力
混联式混合动力系统具有串联和并联混合动力系统的特性。发动机与驱动桥之间存在机械和电气双重连接。这种分功率路径允许机械功率和电功率相互结合,但会带来一定的复杂性成本。
功率分流装置被集成在动力总成中。传递至车轮的功率可以是机械的、电的,或两者兼有。并联混合动力系统也是如此。然而,该组合系统的主要原理在于将发动机提供的功率与驾驶员需求的功率进行解耦。
在传统车辆中,为满足从静止状态加速的需求,所使用的发动机通常比匀速巡航所需的动力系统更大。这是由于内燃机在低转速时扭矩最小,因为发动机本身就是一个空气泵。而电动机在静止时可输出最大扭矩,因此非常适合弥补发动机在低转速时的扭矩不足。
在混联式混合动力系统中,可以采用更小、灵活性较低但效率更高的发动机,这种发动机通常是传统奥托循环的变体,例如米勒或阿特金森循环。这显著提高了车辆的整体效率,而再生制动的作用相对较小。
4.2 电动汽车和混合动力汽车架构表示
4.2.1 简图
为了便于分析,通常使用简图来表示传动系统。单行星齿轮组的简图如
 所示,该图展示了通用三模式混合动力系统的传动机构的简图。
所示,该图展示了通用三模式混合动力系统的传动机构的简图。
4.2.2 杠杆类比图
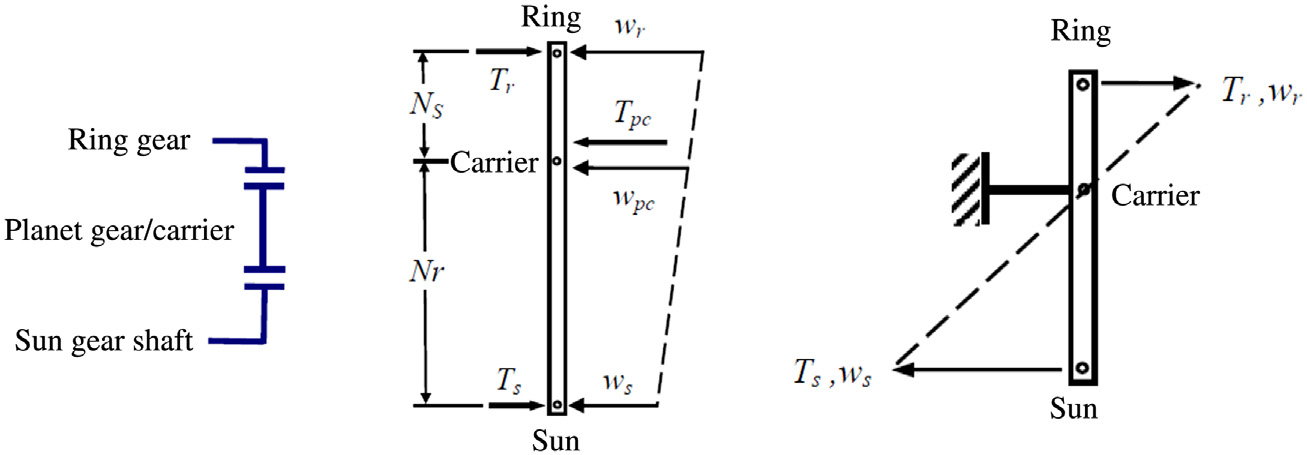
在机械运动学与动力学中,一种称为杠杆类比图的更简单方法被广泛用于工业中分析和表征齿轮系。当分析具有两个以上连接行星齿轮的齿轮系时,杠杆类比图非常有用。
齿轮组。对于单行星齿轮组,无需添加抽象层级。杠杆类比是行星齿轮旋转部件的平移系统表示。在杠杆类比中,整个复合行星齿轮系通常可用单个垂直杠杆表示。输入、输出和反作用力矩由作用在杠杆上的水平力表示。杠杆相对于反作用点的运动代表旋转速度。
通过使用杠杆,例如,可以直观地理解传动系统的本质功能,而无需涉及行星齿轮运动学的复杂性。
建立行星齿轮组的杠杆系统类比的步骤如下:(1)用垂直杠杆替换每个齿轮组;(2)根据齿轮组的互连关系对杠杆进行重新缩放、互连和/或合并;(3)根据齿轮组的连接确定与杠杆的连接。杠杆是替代行星齿轮组的类比基本构件。杠杆比例由太阳轮和齿圈的齿数决定。接下来的步骤是合并杠杆并识别齿轮组中的连接。
单行星齿轮组的简图如
 所示,其杠杆替换如
所示,其杠杆替换如
 所示。力矩方程通过杠杆图推导得出。这些替换的依据可能并不明显,但杠杆的水平力与速度关系可视为等同于齿轮组的力矩与旋转速度关系。如
所示。力矩方程通过杠杆图推导得出。这些替换的依据可能并不明显,但杠杆的水平力与速度关系可视为等同于齿轮组的力矩与旋转速度关系。如
 所示,当简单齿轮组的行星架接地时,齿圈和太阳轮以相反方向旋转,速度与齿数成反比,类比杠杆上的对应点也表现出相同的行为。
所示,当简单齿轮组的行星架接地时,齿圈和太阳轮以相反方向旋转,速度与齿数成反比,类比杠杆上的对应点也表现出相同的行为。
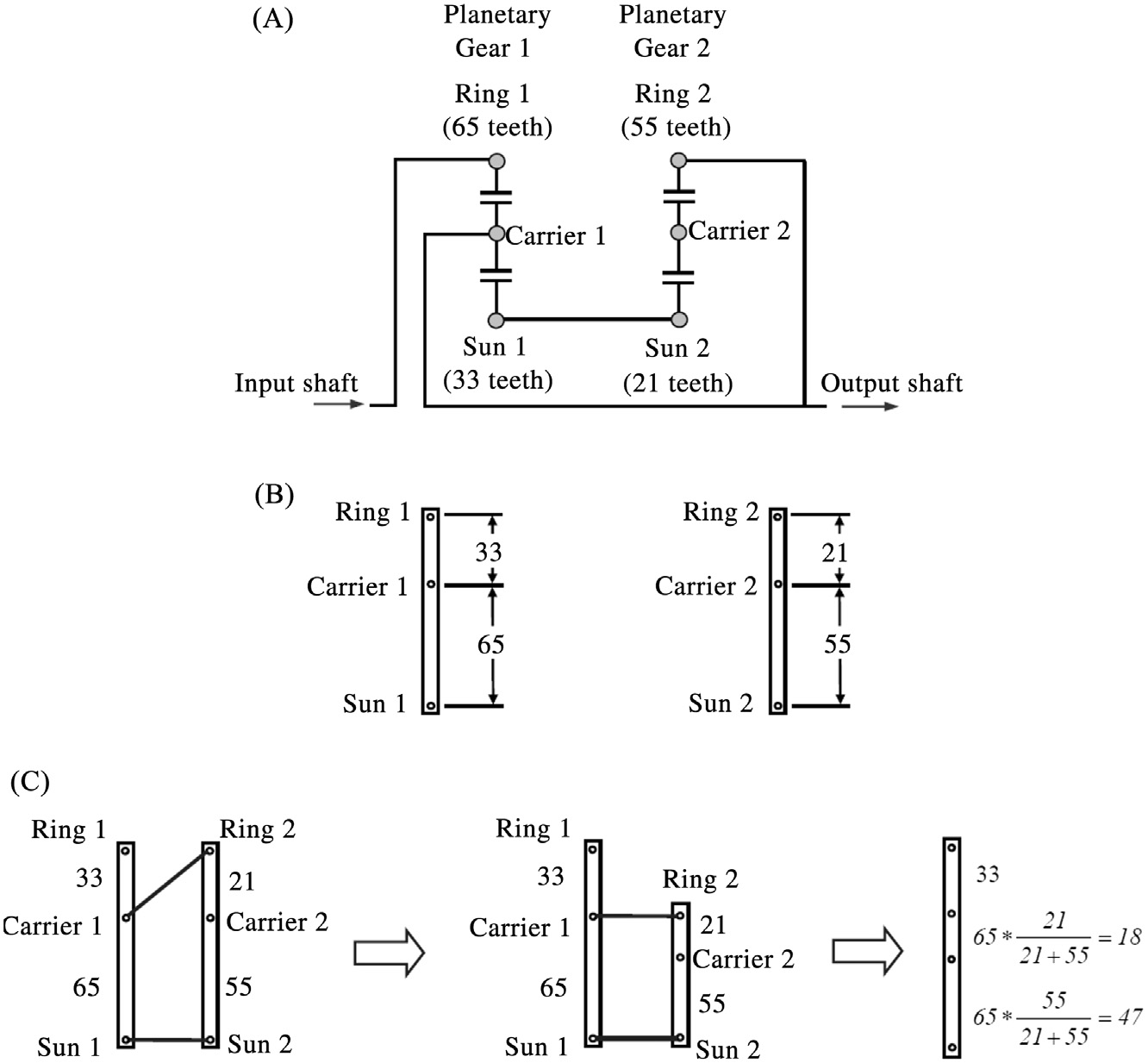
齿轮组之间的互连被替换为连接到杠杆相应位置的水平连接杆。当两个齿轮组有一对互连时,其对应的杠杆的相对比例常数和位置必须使得互连的连杆保持水平。通过一对水平连接杆相连的杠杆始终保持平行,因此在功能上可用一个具有相同点间垂直尺寸的单个杠杆替代。这一点在图4.1中进行了说明,其中杠杆代表了两个简单的行星齿轮组。设行星齿轮1的齿圈和太阳轮齿数分别为65和33;行星齿轮2的齿圈和太阳轮齿数分别为55和21。
 显示了这两个行星齿轮组的简图,
显示了这两个行星齿轮组的简图,
 显示了两个杠杆表示,而
显示了两个杠杆表示,而
 展示了两个杠杆合并的过程。
展示了两个杠杆合并的过程。
杠杆类比法可以简便地分析机械传动系统的角速度和扭矩。应遵循以下步骤:(1)用等效杠杆替换行星齿轮组;(2)重新缩放杠杆,使其互连部分保持水平;(3)在可能的情况下组合杠杆;(4)确定每个齿轮的输入、输出和反应;(5)分别求解杠杆系统的角速度和扭矩。
4.2.3 图表示
行星传动机构的图模型主要分为两种类型。第一种类型以行星齿轮系作为基本拓扑单元,以连杆和运动副作为基本元素。
 展示了基本拓扑单元的图表示。顶点和线分别表示连杆以及连杆之间的连接,粗线表示齿轮副,细线表示转动副。该模型来自布赫斯鲍姆和弗赖登斯坦(
展示了基本拓扑单元的图表示。顶点和线分别表示连杆以及连杆之间的连接,粗线表示齿轮副,细线表示转动副。该模型来自布赫斯鲍姆和弗赖登斯坦(
 4.12)。
4.12)。
第二种类型使用行星齿轮系作为基本拓扑单元。每个行星齿轮系仅包含三个基本连杆:太阳轮、行星架和齿圈(在此图模型中不考虑行星轮)。针对此类模型已提出了多种表示方法。这种模型的优点是将行星齿轮系作为基本拓扑单元,从而简化了图论。
4.3 功率分流式混合动力汽车的拓扑设计
一般来说,混合动力汽车可根据其设计特点分为三类,即串联式、并联式和功率分流式串联 并联式,各类均有其优势,具体内容将在后续章节中进一步讨论。在串联混合动力系统中,内燃机驱动发电机而不是直接驱动车轮,电动机是唯一向车轮提供动力的动力源。
串联式混合动力汽车的优点在于没有机械内燃机与车轮之间没有直接的机械连接,因此内燃机可以在其最高效的范围内运行。然而,串联式混合动力汽车的缺点是来自内燃机的功率必须经过发电机和电动机,从而导致效率较低,并且动力总成的总重量、成本和尺寸可能过大。并联混合动力系统将内燃机和电动机并联连接到机械传动系统。与串联式混合动力相比,由于电动机仅用于辅助牵引,因此可设计为比内燃机功率更小,且只需要一个电机/发电机。然而,该系统较为复杂,并且由于内燃机未与车轮解耦,因此在静止状态下无法为电池充电。通过使用动力分配装置,电动机可以像串联式混合动力一样将来自电池或发动机的功率传递给车辆,同时发动机也可以像并联式混合动力一样直接驱动车辆。这种设计可以兼顾并联式和串联式的优点,并避免它们的缺点。
4.3.1 图模型与拓扑综合方法
在行星传动机构中,行星齿轮由四部分组成:太阳轮、行星架、齿圈和行星轮。行星轮的作用是将太阳轮、行星架和齿圈连接在一起,不能作为外部部件用于动力输出。因此,行星齿轮系可以简化为仅包含太阳轮、齿圈和行星架。
行星传动机构通常由输入(发动机、电机)、输出、制动器和行星齿轮系组成。由于图论已成功用于表示与功能分离的传动系统拓扑结构,因此建立了如所示的综合图模型。在该图模型中,顶点1、3n12、3n13 和 3n14 分别表示发动机、电机、输出和框架;顶点 2 2 3n11 表示行星部件。
本章中图模型的具体特征如下:
1. 在图模型中,为了描述模块之间的关系,模块包括由顶点表示的行星齿轮系(PGTs)和反应元件。PGT的模块关系由粗边表示, PGT之间的固定连接由虚线边表示。
2. 根据功能,行星齿轮系可分为两部分。一部分是模块以及行星齿轮系之间的固定连接,以及
3. 为了简化行星齿轮系的自动绘图,将行星齿轮系的模块分为三层:上行对应齿圈,中行对应行星架,下行对应太阳轮。
在图论模型中,采用加权图的方法,即对连接进行加权,以区分来自不同部件的连接。物理连接定义了每条边的权重及相应的模型,如表4.1所示。
因此,两自由度(2‐DOF)行星齿轮系候选结构的综合包括两个步骤。第一步,确保行星齿轮系之间的固定连接。第二步,在确定固定连接后,行星齿轮系的模块应与反应元件连接。在此步骤中,使用杠杆图以避免同构结构。在2‐DOF
| 齿圈层 | 2 5 8 3n–1 |
|---|---|
| 行星架层 | 3 6 9 3n |
| 太阳轮层 | 4 7 10 3n+1 |
| ...... | |||||||||||
| ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... | |
| ...... | |||||||||||
| 行星齿轮系,行星齿轮系的数量与自由度之间的关系可以表示为: | |||||||||||
| N5 2P2 F (4.1) | |||||||||||
| 其中,P、F 和 N 分别表示该方案的行星齿轮系数量、固定连接数量和自由度数量。当选定自由度数量和行星齿轮系数量时,即可得到固定连接的数量。 |
4.3.2 递归算法
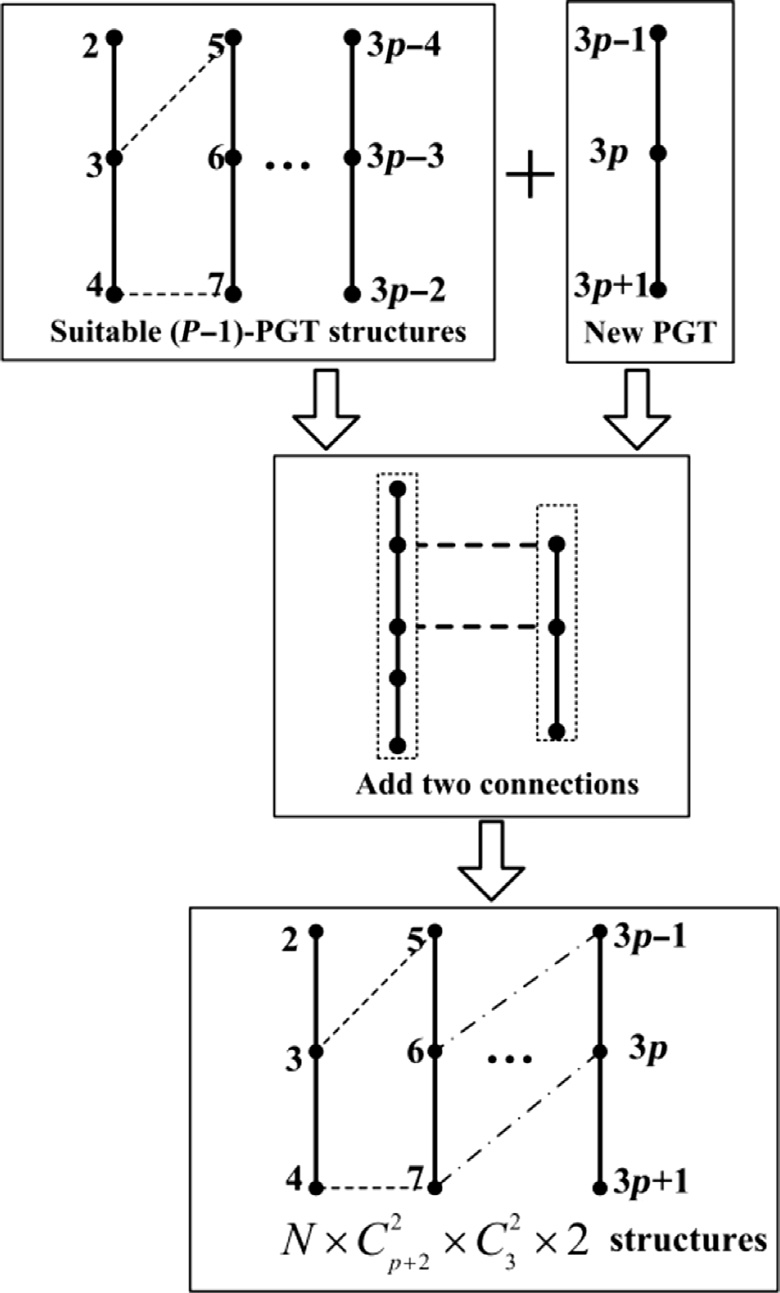
显示了一个三行星齿轮系结构的示意图截面。在此结构中,三个行星齿轮系通过四个固定连接组合在一起,然后将输入、输出以及三个制动器分别连接到行星齿轮系的相应部件。由于图论已成功用于表示与功能分离的拓扑结构,因此可建立如 所示的综合图模型。
如果给定行星齿轮系的数量,则可通过应用综合方法推导出所有行星齿轮系与外部部件的可能组合。结果得到双行星齿轮系有 216 种构型,三行星齿轮系有 12960 种构型。对于四行星齿轮系,有 1749600 种可能构型。由于四行星齿轮系的构型数量较大,在设计传动系统时会导致较长的计算时间和较低的设计效率。
在选择合适方案时,满足特定功能的速比作为已知条件给出。可以理解为双行星齿轮系的速比包含在三行星齿轮系的速比中,因为速比之间的数学关系已经确定。通过分析速比的功率流,这些速比可由一个或多个行星齿轮系实现,如 和 所示。由于传动效率与齿轮啮合损失相关,更多的齿轮啮合将导致更多的功率损失并降低传动效率。从这一角度来看,速比应通过较少的行星齿轮系来实现。对于三行星齿轮系方案,若三个速比均由一个行星齿轮系实现,则该方案效率最高。然而,每个行星齿轮系都需要连接输入和输出,这会因功率循环而降低效率。因此最常见的速比形式是三速比,分别由一个行星齿轮系、双行星齿轮系和三行星齿轮系实现。通过提高机构复用率来增加速比数量,符合设计意图。
比较 与 的功率流,可以看出三行星齿轮系中的两种三速比形式与双行星齿轮系中的两速比形式相同。由于 P 速比是在 P 行星齿轮系的两自由度中推导得出的,因此提出一个假设:给定的 P21 个速比包含在给定的 P 速比中,其中 P21 个速比和 P 个速比是推导两自由度构型的条件,而 P 为速比数量。然后,在分析方案的功率流和传动效率的基础上,提出了演绎方法,即以两自由度的(P21)行星齿轮系合适方案作为基础结构,包含于合适的 P 行星齿轮系结构中。通过向合适的(P21)行星齿轮系方案添加一个行星齿轮系,可生成 P 行星齿轮系的拓扑结构。该演绎方法的算法如 所示,其中 N 表示(P21)行星齿轮系合适方案的数量。
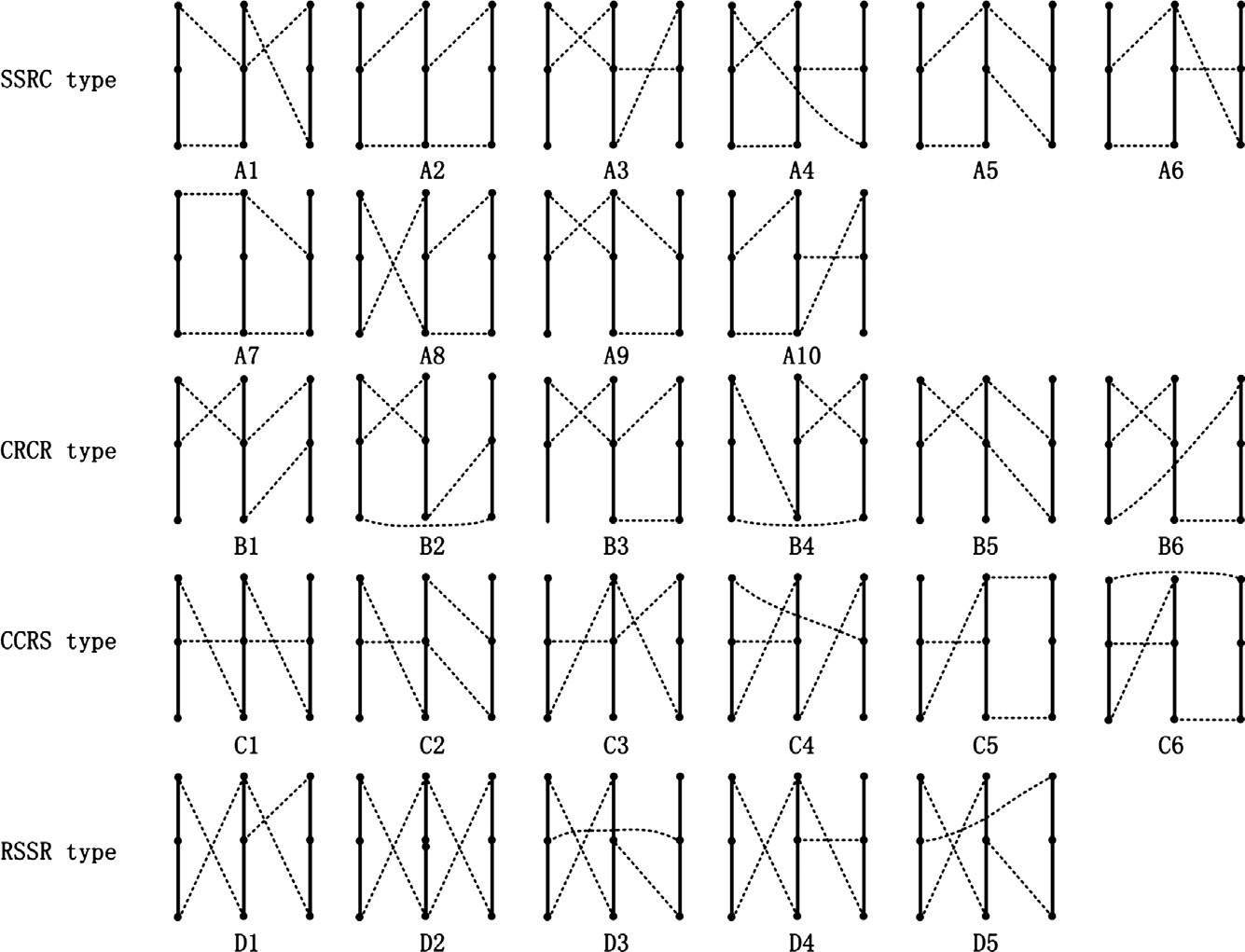
通过枚举法生成了12,960个方案,而通过演绎方法仅生成了 2,880 个方案。通过比较两种方法生成的方案数量,演绎方法可以大幅减少候选方案的数量。应用演绎方法时,选出了27种三行星齿轮系的合适构型,如 所示。
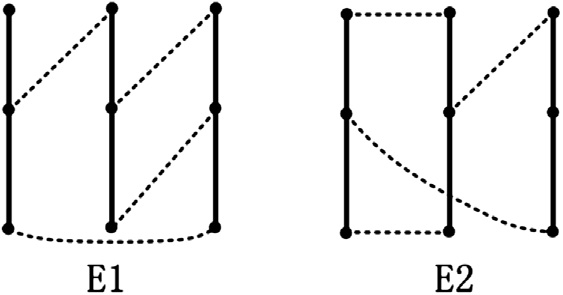
演绎方法选出的所有合适方案均包含在枚举方法得到的方案中。然而,存在两个冗余构型,如 所示。通过分析这两个构型的功率流,明显看出拓扑结构中的三个行星齿轮系有三个速比,从效率角度来看并非良好构型。此外,拓扑结构E2包含相同的模块连接,会因功率循环而降低效率。因此,这两个冗余构型在效率方面并不优越()。
4.3.3 运动学与动力学方程
在对机械和电气复合行星传动机构的速度和扭矩进行分析时,速度方程根据不同部件的连接类型分为三类:
-
行星齿轮系的方程
根据运动学与动力学分析,可得到各种行星机构组件的速度与扭矩关系:
$$
n_{S1} + k n_{R2} - (1 + k) n_C = 0 \quad (4.2)
$$
$$
T_S : T_R : T_C = 1 : k : -(1 + k) \quad (4.3)
$$ -
固定连接部件的方程
当两个部件通过固定连接或离合器连接时,其转速相等。因此,在通过图模型的邻接矩阵搜索传动机构的速度分析时,所使用的邻接矩阵元素值为1、3、5、6、8 和 101 n。各部件的速度与扭矩关系建立如下:
$$
n_i - n_j = 0 \quad (4.4)
$$
$$
T_i + T_j = 0 \quad (4.5)
$$
其中,i 和 j 表示邻接矩阵中的元素位于第二行第 j 列,且 i 列的部件相对于传动机构中的部件。
根据对行星齿轮系旋转速度和扭矩的分析与计算,可以得出各部件在不同工作模式下的运动状态,为机械和电气复合传动机构的设计提供了依据。
4.3.4 模式连接分析
对于可变结构的机电行星传动机构,在扩展过程中,自由度不仅输入和输出位置会发生变化,而且行星机构的连接形式也会改变。机构也将发生变化。通过分析每种工作模式的特性,多模式机电机构的设计由以下三个约束条件确定。
-
机械点升序条件
通过对分流特性的分析发现,输入分流模式和输出分流模式只能实现一个机械点,而复合分流模式可以实现两个机械点。通过控制离合器、制动器和电机工作状态,电‐机械复合行星传动机构可实现可变结构运行和多种工作模式。理论上,为了充分利用各种工作模式,可将各模式间的机械点作为模式切换点。综上所述,机械点可作为各种工作模式的特征参数,并可根据各工作模式下传动比的大小按升序排列机械点,以方便在机械点处进行模式切换。
如 所示,通过合并离合器和制动器的操作,理论上可以获得所有可能的工作模式,按升序排列可确定传动系统各工作模式速比的区间,并根据机械点尺寸进行判断。例如,C1 和 C2 是属于差速交换速度模式的两个相同点,D1 和 D2 属于同一工作模式,且存在区间重叠情况,导致这两种工作模式之间的机械模式切换点无法实现;而工作模式 E 的机械点与差速交换率模式的机械点 D2 重合,这两种工作模式可实现机械模式切换。因此,通过对各工作模式的机械点进行排序,可初步选定工作模式,并可结合机械点的模式切换进行设计。
-
离合器和制动器的逻辑顺序
在传动机构中,通过合并不同的离合器和制动器可以获得相同的工作模式。这意味着需要两种或更多种工作模式来满足特定的传动比范围。因此,必须从多模式连接的各种工作模式中选择特定的工作模式。
从工程应用的角度来看,控制元件的最佳操作是在相邻工作模式切换时才进行更换。
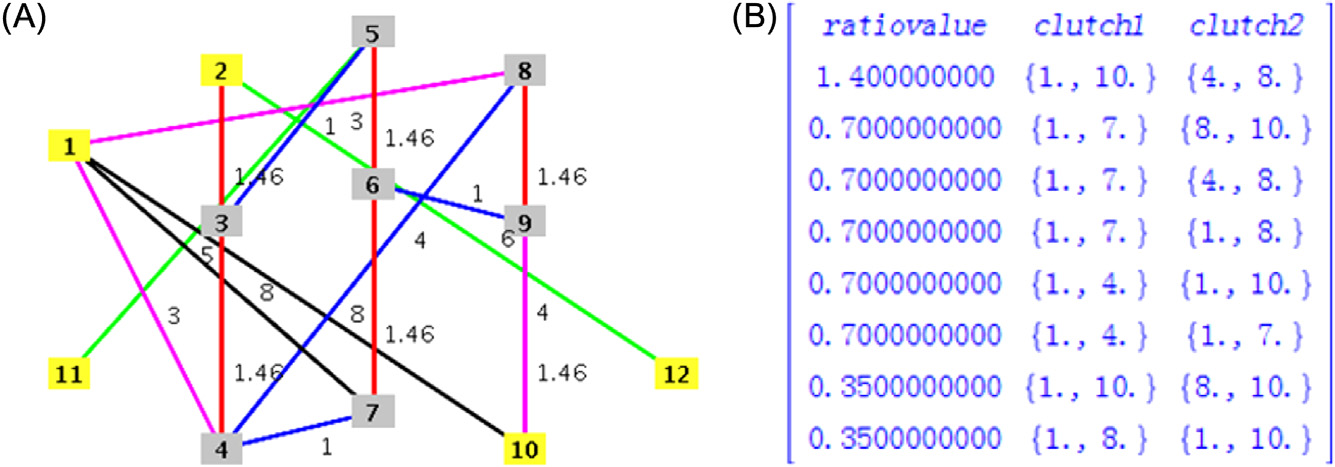
在 中,以机电复合传动机构为例,传动系统在固定边{[3,5],[4,7],[4,8],[6,9]}内的初始构型,以及初始机械点通过控制两台电机来实现。由于新的机械点位于0.35至0.7之间,新的工作模式基于两自由度基本工作模式,且新模式基于机械点0.7。当初始机械点值为0.7时,对应的控制连接状态为{[4,8],[1,7]},该机械点要求相邻工作模式对应的值为0.7,即满足模型的收敛条件1。同时,工作状态必须与电机工作需求模式的初始状态一致,即与某电机工作状态在该模式下开始工作时的工作状态一致。
通过分析 中的综合离合器序列可以发现,若实施机械点为0.35和0.7的差动变速模型有两种形式:一种是{[1,7],[8,10]}和 {[1,10],[8,10]}的组合,另一种是{[1,7],[1,8]}和{[1,10],[1,8]}的组合。因为这两种连接方式均可实现
在机械点模式下,新的差速交换速度模式和基本工作模式被选中,以满足传动连接配置的要求,还需进一步分析每种工作模式下电机的工作情况。
-
各模式下电机工况的研究
根据对传动机构转速的分析可知,两个电机在不同工作模式下的工况不同。当传动机构工作在力矩模式和速度模式时,可根据构件速度分析得到电机转速与速比之间的关系。
在多模式传动机构中,两个电机的速度应连续变化,其中电机速度的转折点即为两种模式之间的切换点。通过控制控制元件的不同连接方式来实现模式切换。在不同的工作模式下,电机的工作状态在发电和两种工况之间切换。根据对 中两种不同工作模式速度变化的分析可知,电机速度随速比线性变化。为了实现两种模式的模式切换,相邻模式下电机的速度需要满足一定条件。
4.3.5 优化算法
根据给定的设计要求,从自由度数量、特征参数的角度选择合理的结构参数、优化目标函数和约束条件行星齿轮系、电机参数以及制动器和离合器参数的数量。其应用旨在使方案更加紧凑且便于操作,其中每个元件均可被充分利用。
-
行星齿轮系特征参数的分析
在性能优良的行星传动机构中,若全部或部分具有相同的行星特性参数,则可减少零件的种类数量,加工制造工艺简便,降低成本。因此,在设计用于实现传动系统产品的行星传动机构时,应尽可能使行星排的特征参数K值保持一致。故在本章的研究中,将第一行星排的特征参数K1作为自变量,其他行星排的特征参数与K1成比例。
$$
[k_1, k_2, k_3, …, k_p] = k_1[1, x_2, x_3, …, x_p] \quad (4.6)
$$
其中,k1, k2,…,kp为第二行星排到第一行星排的行星齿轮特征参数的K值,x2, x3,…,xp为第二行星排与第一行星排特征参数的比值r,分别为x2, x3,和xp。xp的取值范围为[0.67 1.5]。当太阳轮齿数、行星轮参数较小时,齿圈齿数较多,即行星排的径向尺寸增大。行星齿轮特征参数的K值不同,太阳轮、行星轮与齿圈的尺寸比例也不同,在确定K值时,通常不希望取其边界值。对于内外啮合单星排机构,K值通常在1.8 3.5范围内取值。 -
离合器和制动器转速转矩分析
在多模式机电混合传动机构的配置中,通过控制离合器和制动器的不同结合状态来实现模式切换。根据对传动机构整体性能的分析,输入扭矩和输出扭矩取决于传动比。然而,主要功能是控制不同部件的离合器耦合状态,以及扭矩
传动方案中的需求在不同取值下各不相同。因此,需求与扭矩和离合器的方案密切相关。
传动机构中的离合器和制动器所传递的扭矩不能过大;否则,内部摩擦片的数量会增加,或摩擦片的直径变大。如果摩擦片数量过多,将导致以下问题:首先,分离离合器或制动耦合器不易分离,从而降低传动效率;其次,增加摩擦片的数量和尺寸会使离合器和制动器的重量、体积增大,在旋转过程中使其惯性增大,动载荷增加。
4.3.6 电机参数分析
电机参数分析中最重要的参数是电机功率。在不同模式下的机械和电气复合传动机构中,两个电机分别完成发电机和电机的功能;在电池供电情况下,电机功率为主分流电机功率。因此,电机功率与发动机、输出以及行星齿轮的特征参数密切相关。
在分析中,假设传动机构中没有电池组。根据离合器序列综合,发动机输出和两个电机的速度在不同模式下可表示为:
$$
\begin{bmatrix}
n_A \
n_B
\end{bmatrix}
= M_s
\begin{bmatrix}
n_e \
n_o
\end{bmatrix}
\quad (4.7)
$$
其中,Ms是机电复合行星传动机构三种模式的旋转速度关系矩阵,如表4.3所示。
双电机耦合系统在三种模式下的分析与发动机扭矩和输出扭矩的分析类似。输出扭矩可以表示为:
$$
\begin{bmatrix}
T_A \
T_B
\end{bmatrix}
= M_T
\begin{bmatrix}
T_i \
T_o
\end{bmatrix}
\quad (4.8)
$$
其中,对于扭矩关系矩阵中的机电混合传动机构,有三种工作模式的扭矩关系矩阵。
4.3.7 计算机综合程序
切换模型的筛选流程图和构型生成的综合算法分别如 和 所示。
4.3.8 结果
双模式和三模式传动方案分别如 和 所示。
4.4 并联式混合动力电动汽车传动系统拓扑设计
由于排放更低且能效更高,全球领先的汽车制造商已开发出电动和混合动力电动汽车。尽管目前纯电动汽车是汽车行业最终追求的目标,但现阶段仅适用于小众市场。汽车制造商已研发出多种混合动力架构,包括串联式、并联式以及复杂的串并联类型。由于自动机械变速器(AMT)不仅是效率最高的自动变速器,而且也是成本最低的自动变速器,因此通常由电动机和AMT组成的并联架构目前在混合动力汽车中应用最为广泛。
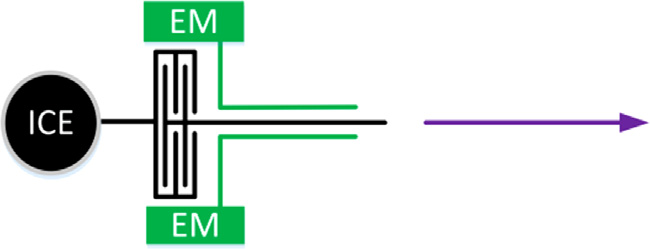
通常,根据电机布局,并联式混合动力汽车可分为三类。第一种类型()中,电动机位于前方传统自动机械变速器的。尽管电动机可以使用传动系统中的所有齿轮,但在换挡过程中没有扭矩支持。第二种类型()中,电动机位于传统自动机械变速器之后。这种类型能够实现换挡时的扭矩支持,但电动机仅能使用一个固定的齿轮。最后一种类型()中,电动机与自动机械变速器的结合可以在与标准自动机械变速器相同的机械复杂度下,为电动机提供多个传动比,并在换挡过程中提供扭矩支持。因此,本章重点讨论最后一种类型的并联式混合动力汽车,通常称为动力换挡变速器(PST)。
PST的结构类似于两个传动系统耦合在一起,比传统的自动机械变速器更为复杂。在不增加标准自动机械变速器的机械复杂性(齿轮副数量、同步器和轴系)的情况下,PST可以提供多个内燃机档位。
通过提高机构组件的利用率,可实现多个电机齿轮。因此,传统的自动机械变速器设计方法不适用于动力换挡变速器方案的设计。对于像动力换挡变速器这样的定轴齿轮传动,不同的档位意味着根据同步器状态,功率流从输入端到输出端经过不同的齿轮副和轴。为了实现动力换挡功能,换挡序列必须遵循一定的换挡逻辑。基于这些原因,将变速器方案的具体结构抽象为顶点,边则基于方案的自由度来研究换挡序列。然后,从基本构型定义的转速自由度和转矩自由度出发,通过研究基本构型的可变构造拓扑,得到衍生功能的拓扑综合方法。最后,根据综合结果布置同步器并设计传动比()。最终,提出了一个并联式混合动力汽车用动力换挡变速器的示例方案及其换挡序列。
4.4.1 换挡序列研究
传动系统的自由度(DOF)定义为用于确定运行条件的独立且可任意设定的参数或状态的数量。由于存在包括内燃机和电动机在内的两个动力源,PST包含三个自由度,它们分别与内燃机、电动机和输出轴相连,以实现动力换挡。
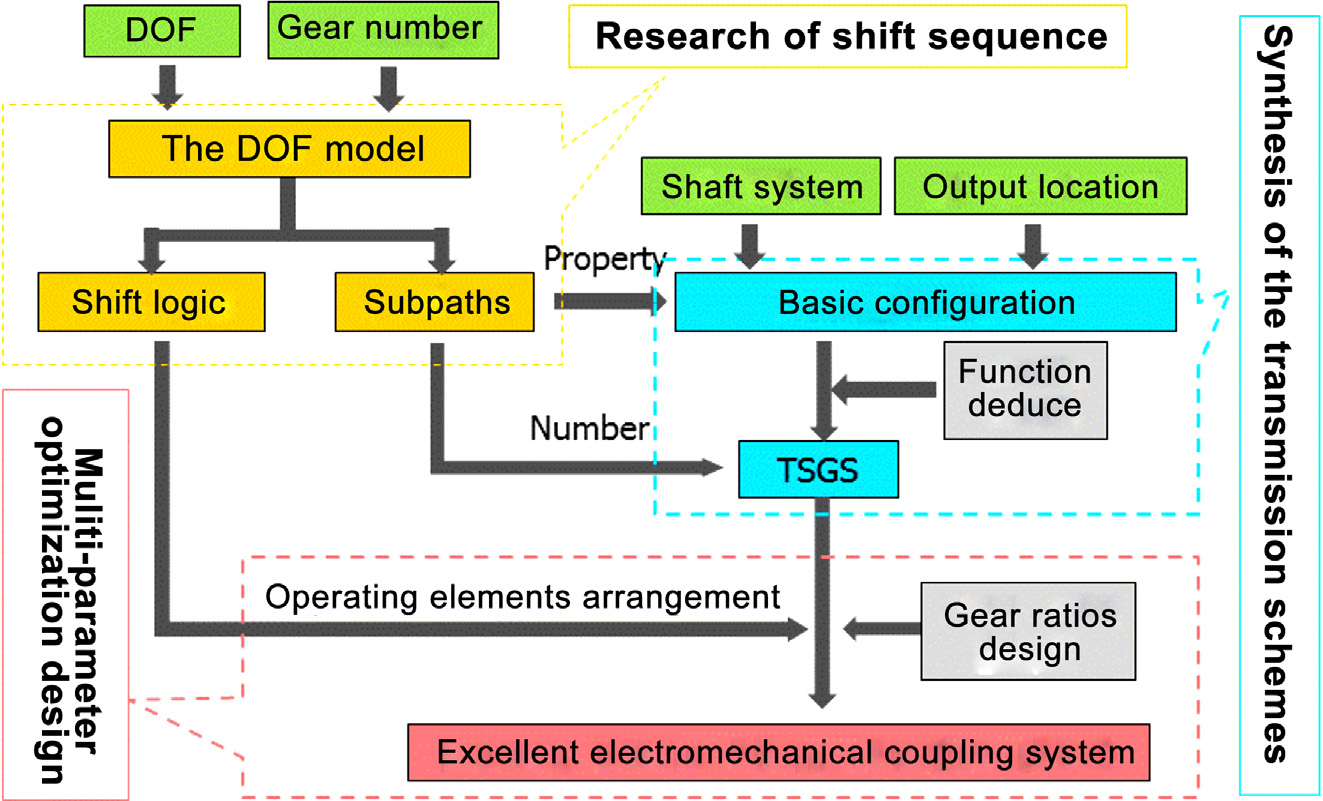
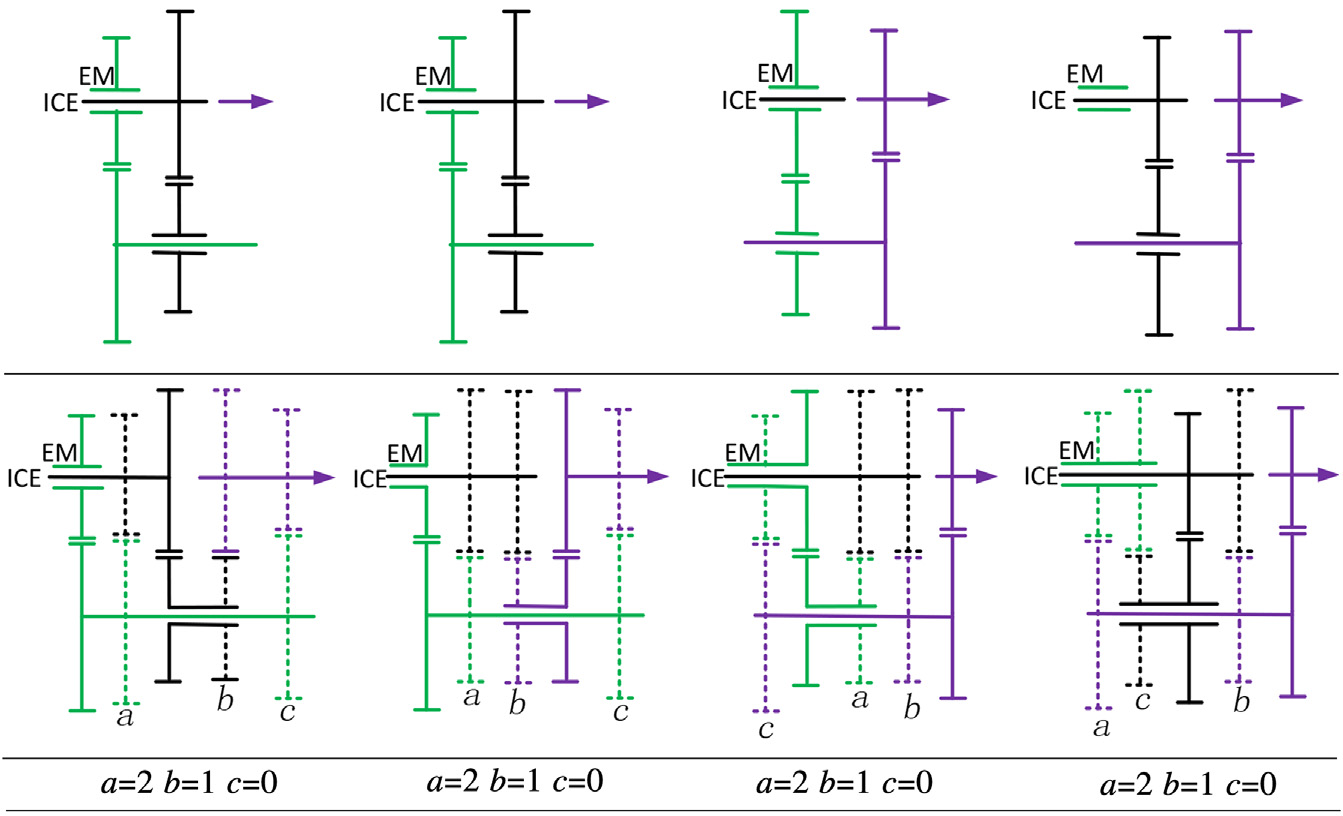
变量连接(VC)定义为齿轮副中一个齿轮永久连接到轴或空心轴,另一个为惰轮,且同步器的状态决定该惰轮是否与轴连接。当同步器不工作时,属于自由度的所有构件(除虚拟构件外)由顶点表示,而虚拟构件由顶点之间的边表示。因此,所有具有三个自由度的PST(如 所示)均可由 所示的自由度模型表示。
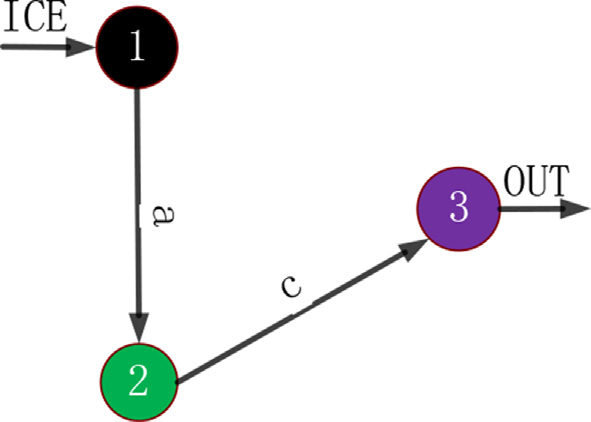
顶点F1,F2,和F3分别表示连接到内燃机的自由度、连接到电动机的自由度以及连接到输出轴的自由度。边a、b和c分别表示F1与F2,、F1与F3, 、F2与F3,之间的虚拟构件。两个自由度之间边的权重等于它们之间虚拟构件的数量。例如,在 中,F2与F3之间包含c1和c2两个虚拟构件,因此边c的权重为2。
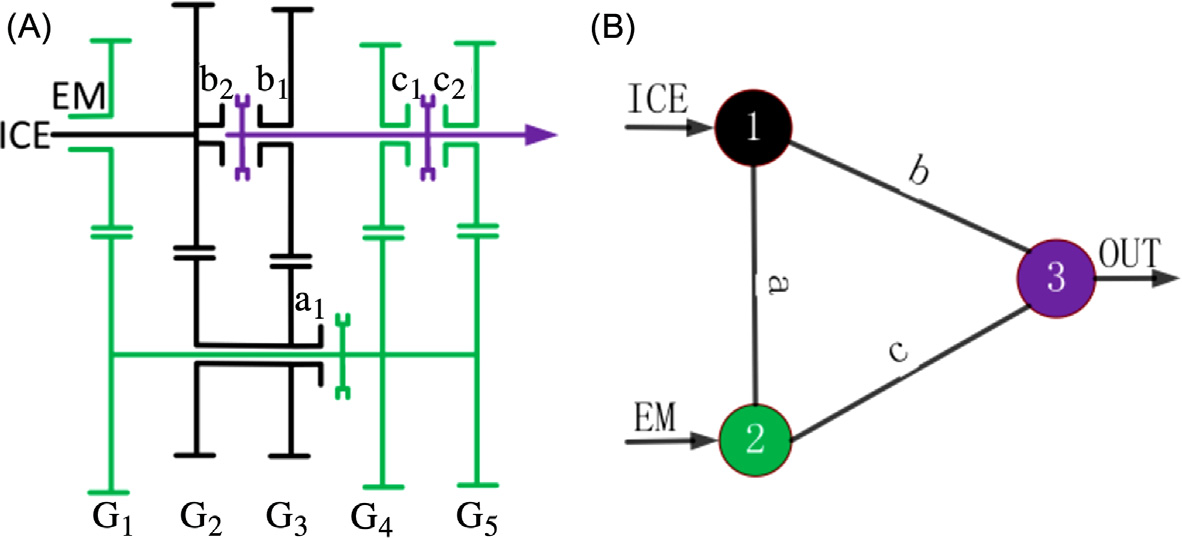
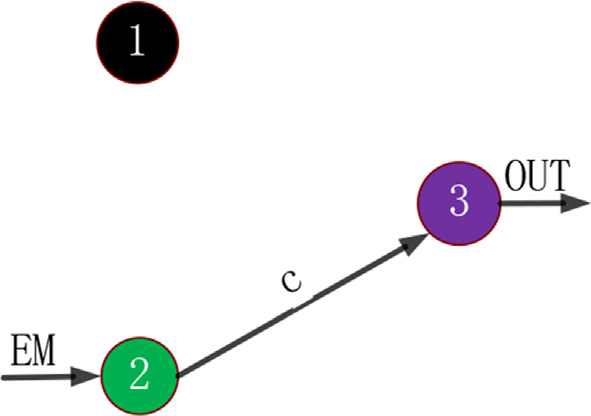
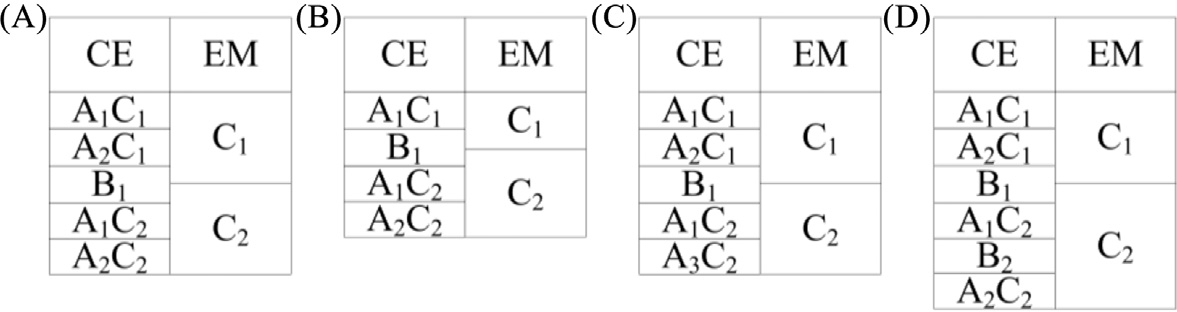
PST中有两种齿轮:内燃机齿轮和电机齿轮。自由度模型中的功率流如 所示。当 中的同步器a1和c1工作时,形成一个称为 A1C1 的内燃机档位。内燃机的功率最终通过齿轮副G2,中间轴的套筒、同步器a1,齿轮副G4,以及同步器c1传递到输出轴,如 所示。在 所示的自由度模型中,可将其简化为F1 a1 F2 c1,这是分析内燃机和电机齿轮的功率流及虚拟构件的一种简便方法。
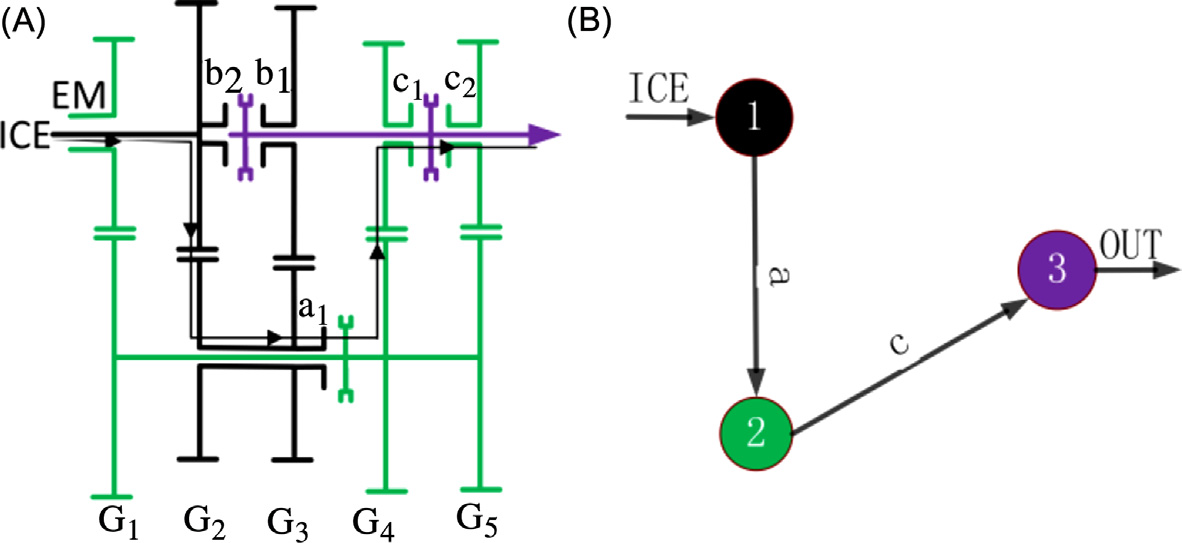
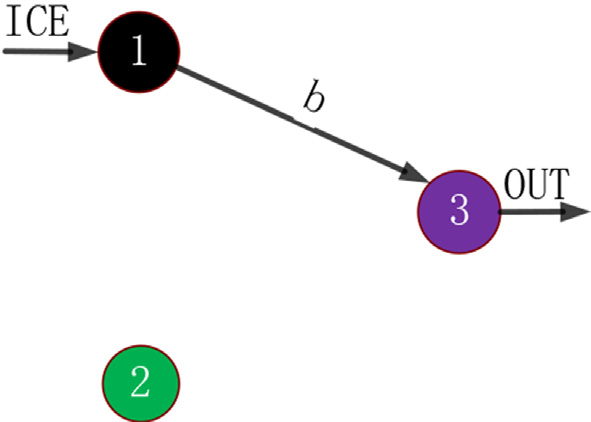
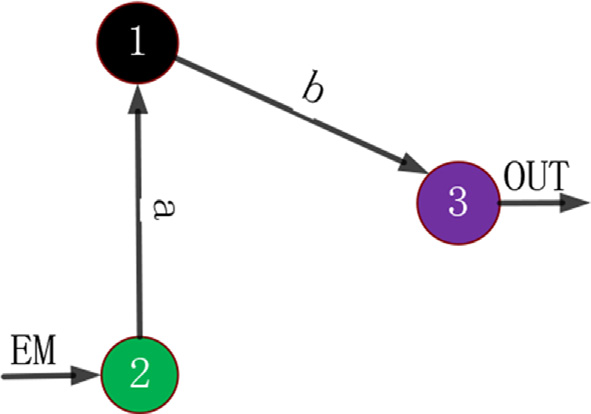
PST具有三个自由度,其上有两种功率流,即内燃机齿轮和电动机齿轮。其中一种是输入自由度(F1或F2)直接连接到输出自由度(F3),而不经过中间自由度(F2或F1)。例如内燃机档位B1,的功率流为F1 b1 F3, 且F2不参与。另一种情况是输入自由度(F1或F2)通过中间自由度(F2或F1)连接到输出自由度(F3)。例如内燃机齿轮A1C1, ,其功率流为F1 a1 F2 c1 F3。这些功率流形式如表4.2所示。内燃机齿轮 AC或电动机齿轮AB被定义为双动力齿轮,因为两个动力源的自由度都参与了该档位的形成。当内燃机齿轮为AC或电动机齿轮为AB时,电动机或内燃机的档位必须分别为C或B。一旦共用的变矩器断开,内燃机齿轮和电动机齿轮都将消失。例如,当内燃机齿轮处于A1C1,时,功率流为F1 a1 F2 c1 F3, ,所有动力源的自由度均参与,此时电动机齿轮必须为C1。一旦共用的变矩器C1断开,内燃机齿轮A1C1和电动机齿轮C1都将消失。为了提供扭矩支持,在内燃机齿轮换挡过程中,电动机齿轮必须保持原有档位不变;同样,在电动机齿轮换挡过程中,内燃机齿轮也必须保持原有档位不变。因此在双动力换挡过程中,共用的变矩器不能断开。当一个动力源的齿轮处于双动力齿轮状态时,另一动力源的齿轮无法在有扭矩支持的情况下进行换挡。因此当内燃机(电动机)进行齿轮换挡时,电动机(内燃机)齿轮必须处于C(B)档。
本章中,我们研究的PST具有以下特点:1. 每个电动机档位对应三个或四个内燃机档位,因为电动机的工作范围通常比内燃机长三到四倍。2. 速比级差从低档到高档逐渐减小,以获得车辆在低速时良好的加速性能和高速时优异的燃油经济性。
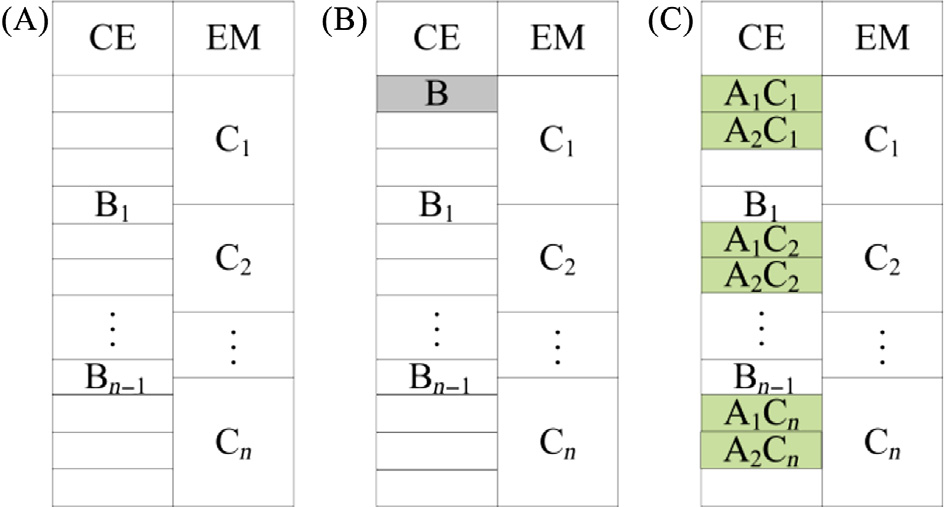
当电动机档位处于双动力档位时,电动机档位在换挡期间无法提供扭矩,并且每个电动机档位连接两个或三个内燃机齿轮。电动机齿轮必须始终位于离合器C。在电动机齿轮换挡期间,内燃机齿轮必须位于制动器B。电动机齿轮和内燃机齿轮的换挡序列如 所示。至少有n个电动机档位C,包括C 1 ,C 2 ,⋯⋯、Cn,以及n2个内燃机档位B,包括B 1 , B 2 ,⋯⋯、Bn 2 1。因为
| DOF | 功率流 | Gear参与 | 自由度模型 |
|---|---|---|---|
| F1 制动器 F3 |
B
AC C AB |
F1 F3
F1 F2 F3 F2 F3 F1 F2 F3 | F1 a F2 c F3 |
| F2 离合器 C F3 | F2 a F1 b F3 |
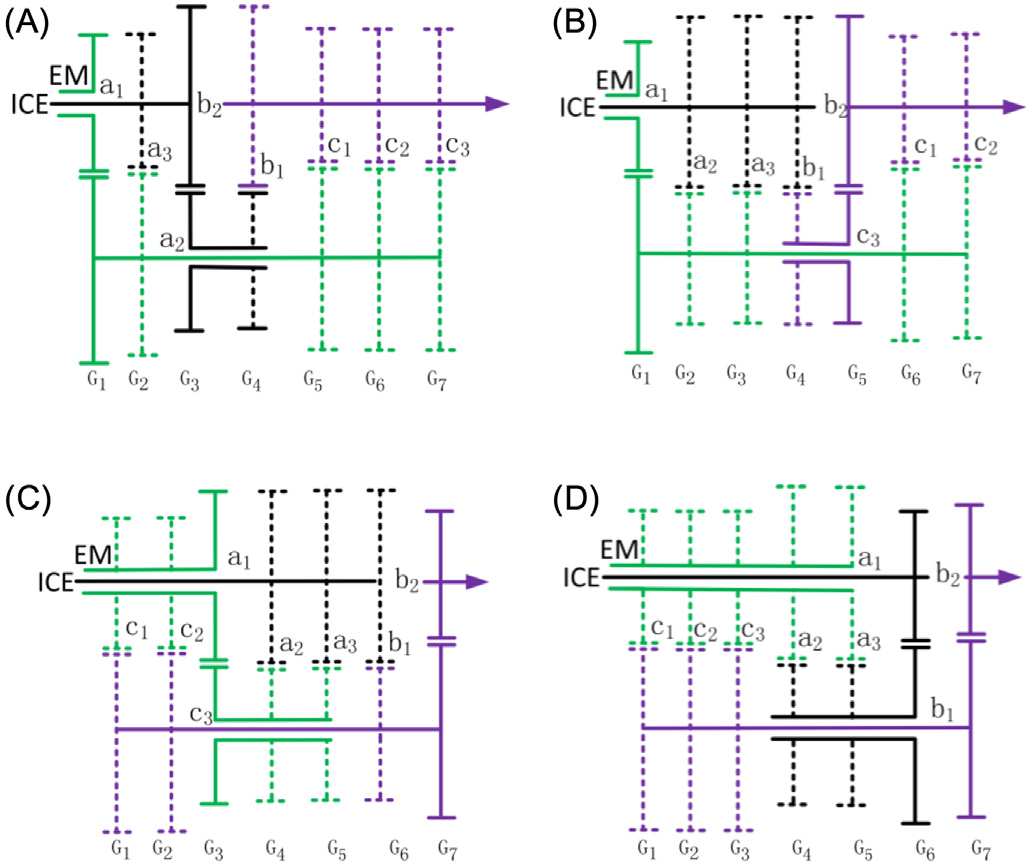
每个电动机档位最多可对应四个内燃机齿轮,其他内燃机齿轮应添加到换挡序列的空缺位置。这些空缺位置可以用内燃机档位B、交流电或留空填充。当添加一个变矩器b时,将形成一个新的内燃机档位B,并可放置在任意空缺位置,如 所示。当添加一个变矩器a时,将形成一个新的内燃机齿轮ACi,其数量对应于离合器C的电动机档位数量i,如 所示。
由于电机齿轮必须为离合器C,因此电机齿轮的数量为:
$$
n_{EM_gear} = n_c \quad (4.9)
$$
其中nc是变矩器c的数量。
由于在电机齿轮换挡期间内燃机齿轮必须处于制动器B档,因此变矩器b的数量不少于变矩器c的数量减一,如下所示:
$$
n_b \geq n_c - 1 \quad (4.10)
$$
其中nb是VC b的数量。
如果使用所有虚拟构件,则内燃机齿轮的数量为:
$$
n_{CE_gear_max} = n_a \times n_c + n_b \quad (4.11)
$$
其中na和nCE_g ear_max分别为VC a的数量和所有内燃机齿轮的数量。
当VC a的数量为2时,形成{n}个内燃机齿轮交流电,如图4.32C所示。由于A1C1和A2C1具有相同的变矩器c1,,A1C1与A2C1之间的速比级差等于VC a1的速比除以VC a2的速比。类似地, A1Ci与A2Ci之间的速比级差等于VC a1的速比除以VC a2的速比。所有A1Ci与A2Ci之间的速比级差都相同。当VC a的数量为大于2时,我们可以通过删除一些内燃机齿轮交流电,或添加如制动器和交流电等内燃机齿轮来获得逐步减小的速比级差。例如, 中的换挡序列包含两个变矩器 a、一个变矩器 b和两个变矩器 c。然后生成五个内燃机档位和两个电动机档位,且A1C1, A2C1与A1C2, A2C2之间的内燃机速比级差相同。从低档到高档获得逐步减小速比级差的方法有三种,分别如 、C和D所示。
4.4.2 变速器方案综合
为了减小重量和尺寸,并便于在传统车辆中布置,本章讨论的 PST具有两个特殊特性: 1.电动机、内燃机和输出轴同轴布置,如图4.4.24所示。2.存在包含轴和空心轴的双轴系统。
基本构型定义为方案派生的基础,必须包含自由度模型中每个虚拟构件至少一个。通过根据换挡序列的需求添加虚拟构件,可以获得齿轮副和轴的方案。
对于具有双轴系统的PST,如图4.4.24所示,第一轴系包括属于自由度F1 ,的内燃机输入轴、属于自由度F2 ,的电机输入轴以及属于自由度F3的输出轴。第二轴系必须位于三个自由度之内
如上所述,这意味着第二轴系中的轴和空心轴必须通过固定齿轮副与第一轴系永久连接。
有四种轴布置形式,如表4.3第一行所示,这些是3‐自由度模型中顶点的具体结构。虚拟构件在基本构型中用虚线表示。四种基本构型如表4.3第二行所示。如果同步器连接同一轴系中的轴与空心轴或轴与轴,则会形成一个附加虚拟构件。在第一轴系中,内燃机输入轴和电机输入轴可形成附加虚拟构件a,内燃机输入轴和输出轴可形成附加虚拟构件b。附加虚拟构件b是PST的直接挡。在第二轴系中,根据四种基本构型的不同布局,可能形成a、b或c,如表4.3第三行所示。
所有四种基本构型均由五对齿轮副组成,包括两个永久连接和三个虚拟构件。永久连接是指齿轮固定在轴上,用于与一个自由度内部进行关联。齿轮副的数量ng ear-p air可通过虚拟构件和永久连接的数量获得,例如:
$$
n_{gear-pair} = n_{permanent} + n_{additional} + n_a + n_b + n_c \quad (4.12)
$$
其中,npermanent为永久连接的数量,nadditional为附加虚拟构件的数量,na、nb和nc分别为虚拟构件a、b和c的数量。
4.4.3 多参数优化设计
本章考虑了同步器的形式和传动效率。当同步器布置在PST上时,应具备三种状态:右啮合、左啮合和分离。这种布置可减少同步次数和执行器数量,便于换挡过程中对同步器的控制,并减小变速箱的轴向尺寸。传动效率越高,车辆的动态性能和舒适性性能越好,功率损失越小,噪声和振动越低。
内燃机速比起着关键作用,而电动机速比也在内燃机换挡过程中提供扭矩支持,以克服扭矩中断。因此,速比设计基于内燃机速比的需求。由于所有传动比均由方案中的齿轮副构成,齿轮之间必然存在线性关系。因此,实际速比无法完全等于目标速比。此外, PST变速器的传动比设计具有矛盾性,可转化为超定非线性方程组的求解问题:
$$
R_2 = \frac{R_1}{1 + a_x} \
R_3 = \frac{R_1}{(1 + a_x)(1 + r a_x)} \
R_4 = \frac{R_1}{(1 + a_x)(1 + r a_x)(1 + r^2 a_x)} \
\vdots \
R_n = \frac{R_1}{\prod_{k=0}^{n-2} (1 + r^k a_x)} \quad (4.13)
$$
根据换挡序列和车辆需求确定直接挡和一挡速比的数量。为了提高驾驶性能,其余传动比按速比级差构成几何序列进行计算。
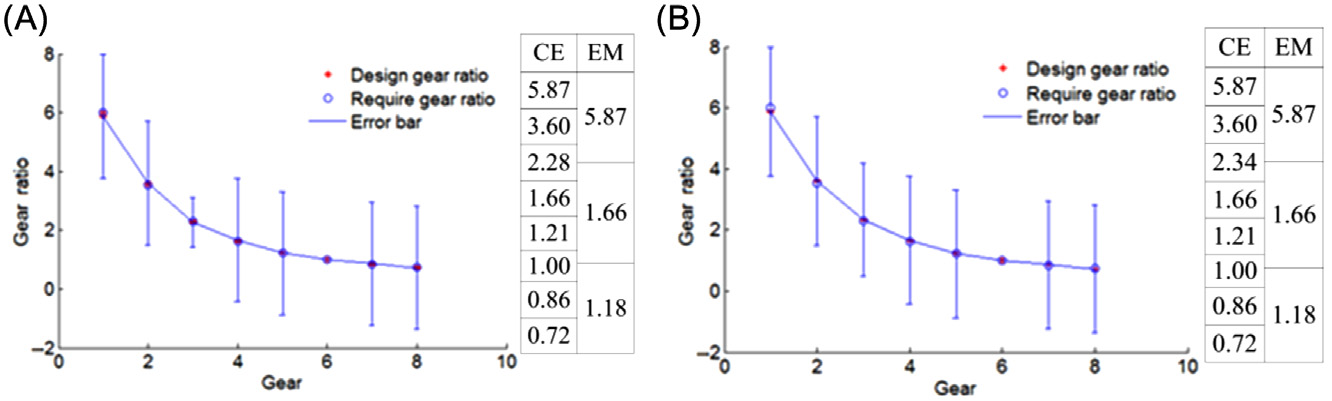
PST的内燃机速比如公式(4.13)所示,其中a x等于传动比的要求一档传动比与二档传动比之间的速比。根据给定的一档传动比ax和直接挡的位置求解比值r。然后得到PST上内燃机所需的传动比。
通过将各传动比的无穷范数和欧几里得范数的最小化作为优化目标,超定非线性方程组的求解可以转化为多个变量的优化问题:
$$
\min(\max|f(i) - R_i|/R_i) \quad (4.14)
$$
$$
\min \left( \sum \left( \frac{f(i) - R_i}{R_i} \right)^2 \right)^{0.5} \quad (4.15)
$$
其中f(i)和Ri分别表示设计传动比和所需传动比。如果无穷范数小于6%,则实际传动比是可接受的。
4.4.4 设计方法示例
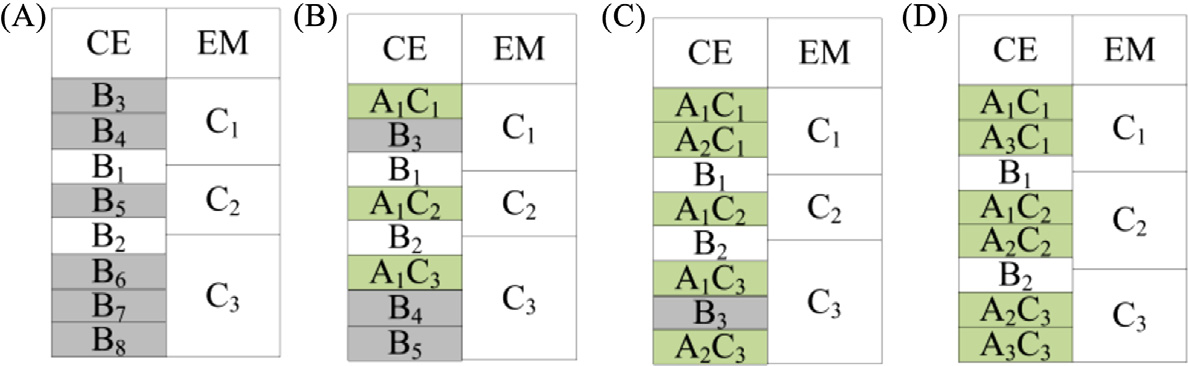
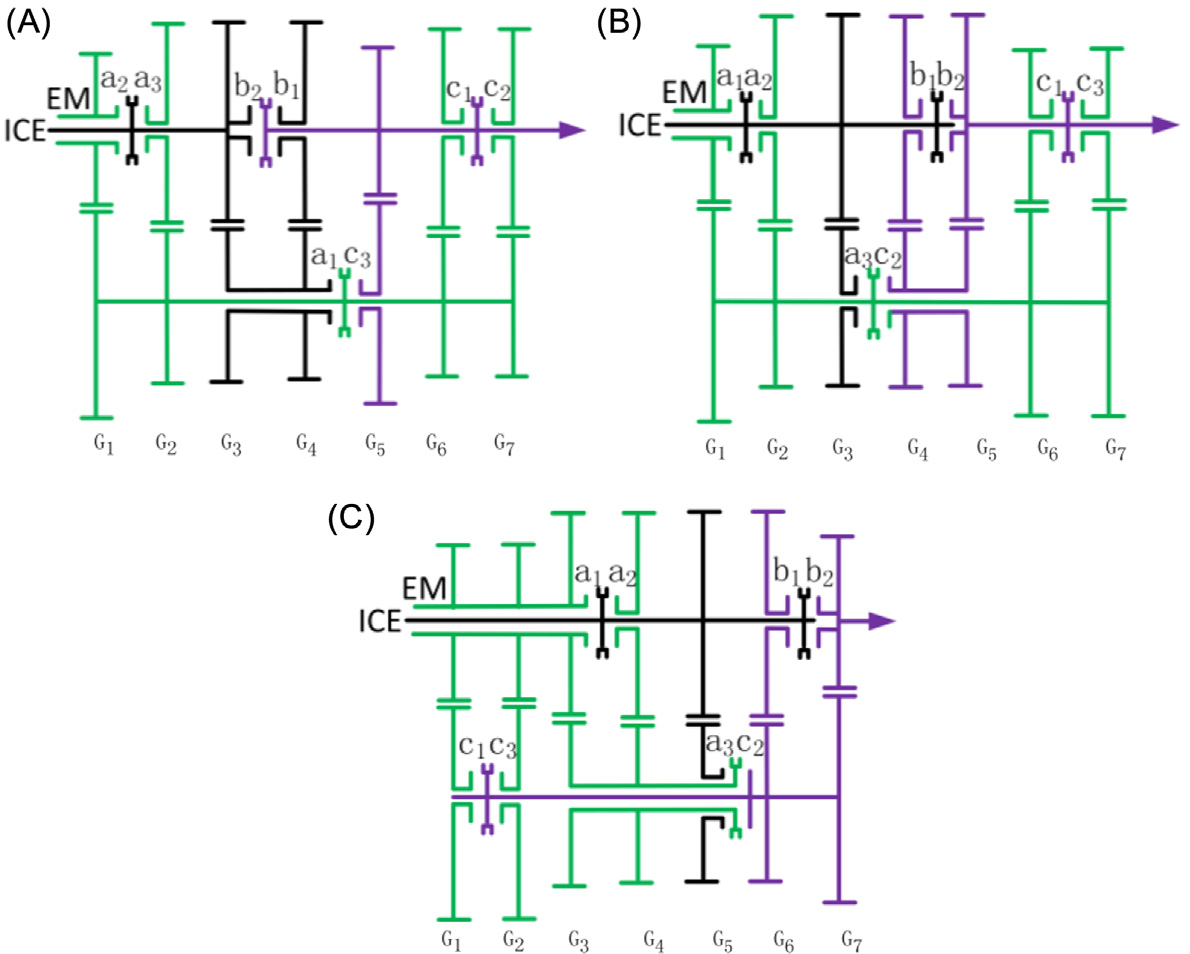
以包含8个内燃机齿轮和3个电动机齿轮的PST为例进行设计。如 所示,共有四种类型的方案。通过比较虚拟构件的总数可以看出,在实现相同齿轮数量的前提下,第三和第四种换挡序列所需的虚拟构件较少。我们选择第四种换挡序列323作为研究齿轮 轴配置综合与优化设计的示例。
VCs的数量a、b和c分别为3、2和3。因此,可根据这些VCs推导出基本构型,结果如 所示。在方案323‐1、323‐2和323‐3中




















 35
35

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








