PLVA：轻量隐私保护V2I认证

PLVA：隐私保护且轻量的车对基础设施（V2I）认证协议

摘要

车载自组织网络（VANETs）通过减少交通拥堵和避免事故，显著提高了驾驶的效率与安全性，其中必要的安全目标通过密码学方法得以保障。在实际中，计算效率对于在车载自组织网络中实现协议至关重要。当一辆高速行驶的车辆进入路侧单元（RSU）的覆盖范围时，认证过程的计算开销不仅影响通信体验，还可能降低驾驶安全性。一种可行的解决方案是在证书颁发机构（CA）的帮助下，车辆与路侧单元提前共享消息，然而这可能导致证书颁发机构推断出车辆应受保护的路线规划。本文提出了一种隐私保护轻量级车对基础设施认证（PLVA）协议。具体而言，在初始阶段，利用摩尔曲线技术将一个区域内的所有路侧单元（RSUs）转换为一个向量；然后，在车辆开始行程之前，该车辆使用BGN同态加密推导出其规划路线上的路侧单元信息，而在此过程中，尽管证书颁发机构（CA）提供了协助，却无法获知任何关于路线规划的信息。基于所推导的路侧单元信息，车辆与其路线上的每个路侧单元之间实现了快速认证。此外，性能评估表明，我们的PLVA在实际的车载自组织网络环境中具有较高的计算效率。

关键词 —车载自组织网络、BGN同态加密、摩尔曲线、快速认证、隐私。

一、引言

在未来，车辆可能成为全球第三大移动终端。如何提高交通效率并减少交通事故已成为备受关注的问题。随着人工智能技术的不断发展，自动驾驶技术已应用于车辆，但仍会发生严重的交通事故[1]。因此，为了保障自动驾驶的安全，有必要将车辆状态、天气状况、道路情况等实时信息传递给其他车辆及周边设备。车载自组织网络（VANET）将逐步发展为智能交通系统（ITS）[2],[3]。

在车载自组织网络（VANET）中，车辆借助电子标签与其他车辆（车对车，V2V）或路侧单元（RSU）（车对基础设施，V2I）进行通信。安装在车辆上的车载单元（OBU）。如今，已有多种算法被提出以确保车对车（V2V）[4]–[6]通信的安全性和可靠性。通常情况下，路侧单元（RSU）连接车载单元（OBU）、证书颁发机构（CA）或云服务器，然后允许车载单元（OBU）接入互联网或证书颁发机构（CA）。由于专用短程通信（DSRC）的最大通信距离为1000m[7]，消息传输容易受到攻击者窃取。因此，车对基础设施（V2I）通信应具备高安全性和高效性[8]。

基于密码学的认证通常分为非对称和对称两类，其中大多数是基于非对称密码系统[9],[10]，但其在车载自组织网络（VANET）中效率较低[11],[12]。尽管对称密码系统效率较高，但隐私和安全性无法完美实现。最近，Liu et al.提出了LVAP方案[13]，其中证书颁发机构（CA）建立一个包含车辆和路侧单元（RSUs）的组，通过共享密钥快速执行认证。然而，车辆的路线规划容易被CA获取。基于签名的认证方案旨在解决这一弱点[14]–[16]，但需要公钥基础设施（PKI）[15]等实体来生成和分发公钥/私钥，并且通信开销相对较高。EAAP方案基于签名认证[13]。当车辆进入不同的RSU区域或发送消息时，需要计算不同的证书供RSU验证。当RSU验证车辆的消息时，也需要大量计算资源来验证证书的有效性。批量验证不仅能有效解决密钥管理和通信开销问题，还能实现对大量消息的快速认证[17],[18]。在曾氏方案[17]中，无论验证多少条消息，仅需执行两次双线性对运算和一次点乘运算。然而，当攻击者发送恶意篡改消息时，曾氏方案的效率会受到极大影响。

本文提出了一种基于BGN同态加密[19],[20]的隐私保护轻量级车对基础设施认证（PLVA）协议，车辆在开始行程前获取其路径上路侧单元（RSUs）的信息。一方面，在进入路侧单元覆盖范围时可实现快速认证；另一方面，证书颁发机构无法得知车辆推导了哪些路侧单元的信息，从而保护路线隐私。

其余部分组织如下：第2节介绍预备知识，第3节提出系统模型和设计目标。我们的PLVA在第4节中提出，性能分析和结论分别在第5节和第6节。

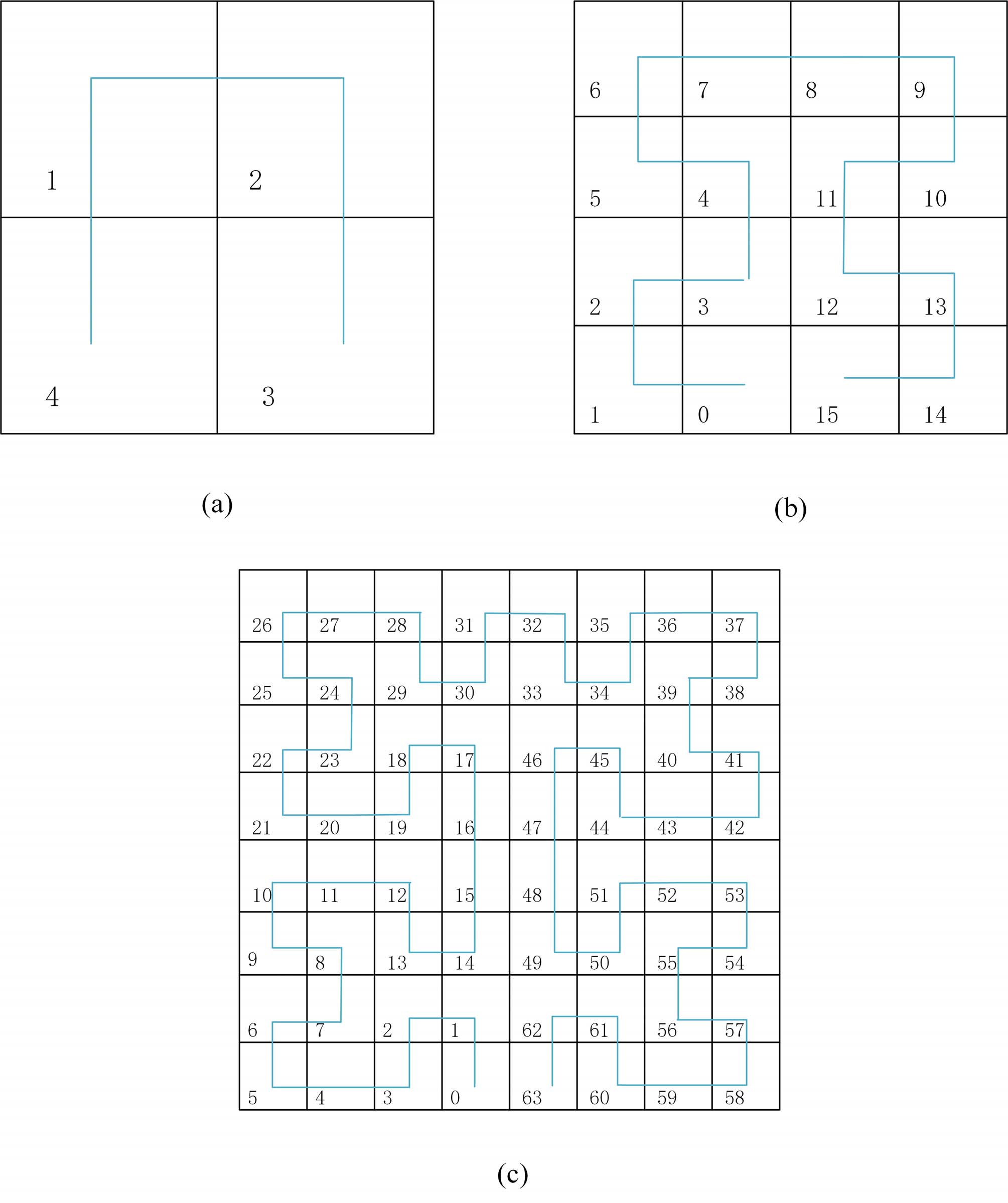阶数为N= 1的摩尔曲线，(b) 阶数为N= 2的摩尔曲线，(c) 阶数为N= 3的摩尔曲线)

II. 预备知识

A. Moore曲线

当地图表示为二维矩阵时，需要大量的计算资源。如果将地图从二维矩阵转换为一维向量，则计算复杂度大大降低。由于摩尔曲线是一条遍历 2N × 2N单位正方形中所有点以生成[21]空间完整曲线的连续且不自交的曲线，因此被广泛应用[22]–[24]。图1展示了不同阶数N的摩尔曲线。

B. BGN

BGN 是一种同态加密方案，可执行加法同态和一次乘法同态操作。

密钥生成 ：使用安全参数τ生成复合双线性配对(G, GT, e, g0, N)，其中G, GT 是两个阶为N == pq的群，映射G × G = GT。h == gq0 是阶为p的G的子群的生成元。公钥 PK=(N, G, GT, N, g0, h) 被公开，同时私钥 SK= q 被保密。

• 加密 ：为了加密消息 m，计算密文 C=E(m, r)=gm0 hr，其中 r ∈Z N是一个随机数。
• 解密 ：利用 C= gm0 hr和 SK= q，当 m位于非密码学大空间的集合中时，可通过波拉德λ算法猜测满足 Cq = ( 0)=( 0) [25]g m h r qgq m的 m 来获得明文消息。

BGN方案的同态性质包括：

• 加法 : C= C1C2 · hr= gm10 hr1 · gm20 hr2 ·hr= gm1+m20 hr1+r2+r
• 乘法 ：g1= e(g0, g0), h1= e(g0, h)，g1,h1 的阶分别为 n,q。

C= e(C1, C2) h r 1= e(gm1 0 hr1, gm2 0 hr2) hr 1 = gm1m2 1 hm1r2+m2r1+qr1r2+r 1 (1)

III. 模型

A. 系统模型

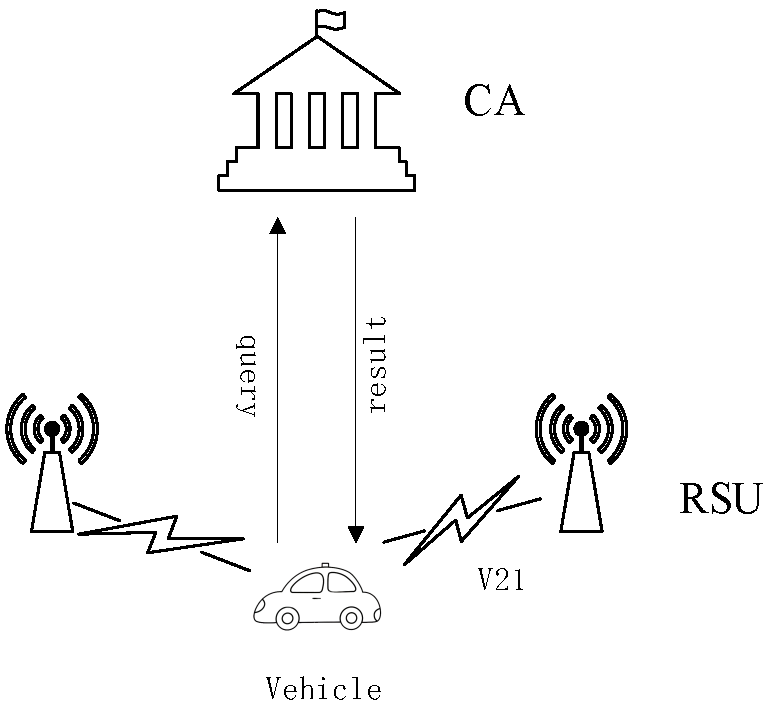
一个简单的模型包括证书颁发机构、路侧单元和车辆，如图2所示。

• CA ：假设证书颁发机构为半可信的，即证书颁发机构可能会尝试利用合法接收到的消息推导出有价值的信息。此外，作为车载自组织网络的管理者，证书颁发机构存储路侧单元信息，并帮助路侧单元对车辆进行认证。
• RSU ：路侧单元接收并转发其覆盖范围内的车辆发送的消息。
• 车辆 ：配备OBU和TPD模块的车辆与RSU和证书颁发机构交换消息，TPD存储私有信息并执行安全计算。

B. 设计目标

必要的设计目标包括:

• 消息完整性 ：当消息在开放信道上传输过程中被篡改时，接收方应能检测到该情况。
• 消息机密性 ：攻击者无法从窃听的消息中获取任何有效信息。
• 身份匿名性 ：即使所有路侧单元（RSUs）都被攻破，在路侧单元与证书颁发机构无法共谋的假设下，也无法推断出车辆的真实身份。
• 路径规划隐私 ：证书颁发机构帮助车辆获取其路径上路侧单元的信息，但无法得知车辆具体推导出了哪些路侧单元的信息。

IV. PLVA方案

PLVA方案包括四个阶段：初始阶段、注册阶段、查询阶段、认证阶段。在初始阶段，CA生成并发布安全参数和路侧单元（RSUs）的信息。在注册阶段，车辆与证书颁发机构共享必要的信息。在查询阶段，车辆向证书颁发机构查询并推导出其路径上路侧单元（RSUs）的信息，同时证书颁发机构无法得知车辆获取了哪些路侧单元的信息。随后，车辆与路侧单元之间实现快速认证。

A. 初始阶段

1) 证书颁发机构生成一个公钥/私钥对（公钥 PKCA, 私钥 SKCA），并向路侧单元 RSUi颁发 NORSUi。
2) 路侧单元 RSUi选择其对称加密密钥 KRSUi ∈Z p作为认证密钥，然后将 KRSUi发送给证书颁发机构。K RSUi会定期更新，例如每天更新一次。
3) 证书颁发机构使用摩尔曲线处理实际地图，使得实际地图中包含 n个单元格，每个单元格拥有自己的标签和一个路侧单元 RSUi，如图1所示。证书颁发机构设置信息向量（H信息）：{m1:(1 ∥ ∥N ORSU1 ∥ m2:(2 ∥ ∥N ORSU2 ∥ ∥N ORSU i ∥ ∥ K RSUi‖i n foi), …, mn:(n ∥∥N ORSUn ∥ 其中 i n foi是路侧单元 RSUi的道路信息，KRSUi是路侧单元 RSUi的认证密钥，N ORSU i对应每个单元格中的路侧单元 RSUi。
4) 证书颁发机构使用摩尔曲线发布实际地图以及{GCA, qCA, g, 公钥 PKCA}给其他实体，并私下保存SKCA,KRSUi和H信息。

B. 注册阶段

1) 车辆的可信处理设备选择参数 τ生成复合双线性参数 (G, GT, e, g0, N)，然后发布公钥 PKv=(N, G, GT, N, g0,h)，并私下保存私钥 SKv= q。
2) TPD 选择随机数 rnn，并将 rnn和 IDv （真实车辆身份）发送给证书颁发机构。
3) 证书颁发机构验证车辆的身份，并为车辆的 IDv生成假名 PIDv。
4) 证书颁发机构生成一条哈希链 {rn−1=H (rnn) ,···, rni=H (rni+1) ,···, rn0=H (rn1)}，其中 H (·)，该哈希链从 rn0到 rnn使用。
5) 证书颁发机构将 PIDv、哈希链 {rn0,···, rnn}以及 PWD 写入每辆车辆，同时存储这些信息，其中 PWD 由证书颁发机构随机选择。

C. 查询阶段

1) 每个车辆的可信处理设备使用Dijkstra算法[26]在实际地图上预测其路径。若经过某个单元格，则将其设为1，否则设为0。然后可信处理设备使用Moore曲线将地图转换为序列L。例如，cell0,cell1,和cell2被设为1，而 cell3表示为0，则路径序列L={1, 1, 1, 0}。

TPD 使用 BGN 对 L 进行加密。为了更高效地执行，TPD 预先计算每个单元格的两个加密值 C 1 i = g 1 0 h r i 和 C 0 i = g 0 0 h r i，分别表示预测路径将经过的单元格和不经过的单元格。

通过L={1, 1, 1, 0}，被加密的L表示为EL={C1 0, C1 1, C1 2, C0 3}。

2) 如果EL直接发送给证书颁发机构，车辆的轨迹很容易被证书颁发机构通过其之前的查询推断出来。TPD选择一个随机数 ∂，并将EL旋转 ∂，因此在没有∂[21]的情况下，证书颁发机构无法获得关于车辆轨迹的任何信息。TPD需要计算一个循环移位矩阵P= Pi,j,(i,j= 1,2,3 …, n)，其中

Pi,j={1 j=i+(n − ∂) mod n 0 otherwise (2)

然后，矩阵 P=Pi,j,(i,j= 1,2,3 …, n)被加密。

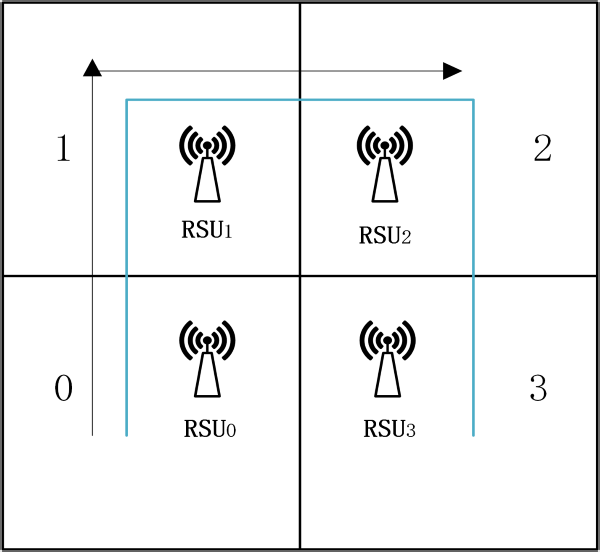
具体而言，TPD 对第一行进行加密，其余行通过对第一行进行置换生成。因此，可以预先计算出一个加密矩阵 EP。在图3中，假设 ∂= 2，以及循环移位矩阵

P=
⎛⎜⎜⎝ 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 ⎞⎟⎟⎠ (3)

接着，TPD对第一行进行加密，然后移动加密后的第一行以得到其他行，如公式(5)所示。

EP →
⎛⎜⎜⎝ g 0 0h r0 g 0 0h r1 g 1 0h r2 g 0 0h r3 0 0 0 1 1 0 0 0 0 1 0 0 ⎞⎟⎟⎠ →
⎛⎜⎜⎝ g 0 0 hr 0 g 0 0 hr 1 g 1 0 hr 2 g 0 0 h r 3 3 0 0 hr 3 g 0 0 hr 0 g 0 0 h r 1 1 g 1 0 hr 2 1 0 0 0 0 1 0 0 ⎞⎟⎟⎠ (4)

然后，得到加密矩阵 EP。

EP=
⎛⎜⎜⎜⎜⎝ g 0 0 hr 0 g 0 0 hr 1 g 1 0 hr 2 g 0 0 hr 3 g 0 0 h r 3 g 0 0 h r 0 g 0 0 h r 1 g 1 0 h r 2 g 1 0 h r 2 g 0 0 h r 3 g 0 0 h r 0 g 0 0 h r 1 g 0 0 h r 1 g 1 0 h r 2 g 0 0 h r 3 g 0 0 h r 0 ⎞⎟⎟⎟⎟⎠ (5)

3) TPD 计算临时伪名 SPID v=H1(PID v ∥ ∥ N ORSU i ∥ ∥ rn i),( i= 0,···, n)。

4) TPD 计算 M1 = {E PK CA(E P‖PWD‖IDv ‖S 永久身份v‖公钥 PKv‖Ts1) , H(E PKCA), Ts1}，其中Ts1是时间戳。车载单元将M1发送给证书颁发机构。

5) 证书颁发机构检查Ts1和接收到的H(E PKCA)。如果正确，证书颁发机构使用SKCA解密以获取PWD和IDv。然后，证书颁发机构验证PWD和IDv，并使用循环移位矩阵EP对 H信息进行移位，以获得被加密的循环H信息Einfo。

图3所示示例中，证书颁发机构对矩阵E P的每一行执行幂运算，幂为H信息=[m0,m1, m2,m3]中对应的路侧单元RSU1,RSU2,RSU3, RSU4的第i个值。证书颁发机构将每行中的所有元素相乘以得到Einf o。(6)，如页面底部所示。

6) 将两个向量Einf o和EL的对应元素相乘，根据公式(1)得到Eresult，如等式(7)所示。

Eresult= Einfo × EL =
⎛⎜⎜⎜⎝ gm2 0 hm0r0+m1r1+m2r2+m3r3 gm3 0 hm0r3+m1r0+m2r1+m3r2 gm0 0 hm0r2+m1r3+m2r0+m3r1 gm1 0 hm0r1+m1r2+m2r3+m3r0 ⎞⎟⎟⎟⎠×
⎛⎜⎜⎜⎜⎝ C1 2 C0 3 C1 0 C1 1 ⎞⎟⎟⎟⎟⎠ =
⎛⎜⎜⎜⎜⎝ e(gm2 0 hm0r0+m1r1+m2r2+m3r3, g1 0h r21) hr1 e(g m3 0h r30) hr2 e(g m0 0h r01) hr3 e(g m1 0h r11) hr4 ⎞⎟⎟⎟⎟⎠ =
⎛⎜⎜⎜⎜⎝ g m2 0 h˜r1 g0 0h ˜r2 g m0 0 hr˜3 g m1 0 h˜r4 ⎞⎟⎟⎟⎟⎠ = Eresult (7)

7) 证书颁发机构向车辆发送M2={Eresult, Ts2, S P I Dv,H(E result‖Ts2‖SPIDv)}，其中Ts2为时间戳。

8) 如果Ts2和H(Eresult ‖Ts2‖SPIDv)正确，则车辆接受M2。

9) 车辆使用私钥和波拉德λ算法 [25] 对 Eresult 进行解密，以获取路侧单元（RSUs）的 m2, m0,m1。

(Eresult) q =
⎛⎜⎜⎝ gm2 0 hr˜1 g00hr˜2 gm0 0 hr˜3 gm1 0 hr˜4 ⎞⎟⎟⎠q =
⎛⎜⎜⎝(gm2 0 hr˜1)q (g00hr˜2)q (gm0 0 hr˜3)q (gm1 0 hr˜4)q ⎞⎟⎟⎠=
⎛⎜⎜⎝(gm2 0)q (g00)q (gm0 0)q (gm1 0)q ⎞⎟⎟⎠ =
⎛⎜⎜⎝(g0q)m2 (g0q)0 (g0q)m0 (g0q)m1 ⎞⎟⎟⎠ (8)

10) Vehicle obtains the information {m1:(1 ∥ ∥N ORSU1 ∥ m2 : (2 ∥ ∥N ORSU2 ∥ : (0 ∥ ∥N ORSU0 ∥ of RSUs that will pass.

D. 认证阶段

一旦车辆获得RSU的认证密钥，RSU与车辆的OBU之间即可实现快速认证。

1) TPD 计算临时伪名 SPIDv=H1(PIDv ∥ ∥N ORSU i ∥
2) TPD 计算 M 3 = { KRSUi( || v|| || RSUi‖ s3) v EPID SPID a NOT, SPID, H(EKRSU) ,Ts3}，其中 a 是随机数，Ts3是时间戳，EKRSU是使用密钥 KRSUi的对称加密算法（如高级加密标准）。OBU 将 M3发送给 RSU。
3) RSU 验证 H (EKRSUi) ，然后使用 K RSUi解密接收到的消息以获取 N ORSUi、SPIDv和 a。如果 N ORSUi正确，RSU 对车辆进行认证，并向车辆发送 H (a + 1)。
4) 车辆检查接收到的 H (a +1) 是否正确。如果正确，则认证成功；否则，认证失败。

五、分析

在本节中，对我们的PLVA方案进行了分析，以实现消息完整性、消息机密性、车辆匿名性和路径规划隐私。此外，还从TPD的预计算、证书颁发机构的计算和认证操作方面评估了性能。

A. 安全性分析

• 消息完整性 :
  假设一个攻击者截获并篡改消息M3={EK RSU(永久身份||SPID v||随机数||NORSU i ‖Ts) ,SPIDv, H(EKRSU), Ts3}，然后将修改后的消息发送给接收方。由于等式 H(E′ KRSUi) = H(EKRSUi) 不再成立，因此可以检测到这种攻击。消息完整性得以保证。

• 消息机密性 :
  假设攻击者试图解密窃听的消息，则他需要知道SKv, SKCA和KRSUi。然而，SKv存储在车辆的可信处理设备中，SKCA仅由证书颁发机构知晓，而KRSUi存储在TPD、证书颁发机构和路侧单元中。因此，消息机密性得到保障。

• 身份匿名性 :
  即使所有路侧单元（RSUs）都被攻击者攻破，车辆的真实身份仍然未知，因为路侧单元只知道SPIDv。此外，由于路侧单元中存储的SPIDv由SPIDv=H1(PIDv ∥ ∥ N ORSU i ∥ ∥ rni)构成，在安全哈希函数H的假设下，从该值推导出永久身份 在计算上是不可行的，从而实现了身份匿名性。

• 路径规划隐私 ：
  当车辆向证书颁发机构查询路侧单元的信息时，车辆发送的请求消息是被加密的。如果证书颁发机构想要获取车辆的路线规划，则需要知道车辆的SKv。然而，SKv被假设安全地存储在车辆的可信处理设备中，因此路径规划隐私得到了保护。

B. 性能评估

查询阶段的执行时间随RSU数量的变化而变化。例如，北京市区面积约为1401平方公里，路侧单元（RSUs）的通信距离约为1000 m，每个路侧单元的覆盖面积约为3平方公里，因此覆盖北京市大约需要500个RSU。在一些拥堵区域，需要更多的路侧单元，我们假设RSU最大数量为1000。向量中的每个元素代表一个路侧单元，仿真为使用配备英特尔 i5‐8300H 2.3GHz、16G 内存的笔记本电脑执行。此外，查询阶段使用 JAVA 实现。代码可在以下网站下载：https://github.com/secureldata/privacy‐preserving‐and‐lightweight‐V2I‐authentication‐PLVA‐protocol。

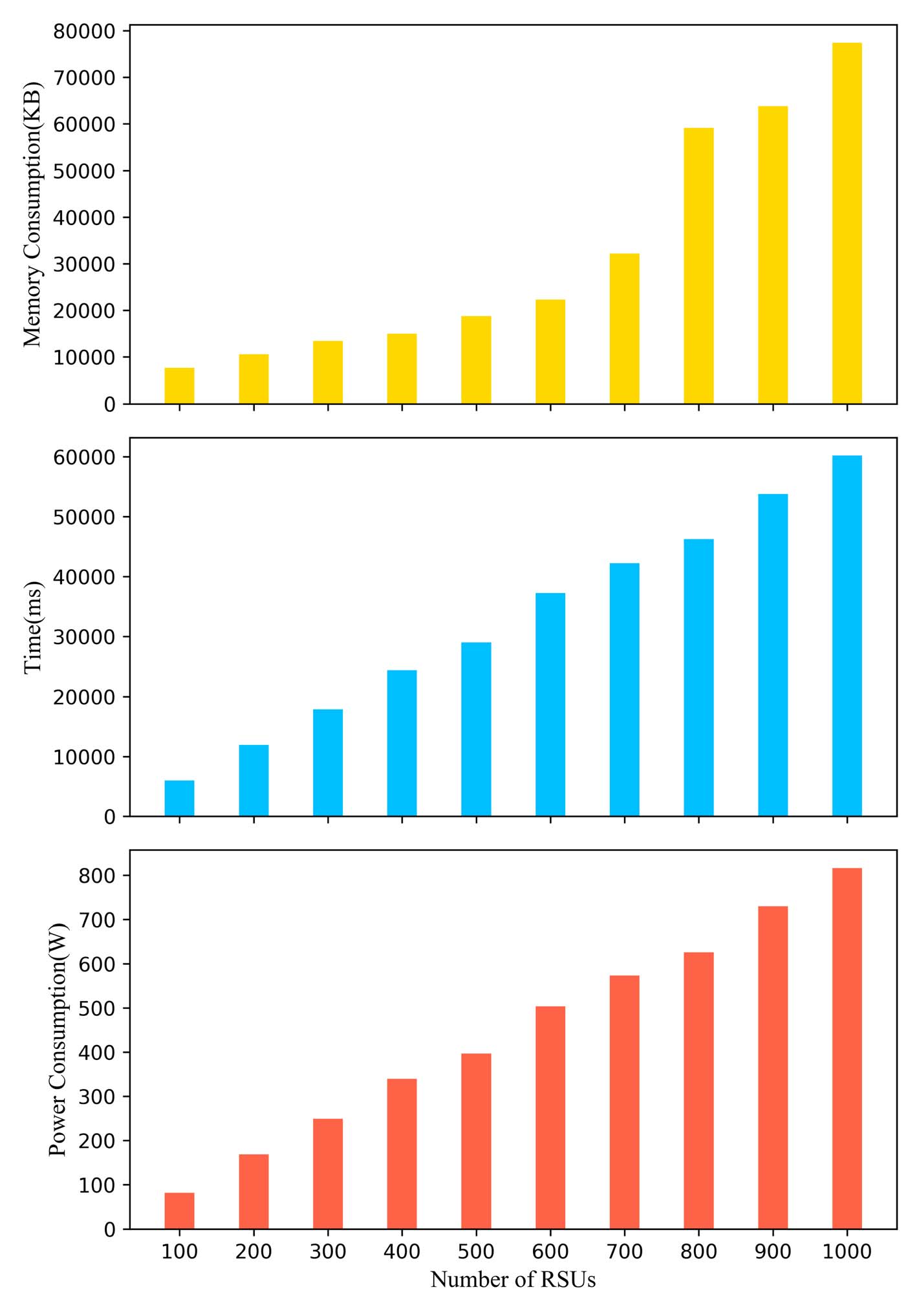
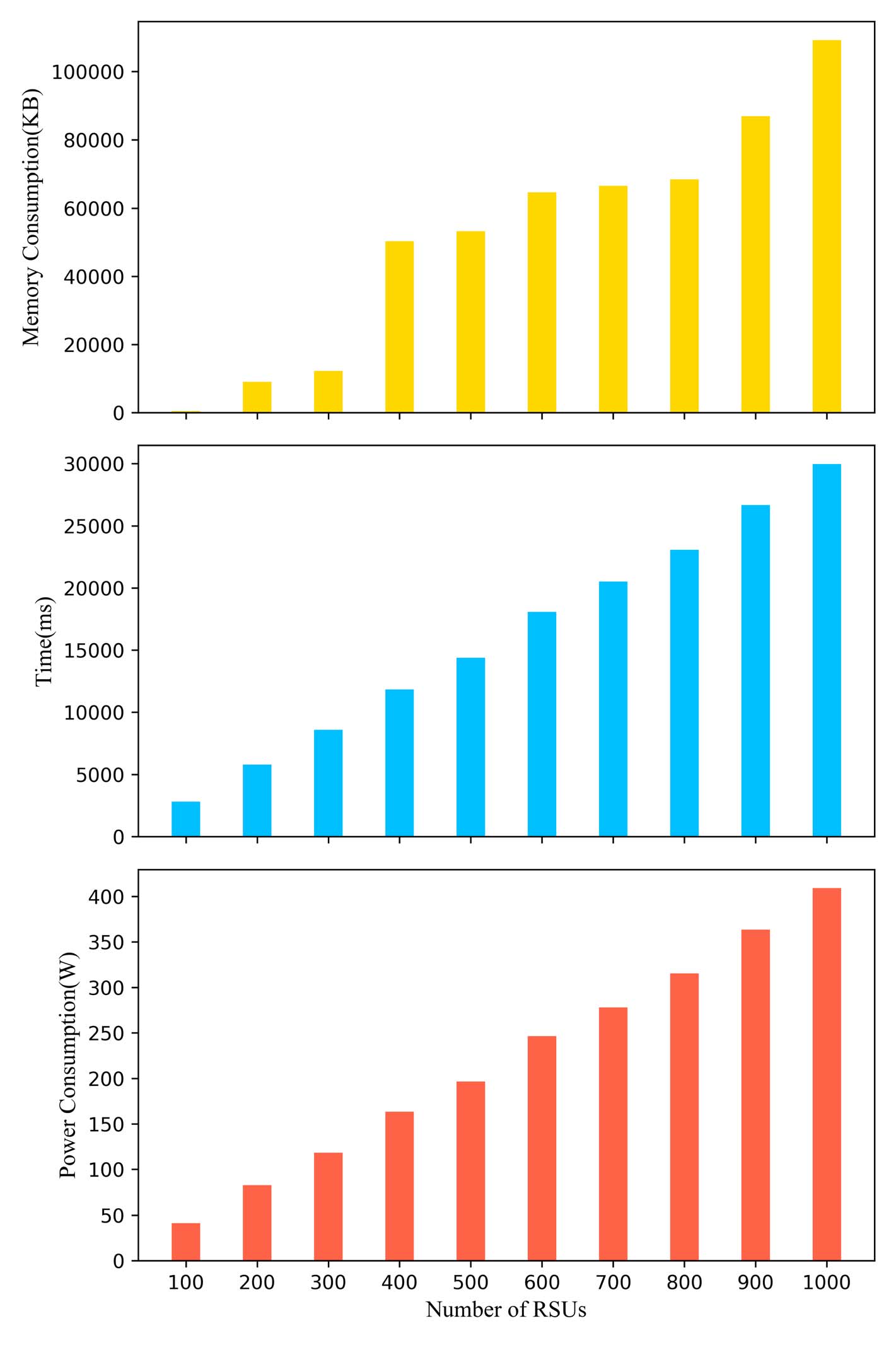
1) TPD 计算列表 L 中每个元素的两个加密值 C0 i= g 0 0 hri 和 C1 i= g 1 0h ri。执行时间、内存消耗和功耗如图4所示。

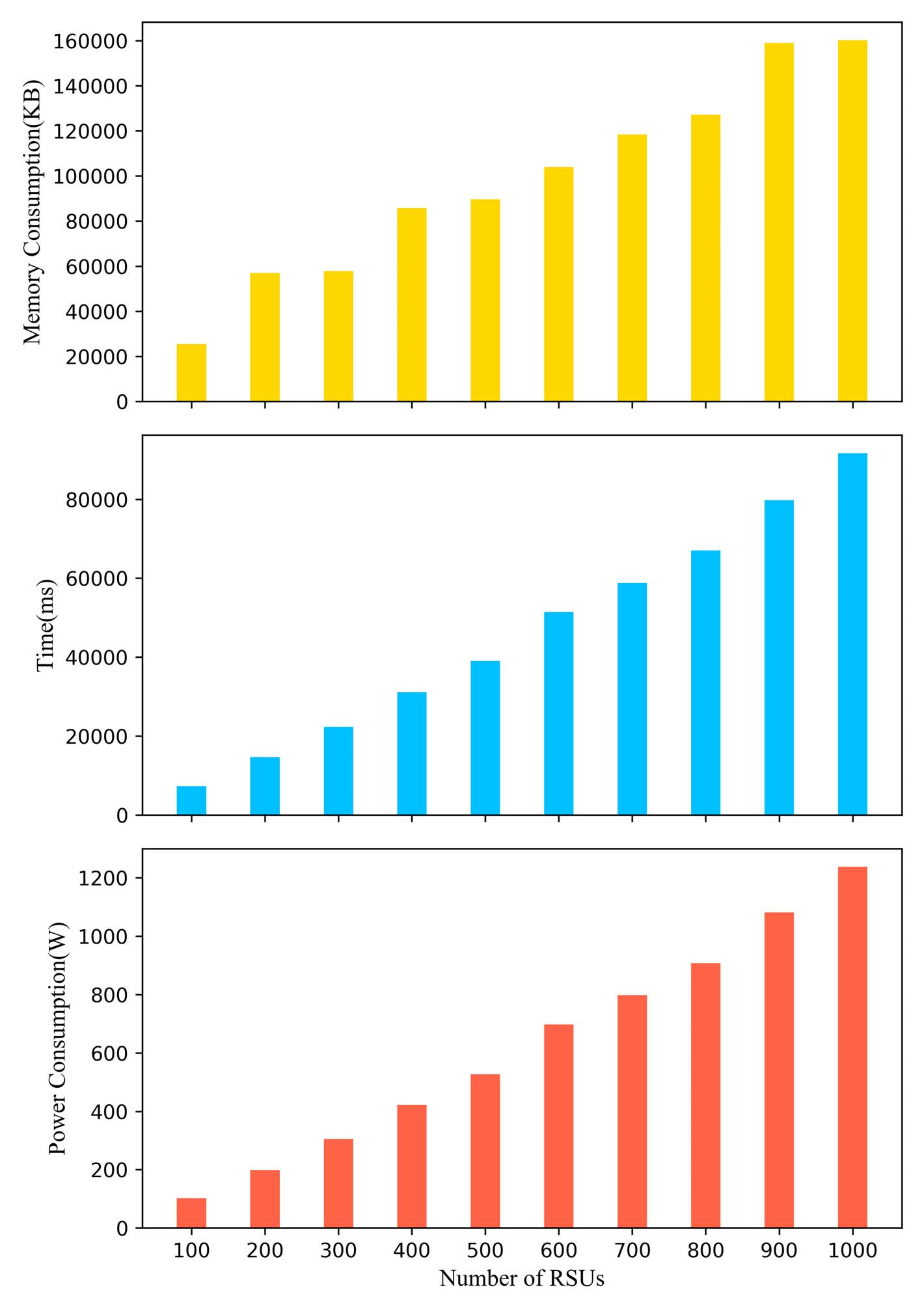
2) 当TPD计算加密循环移位矩阵时，只需计算加密循环移位矩阵的第一行，其余行通过连续移位第一行获得。在此过程中，TPD计算一个循环移位矩阵P的计算开销如图5所示。

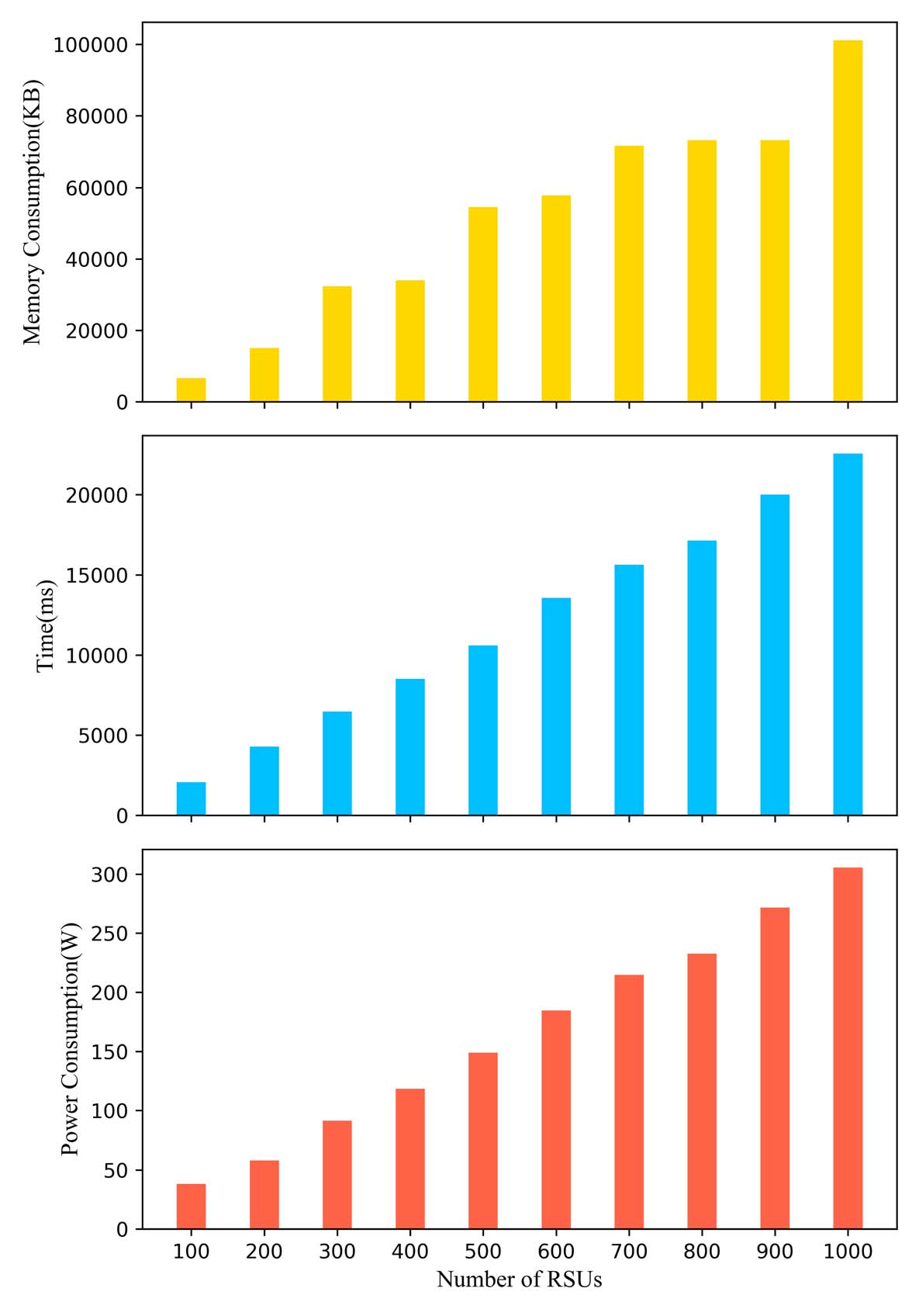
3) 证书颁发机构需要对加密循环移位矩阵EP中的每个元素执行一次幂运算，并将加密循环移位矩阵中每一行的元素相乘，以获得移位后的加密结果Einf o。最后，证书颁发机构使用BGN同态乘法将Einf o和EL相乘，得到最终结果Eresult。证书颁发机构为获得最终结果Eresult的计算开销如图6所示。

4) TPD解密结果的计算开销如图7所示。在认证阶段，我们的PLVA方案与LVAP [18]、曾氏方案 [17]、EAAP [14]、和朱氏方案 [16]进行了比较。LVAP的效率依赖于对称密码学，曾氏方案依赖于基于批处理的验证，而EAAP则基于证书签名验证，同时，朱氏方案通过身份签名验证得以保证。

符号列表见表I。

在表II中，我们比较了LVAP、EAAP、朱氏方案、曾氏方案和PLVA在认证阶段的验证时间。

认证仿真如图8所示。PLVA性能优于LVAP、EAAP、朱氏方案和曾氏方案，特别是当攻击者发送篡改消息以降低批量验证效率时，PLVA比曾氏方案更高效。

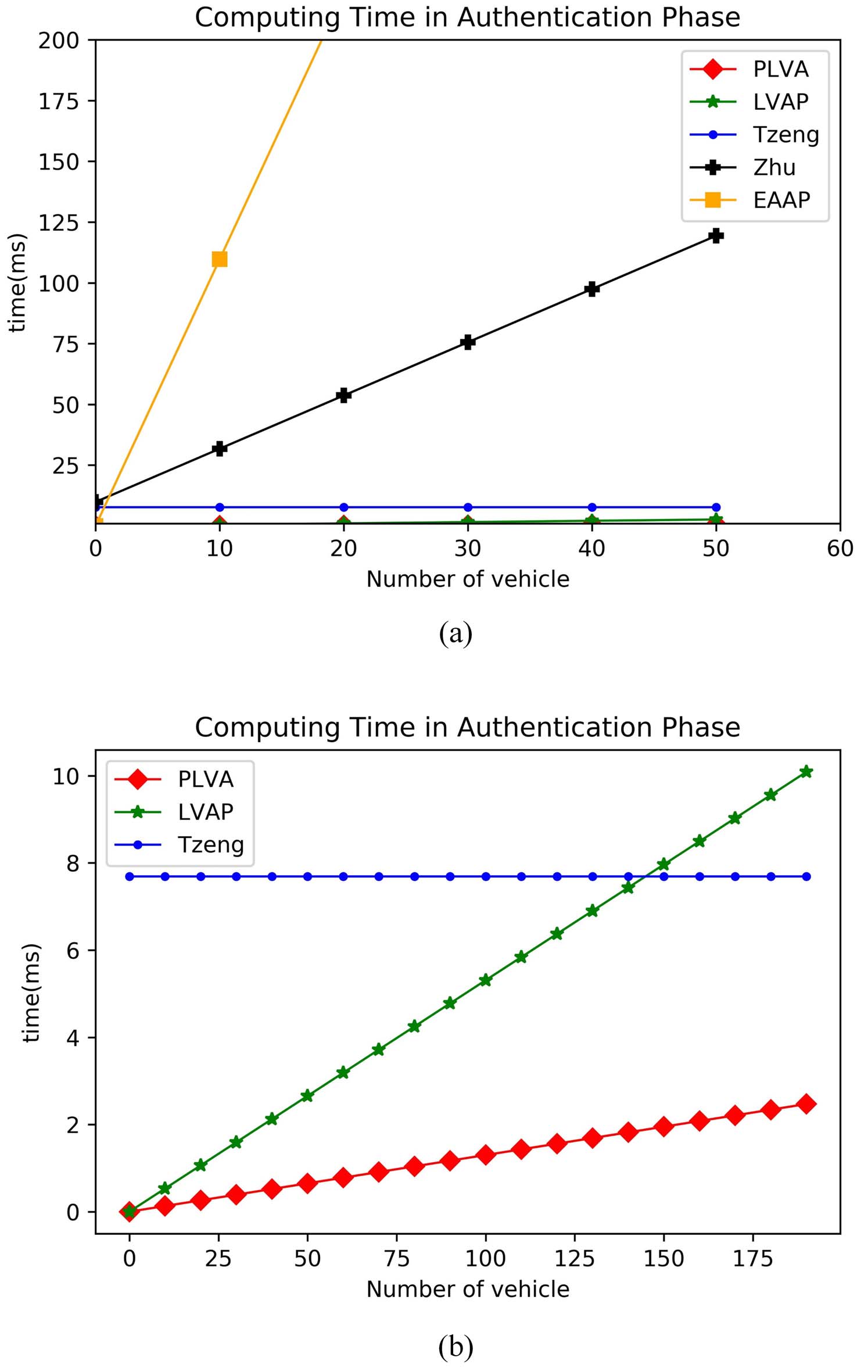中，比较了LVAP、曾氏方案、EAAP、朱氏方案和PLVA在认证阶段的执行时间。在图8(b)中，由于LVAP、曾氏方案和PLVA方案的曲线在图8(a)中几乎重合，因此进行了放大显示)

VI. 结论

在实际应用中，认证效率极大地影响着用户体验。特别是在车载自组织网络（VANET）中，由于车辆高速移动，认证效率不仅关系到信息安全，还直接影响驾驶员生命安全。如果能够在车辆路径上的车辆与路侧单元之间预先执行一些预计算以共享必要消息，则可显著提高认证速度。

为解决预计算可能泄露车辆路线规划的担忧，我们提出了PLVA。未来仍有一些开放性问题需要研究。例如，PLVA在认证前使用BGN同态加密算法，该算法保证了车辆的隐私和计算效率。然而，随着RSU数量的增加，开销将持续增长。因此，在大范围区域应用时，我们的PLVA仍需进一步改进。