卡诺图 最大项

国内的教材只介绍了卡诺图最小项，下面的资料介绍了卡诺图的最大项 Maxterm

http://www.allaboutcircuits.com/vol_4/chpt_8/8.html

A maxterm is a Boolean expression resulting in a 0 for the output of a single cell expression, and 1s for all other cells in the Karnaugh map, or truth table. The illustration above left shows the maxterm (A+B+C), a single sum term, as a single 0 in a map that is otherwise 1s. If a maxterm has a single 0 and the remaining cells as 1s, it would appear to cover a maximum area of 1s.

There are some differences now that we are dealing with something new, maxterms. The maxterm is a 0, not a 1 in the Karnaugh map. A maxterm is a sum term, (A+B+C) in our example, not a product term.

It also looks strange that (A+B+C) is mapped into the cell 000. For the equation Out=(A+B+C)=0, all three variables (A, B, C) must individually be equal to 0. Only (0+0+0)=0 will equal 0. Thus we place our sole 0 for minterm (A+B+C) in cell A,B,C=000 in the K-map, where the inputs are all0 . This is the only case which will give us a 0 for our maxterm. All other cells contain 1s because any input values other than ((0,0,0) for (A+B+C) yields 1s upon evaluation.

Referring to the above figure, the procedure for placing a maxterm in the K-map is:

• Identify the Sum term to be mapped.
• Write corresponding binary numeric value.
• Form the complement
• Use the complement as an address to place a 0 in the K-map
• Repeat for other maxterms (Sum terms within Product-of-Sums expression).

Another maxterm A'+B'+C' is shown above. Numeric 000 corresponds to A'+B'+C'. The complement is 111. Place a 0 for maxterm (A'+B'+C')in this cell (1,1,1) of the K-map as shown above.

Why should (A'+B'+C') cause a 0 to be in cell 111? When A'+B'+C' is (1'+1'+1'), all 1s in, which is (0+0+0) after taking complements, we have the only condition that will give us a 0. All the 1s are complemented to all 0s, which is 0 when ORed.

A Boolean Product-Of-Sums expression or map may have multiple maxterms as shown above. Maxterm (A+B+C) yields numeric 111 which complements to 000, placing a 0 in cell (0,0,0). Maxterm (A+B+C') yields numeric 110 which complements to 001, placing a 0 in cell (0,0,1).

Now that we have the k-map setup, what we are really interested in is showing how to write a Product-Of-Sums reduction. Form the 0s into groups. That would be a group of two below. Write the binary value corresponding to the sum-term which is (0,0,X). Both A and B are 0 for the group. But, C is both 0 and 1 so we write an X as a place holder for C. Form the complement (1,1,X). Write the Sum-term (A+B) discarding the C and the X which held its' place. In general, expect to have more sum-terms multiplied together in the Product-Of-Sums result. Though, we have a simple example here.

Let's summarize the procedure for writing the Product-Of-Sums Boolean reduction for a K-map:

• Form largest groups of 0s possible, covering all maxterms. Groups must be a power of 2.
• Write binary numeric value for group.
• Complement binary numeric value for group.
• Convert complement value to a sum-term.
• Repeat steps for other groups. Each group yields a sum-term within a Product-Of-Sums result.

Example:

Simplify the Product-Of-Sums Boolean expression below, providing a result in POS form.

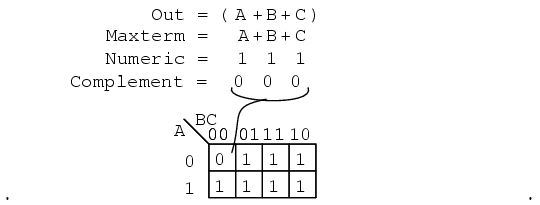
A maxterm is a Boolean expression resulting in a 0 for the output of a single cell expression, and 1s for all other cells in the Karnaugh map, or truth table. The illustration above left shows the maxterm (A+B+C), a single sum term, as a single 0 in a map that is otherwise 1s. If a maxterm has a single 0 and the remaining cells as 1s, it would appear to cover a maximum area of 1s.

There are some differences now that we are dealing with something new, maxterms. The maxterm is a 0, not a 1 in the Karnaugh map. A maxterm is a sum term, (A+B+C) in our example, not a product term.

It also looks strange that (A+B+C) is mapped into the cell 000. For the equation Out=(A+B+C)=0, all three variables (A, B, C) must individually be equal to 0. Only (0+0+0)=0 will equal 0. Thus we place our sole 0 for minterm (A+B+C) in cell A,B,C=000 in the K-map, where the inputs are all0 . This is the only case which will give us a 0 for our maxterm. All other cells contain 1s because any input values other than ((0,0,0) for (A+B+C) yields 1s upon evaluation.

Referring to the above figure, the procedure for placing a maxterm in the K-map is:

• Identify the Sum term to be mapped.
• Write corresponding binary numeric value.
• Form the complement
• Use the complement as an address to place a 0 in the K-map
• Repeat for other maxterms (Sum terms within Product-of-Sums expression).

Another maxterm A'+B'+C' is shown above. Numeric 000 corresponds to A'+B'+C'. The complement is 111. Place a 0 for maxterm (A'+B'+C')in this cell (1,1,1) of the K-map as shown above.

Why should (A'+B'+C') cause a 0 to be in cell 111? When A'+B'+C' is (1'+1'+1'), all 1s in, which is (0+0+0) after taking complements, we have the only condition that will give us a 0. All the 1s are complemented to all 0s, which is 0 when ORed.

A Boolean Product-Of-Sums expression or map may have multiple maxterms as shown above. Maxterm (A+B+C) yields numeric 111 which complements to 000, placing a 0 in cell (0,0,0). Maxterm (A+B+C') yields numeric 110 which complements to 001, placing a 0 in cell (0,0,1).

Now that we have the k-map setup, what we are really interested in is showing how to write a Product-Of-Sums reduction. Form the 0s into groups. That would be a group of two below. Write the binary value corresponding to the sum-term which is (0,0,X). Both A and B are 0 for the group. But, C is both 0 and 1 so we write an X as a place holder for C. Form the complement (1,1,X). Write the Sum-term (A+B) discarding the C and the X which held its' place. In general, expect to have more sum-terms multiplied together in the Product-Of-Sums result. Though, we have a simple example here.

Let's summarize the procedure for writing the Product-Of-Sums Boolean reduction for a K-map:

• Form largest groups of 0s possible, covering all maxterms. Groups must be a power of 2.
• Write binary numeric value for group.
• Complement binary numeric value for group.
• Convert complement value to a sum-term.
• Repeat steps for other groups. Each group yields a sum-term within a Product-Of-Sums result.

Example:

Simplify the Product-Of-Sums Boolean expression below, providing a result in POS form.

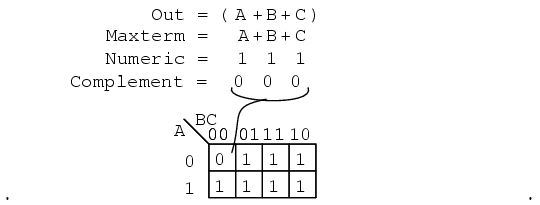
A maxterm is a Boolean expression resulting in a 0 for the output of a single cell expression, and 1s for all other cells in the Karnaugh map, or truth table. The illustration above left shows the maxterm (A+B+C), a single sum term, as a single 0 in a map that is otherwise 1s. If a maxterm has a single 0 and the remaining cells as 1s, it would appear to cover a maximum area of 1s.

There are some differences now that we are dealing with something new, maxterms. The maxterm is a 0, not a 1 in the Karnaugh map. A maxterm is a sum term, (A+B+C) in our example, not a product term.

It also looks strange that (A+B+C) is mapped into the cell 000. For the equation Out=(A+B+C)=0, all three variables (A, B, C) must individually be equal to 0. Only (0+0+0)=0 will equal 0. Thus we place our sole 0 for minterm (A+B+C) in cell A,B,C=000 in the K-map, where the inputs are all0 . This is the only case which will give us a 0 for our maxterm. All other cells contain 1s because any input values other than ((0,0,0) for (A+B+C) yields 1s upon evaluation.

Referring to the above figure, the procedure for placing a maxterm in the K-map is:

• Identify the Sum term to be mapped.
• Write corresponding binary numeric value.
• Form the complement
• Use the complement as an address to place a 0 in the K-map
• Repeat for other maxterms (Sum terms within Product-of-Sums expression).

Another maxterm A'+B'+C' is shown above. Numeric 000 corresponds to A'+B'+C'. The complement is 111. Place a 0 for maxterm (A'+B'+C')in this cell (1,1,1) of the K-map as shown above.

Why should (A'+B'+C') cause a 0 to be in cell 111? When A'+B'+C' is (1'+1'+1'), all 1s in, which is (0+0+0) after taking complements, we have the only condition that will give us a 0. All the 1s are complemented to all 0s, which is 0 when ORed.

A Boolean Product-Of-Sums expression or map may have multiple maxterms as shown above. Maxterm (A+B+C) yields numeric 111 which complements to 000, placing a 0 in cell (0,0,0). Maxterm (A+B+C') yields numeric 110 which complements to 001, placing a 0 in cell (0,0,1).

Now that we have the k-map setup, what we are really interested in is showing how to write a Product-Of-Sums reduction. Form the 0s into groups. That would be a group of two below. Write the binary value corresponding to the sum-term which is (0,0,X). Both A and B are 0 for the group. But, C is both 0 and 1 so we write an X as a place holder for C. Form the complement (1,1,X). Write the Sum-term (A+B) discarding the C and the X which held its' place. In general, expect to have more sum-terms multiplied together in the Product-Of-Sums result. Though, we have a simple example here.

Let's summarize the procedure for writing the Product-Of-Sums Boolean reduction for a K-map:

• Form largest groups of 0s possible, covering all maxterms. Groups must be a power of 2.
• Write binary numeric value for group.
• Complement binary numeric value for group.
• Convert complement value to a sum-term.
• Repeat steps for other groups. Each group yields a sum-term within a Product-Of-Sums result.

Example:

Simplify the Product-Of-Sums Boolean expression below, providing a result in POS form.