【组合数】模板

题目

活动 - AcWing

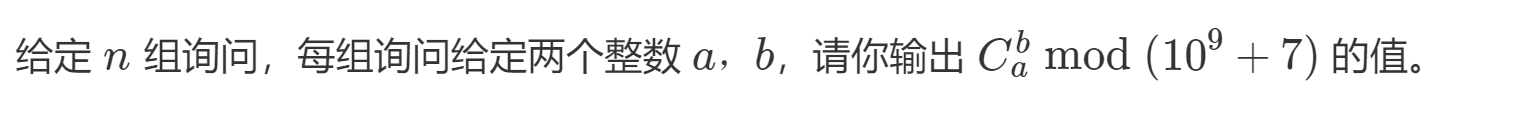
解释

• 初始化所有c[i][0]情形
• 递推公式思想为假设有a个苹果，则选择b个苹果的方案数可以看成是
• 不选择第i个苹果，则方案数为C(a-1,b)
• 选择第i个苹果，则方案数为C(a-1,b-1)

代码段

#include<iostream>
using namespace std;
const int N=2010,mod=1e9+7;
long long c[N][N];
void init()
{
    for(int i=0;i<N;i++)
    for(int j=0;j<=i;j++)
    {
        if(!j)c[i][j]=1;
        else
        c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
    }
}
int main()
{
    init();
    int n;
    cin>>n;
    while(n--)
    {
        int a,b;
        cin>>a>>b;
        cout<<c[a][b]<<endl;
    }
}