【离散数学】图论

最新推荐文章于 2025-04-26 22:30:45 发布

Nathan Qian

最新推荐文章于 2025-04-26 22:30:45 发布

阅读量1.7w

点赞数 9

分类专栏：离散数学文章标签：数学

本文链接：https://blog.youkuaiyun.com/nathanqian123/article/details/121376985

版权

离散数学专栏收录该内容

2 篇文章

订阅专栏

无向图与有向图

定义

1.无向图G是二元组<V,E>

(1) 顶点集V是非空有穷集合 ,其元素称为顶点.

(2) 边集E为V&V的多重子集，其元素称为无向边，简称边.

2.有向图D是二元组<V,E>

(1)顶点集V是非空有穷集合, 其元素称为顶点.

(2) 边集E为V´V的多重子集，其元素称为有向边，简称边.

D的基图:用无向边代替有向边

特殊的图

N阶图：n个顶点的图

零图：一条边也没有的图

平凡图：一阶零图

顶点与边的关联与相邻

关联：

设e=(u,v)是无向图G=<V,E>的一条边, 称u,v为e的端点, e与u ( v)关联.

若u≠v, 则称e与u ( v)的关联次数为1;

若u=v, 则称e为环, 此时称e与u 的关联次数为2;

若w不是e端点, 则称e与w 的关联次数为0. 无边关联的顶点称作孤立点.

相邻分为：边的相邻与端点的相邻

相邻：

设无向图G=<V,E> u,v∈V, e,e'∈E, 若(u,v)∈E, 则称u,v相邻;

若e,e'至少有一个公共端点, 则称e,e'相邻.

对有向图有类似定义. 设e=<u,v>是有向图的一条边,又称u是e的始点, v是e的终点

u邻接到v, v邻接于u.

V1为e1的始点

V2为e1的终点

对于e1和e5两边，e1的终点是e5的起点

无向图和有向图的度数

无向图的度数：顶点v作为边的端点的次数，记作d(v)

有向图的度数：

出度：顶点v作为边的始点的次数，记作d+(v)

入度：顶点v作为边的终点的次数，记作d-(v)

总度数d(v)=出度+入度=d+(v)+d-(v)

握手定理

在任何无向图中，所有顶点的度数之和等于边数的两倍
在任何有向图中，所有顶点的度数之和等于边数的两倍
所有顶点的入度之和等于所有顶点的出度之和，等于边数

推论：

任何图中，奇度顶点个数是偶数

度数之和=奇度顶点的度数之和+偶度顶点的度数之和

证明：

由于顶点的度数之和是边数的两倍，所以顶点度数之和是个偶数

由于偶度顶点度数之和也是偶数

所以奇度顶点度数之和也是偶数

度数列

N阶无向图

度数列：d(v1),d(v2),….,d(vn) d=(d1,d2,…,dn)

N阶有向图

出度列和入度列

例题

可图化

可图化的意思是度数列可以由图来表示

可图化的要求为

度数之和为偶数
顶点的最大度数小于等于n-1

最大度和最小度

例题：

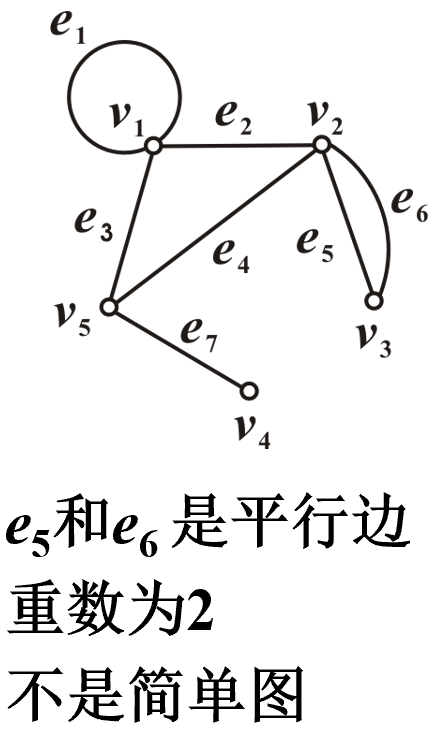
多重图与简单图

平行边：

在无向图中,如果有2条或2条以上的边关联同一对顶点, 则称这些边为平行边, 平行边的条数称为重数.

在有向图中,如果有2条或2条以上的边具有相同的始点和终点, 则称这些边为有向平行边, 简称平行边, 平行边的条数称为重数.

含平行边的图称为多重图. 既无平行边也无环的图称为简单图.

无向完全图与有向完全图

n阶无向简单图:每个顶点都与其余顶点相邻的n阶无向简单图.记作kn

边数m=n(n-1)/2

n阶有向完全图：每对顶点之间均有两条方向相反的有向边的n阶有向简单图.

边数m=n(n-1)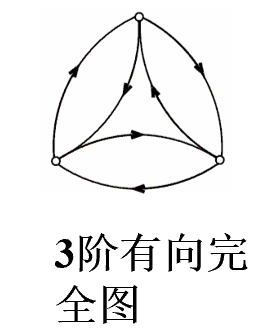

子图与补图

设G=<V,E>,G'=<V',E'>是两个图

子图

生成子图

补图

设G=<V,E>为n阶无向简单图，以V为顶点集,所有使G成为完全图Kn的添加边组成的集合为边集的图，称为G的补图

通路与回路

定义

通路：无向图G中顶点与边的交替序列

Vi0=VIL,则称Γ为回路

图的连通性

设无向图G=<V,E>若u,v∈V之间存在通路，则称u,v是连通的，记作u~v

规定：任意v∈V，v~v

连通图

若无向图G是平凡图或G中任意两个顶点都是连通的，则称为连通图

可达

有向图G=<V,E>,对u，v∈V，若从u到v存在通路，则称u到v是可达的，若从u到v存在通路，且从v到u存在通路，则称u和v相互可达

几种连通

强连通：任意两个结点间是相互可达的

单向连通：任意两个结点至少从一个结点到另一个结点是可达的

弱连通的：在略去有向边的方向后得到的无向图是连通的

图的矩阵表示

无向图的矩阵表示

设无向图G=<V,E>, V={v1, v2, …, vn}, E={e1, e2, …, em}, 令mij为vi与ej的关联次数，

称(mij)n*m为G的关联矩阵，记为M(G)

mij=

2 vi = vj
1 vi != vj
0

顶点V为行数，边e为列数

有向图的矩阵表示

设无环有向图D=<V,E>, V={v1, v2, …, vn}, E={e1, e2, …, em}

mij=

1 vi为ej的始点
0 vi为ej不关联
-1 vi是ej的终点

有向图的邻接矩阵

设有向图D=<V,E>, V={v1, v2, …, vn}, E={e1, e2, …, em}

令aij(1)为顶点vi邻接到顶点vj边的条数

称(aij（1）)n*n为D的邻接矩阵, 记作A(D), 简记为A.

有向图的通路总数及回路总数

根据矩阵表示找vi到vj长度为 l 的通路条数和回路条数

例题

有向图的可达矩阵

设D=<V,E>为有向图，V={v1,v2,……,v3,vn}

pij=

1 vi可达vj
0 vi不可达vj

称(pij)n*n为D的可达矩阵，记作P(D),简记为P

欧拉图

定义

欧拉通路: 图中行遍所有顶点且恰好经过每条边一次的通路.
欧拉回路: 图中行遍所有顶点且恰好经过每条边一次的回路.
欧拉图: 有欧拉回路的图.
半欧拉图: 有欧拉通路回路,但无欧拉回路的图.

判别法

无向图G是欧拉图当且仅当G是连通图且没有奇度顶点
有向图D是欧拉图当且仅当D是强连通图（任意两个顶点可达）且每个顶点的入度等于出度

哈密顿图

定义

哈密顿通路：经过图中所有顶点一次且仅一次的通路

哈密顿回路：经过图中所有顶点一次且仅一次的回路

哈密顿图：具有哈密顿回路的图

半哈密顿图：具有哈密顿通路但不具有哈密顿回路的图

判断条件

设G是n阶无向简单图，若对于G中任意不相邻的顶点u,v；均有d(u)+d(v)>=n-1

则G中存在哈密顿通路

设G是n(n>=3)阶无向简单图，若对于G中任意不相邻的顶点u,v均有d(u)+d(v)>=n

则G中存在哈密顿回路

最短路问题

权，带权图

最短路径

在带权图中，任意u,v∈V。当u和v连通的时候，从u到v的长度最短得路径称其长度为从u到v的距离，记作d(u,v)

d(u,u)=0

当u和v不相邻时，d(u,v)=+∞

最短路问题

基于迪杰斯特拉算法思想（实际上是一个贪心算法）

带权图=<V,E,W>及顶点u和v，求从u到v的最短路径

求解步骤

建议参考视频：

图论最短距离

首先列出表格

列数为1 先初始化表格 v1到v1为0 其他一律记为+∞

然后寻找这一列的最短路径，记录这个值并且省去查找后面的操作（划斜杠）

列数为2 以v1为顶点相邻顶点记录距离不相邻的依旧记+∞

然后寻找这一列的最短路径，记录这个值并且省去这一行查找后面的操作（划斜杠）

列数为3 以v2为顶点相邻顶点记录距离不相邻的依旧记+∞

类推

时间复杂度为O(N*N)

二部图

定义

所有边都在u,v之间
u之间没有边
v之间没有边

判定二部图

程序判定法：

步骤：

任意选择一个节点，并将它染成红色
重复执行如下操作:
将红色节点的邻近节点染成蓝色
蓝色节点的临近节点染成红色
如果有一个节点的和它的邻近节点颜色相同则不是二部图

一般判定法：

无向图G=<V,E>是二部图当且仅当G中无奇圈（奇圈即是长度为奇数的回路）。

（所有回路的长度均为偶数）

平凡图和零图是特殊的二部图

或根据定义来识别