概率与数学期望例题——uva11722（图形面积与概率）

Yuki_nan

于 2018-04-24 19:06:52 发布

阅读量1.6k

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/nan81962325/article/details/80068678

这篇博客探讨了在不确定的火车到达时间下，计算两位朋友在A市相遇概率的问题。根据输入的数据，包括两个时间区间[t1, t2]和[s1, s2]，以及火车停留时间w，通过分析相遇时间x-y≤w的条件，计算出相遇的几何概率。文章提到了可能的情况，如截取的概率区域可能是梯形或平行四边形，并建议手绘图辅助理解。最终给出了计算概率的代码实现。" 108097968,8260394,算法详解：蓝桥杯竞赛攻略,"['算法竞赛', '数据结构', '动态规划', '数论', 'C++']

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Joining with Friend UVa11722

PDF

首先我们当然看一下原题。

中文翻译：你和朋友都要坐火车，并且都会经过A市，你们很像会面，但是你们到达这个城市的准确时间无法确定。你会在时间区段[t1,t2],中的忍一时可以相同的概率密度到达，你的朋友则会在[s1,s2]中的任意时刻到达，你们的火车会在A市停留w分钟。

输入格式：第一行为数据组数T，接下来的T行每行包含5个整数，分别为t1.t2.s1,s2,w;

输出格式：对于每一组数据，输出会面成功的概率；

假设x，y是两辆火车到达城市A的时间，则整个概率是空间上的一个矩形，则两人相遇的时间是x-y<=W.

因此你的相遇面积为y=x+w与y=x-w截取整个概率面积的多边形；

因此我们需要讨论多种情况，这个线交概率矩形的那一条边，进行相应的计算，有的截出来是梯形，有的是平行四边形；

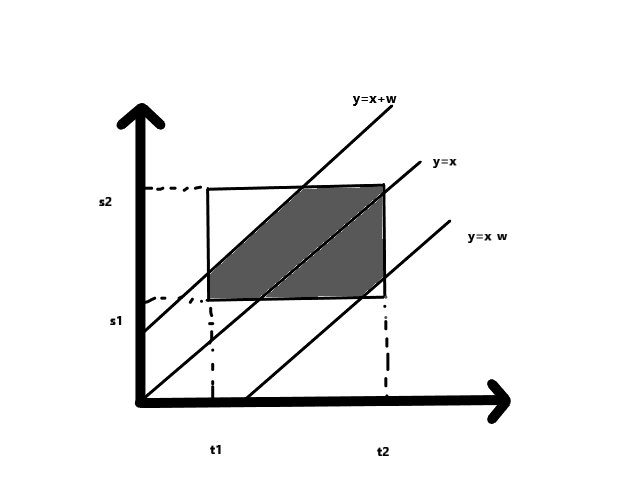
手绘图。。。。

所以上代码：

#include<cstdio>  
#include<algorithm>  
using namespace std;  
int T;
int main(){
    scanf("%d",&T);  
    for(int i=1;i<=T;i++){  
        int edge[10],t1,t2,s1,s2,w,x,y,p;  
        double s