20轴足球魔方

目录

魔方三要素

（1）组成部件

（2）可执行操作

（3）目标态

复原方法

（1）复原1个六边形面

（2）复原起始面周边的3个六边形面

（3）复原起始面周边的3个五边形面

（4）复原这3个五边形面周围的6个六边形面

（5）复原3个五边形面

（6）复原这3个五边形面周围的6个六边形面和另外3个五边形面

（7）调整对立面的朝向

（8）复原最后3个棱块的朝向

（9）复原最后3个棱块的位置

---

魔方三要素

（1）组成部件

足球的性质参考拓扑几何学

足球魔方有20个三角形中心块（包含3个小三角形）、12个五边形中心块、30个棱块

一共有20个六边形面，每个六边形面由1个三角形中心块+3个棱块组成

一共有12个五边形面，每个五边形面由1个五边形中心块+5个棱块+5个中心块的小三角形组成。

（2）可执行操作

20个六边形面，每个六边形面可以旋转120度，所以一共是20个轴，有20种操作。

五边形面无法旋转。

（3）目标态

32个面都是纯色

复原方法

（1）复原1个六边形面

我们用有字的这一面作为起始面

（2）复原起始面周边的3个六边形面

（3）复原起始面周边的3个五边形面

（4）复原这3个五边形面周围的6个六边形面

（5）复原3个五边形面

（6）复原这3个五边形面周围的6个六边形面和另外3个五边形面

前6步一共涉及25个面，顺序其实就是从内到外：

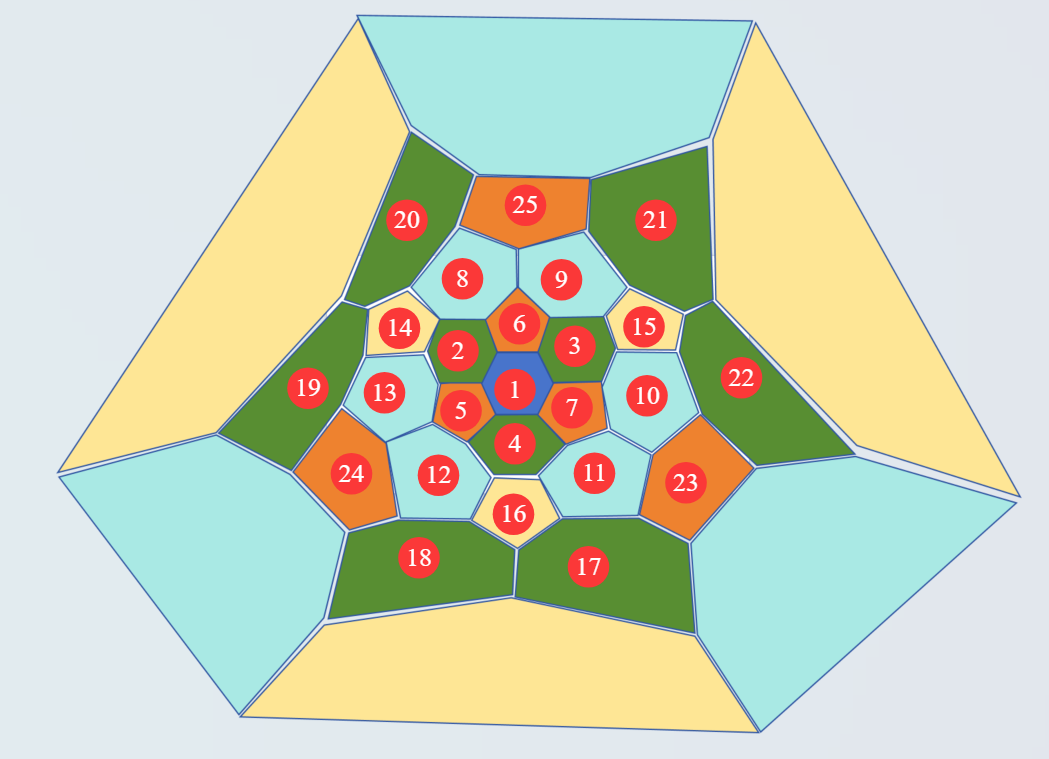
此时，还剩下起始面的对立面及其周围的6个面。

（7）调整对立面的朝向

把对立面旋转到合适的角度，就只差对立面的3个棱块需要复原了。

（8）复原最后3个棱块的朝向

不管棱块的位置，只根据对立面色块判断朝向是正的还是反的。

如果是2个棱的朝向有问题：

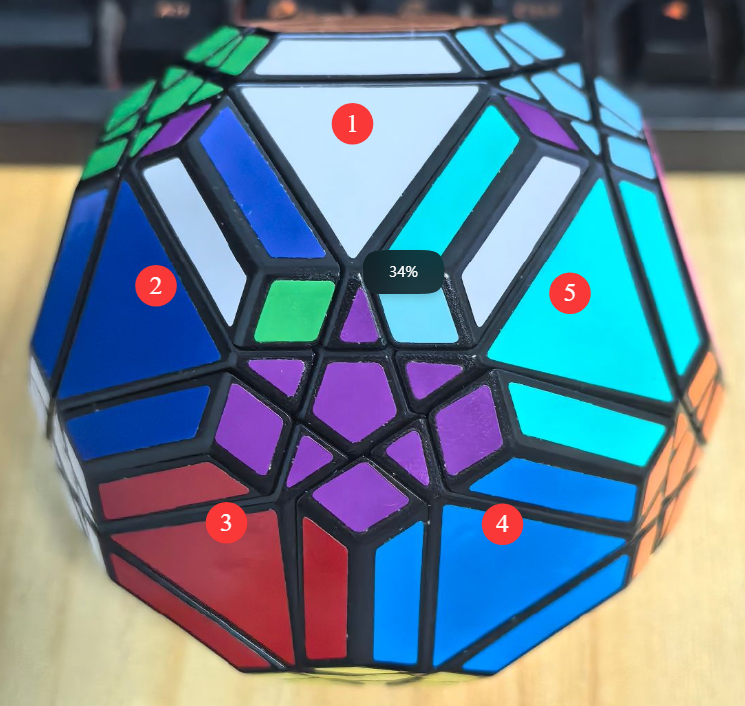
我们用公式1234515544331122（每个面旋转120度）

就可以把这2个棱块的方向调整过来

最后有没有可能出现只有1个棱块朝向是反的呢？应该不可能。

（9）复原最后3个棱块的位置

我们用公式：左右左右右左右左右右左左（都是顺时针旋转120度）

这个公式就是让左边的六边形面的3个棱互换位置。

有了这个公式，就可以让至少1个棱块的位置复原。

此时，另外2个棱块要么位置互换，要么都在正确的位置。

那么，有没有可能2个棱块位置互换呢？

我尝试用三染色的方式去证明不可能存在这种情况，但是并没有证出来。

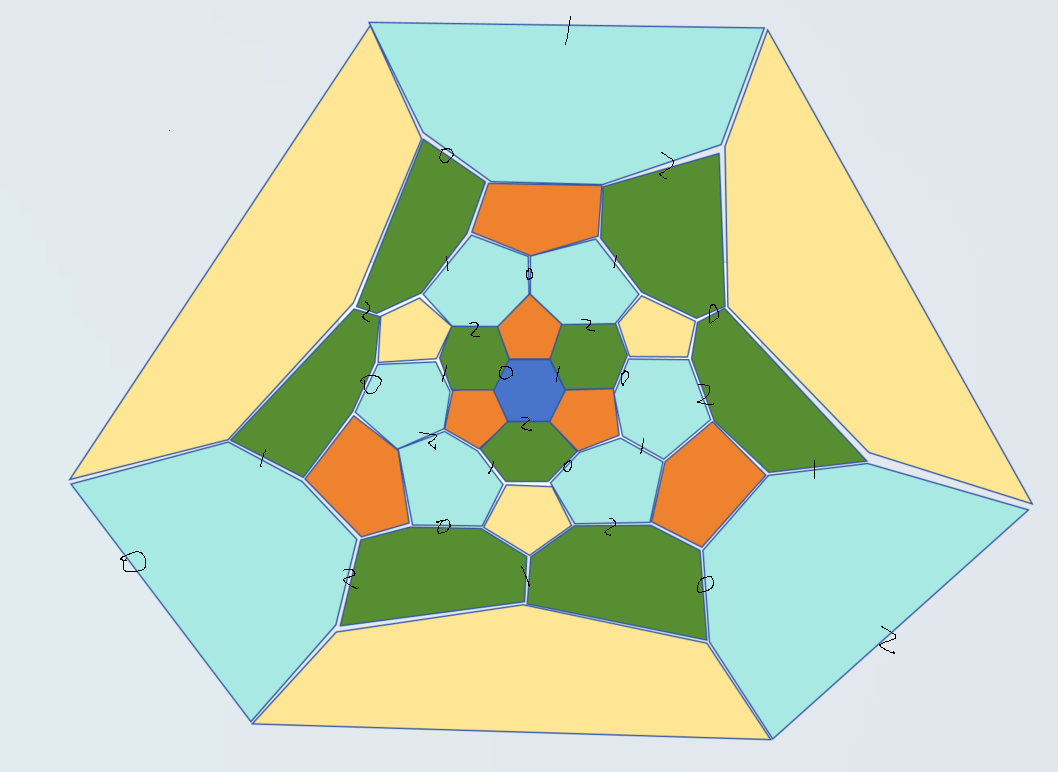
不过，我还是觉得，这种情况应该是不存在的。

至此，魔方复原。