动态规划 # 树型dp问题，没有上司的舞会

原创已于 2024-12-16 19:34:05 修改 · 445 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划 #算法

于 2024-12-16 19:28:07 首次发布

动态规划专栏收录该内容

14 篇文章

订阅专栏

题目解读

题目描述

N 个职员，编号1~N
他们的关系就像一棵以校长为根的树，父节点就是子节点的直接上司。
每个职员有一个快乐指数，用整数 Hi 给出

邀请若干人员，如果邀请了A，则不能邀请A的直接上司

样例计算

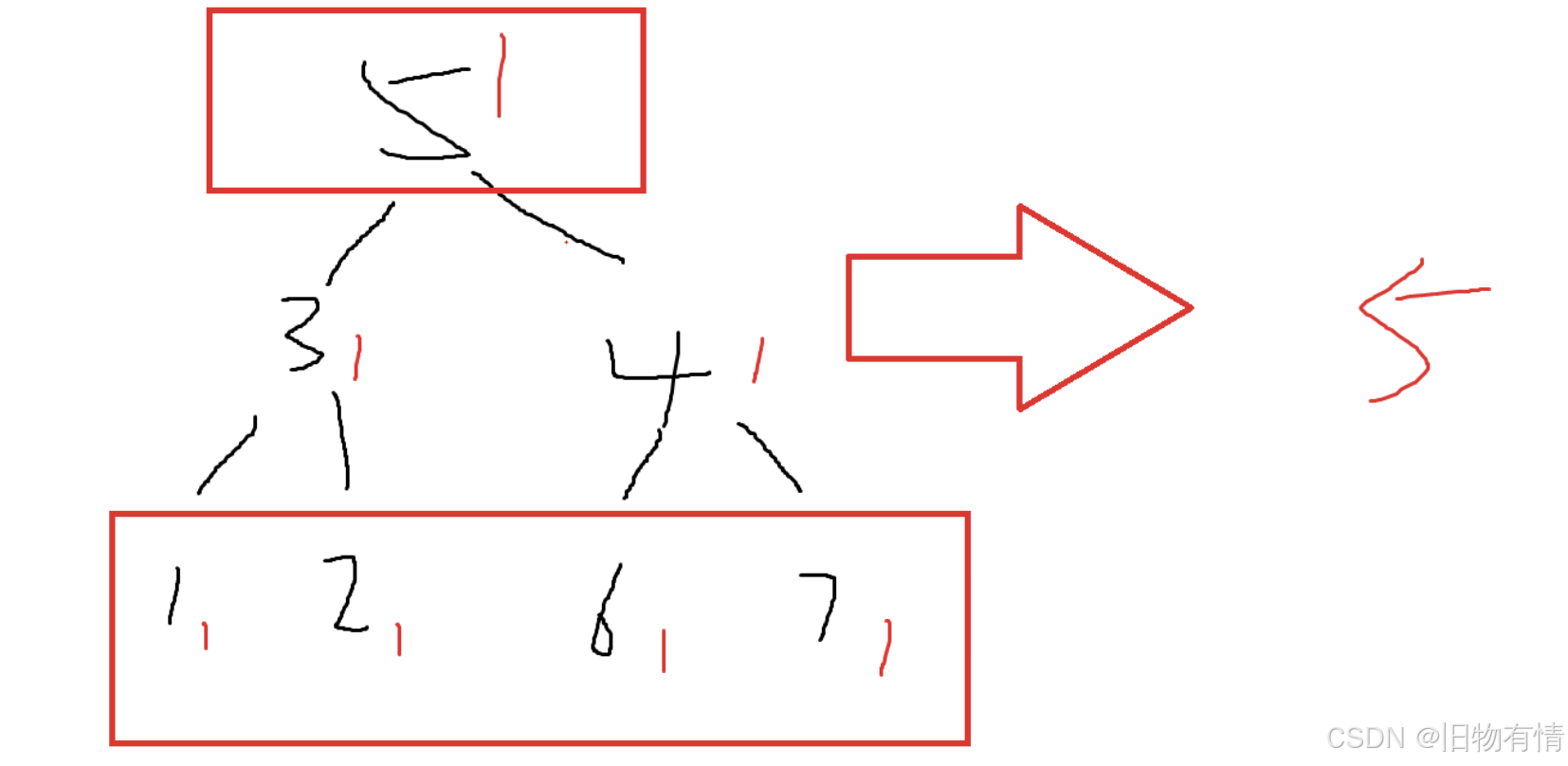
在这里插入图片描述

思路

对于某个根节点来说
如果我们选择当前结点,那么我们就不能选其相邻子节点
反之我们就需要选择相邻子节点

对于本题样例来说，如果选择了5 那么就需要考虑不选择3 和 4的情况
如果不考虑选择 3 和 4 ，对于 3 来说，我们就需要考虑选择 3 的孩子的情况…递归至叶子结点

而答案是从考虑当前结点选择与否推导出来的

状态表示

F[u,0]:所有以u为根的子树中选择,并且不选u这个点的方案

F[u,1]:所有以u为根的子树中选择,并且选u这个点的方案

最后求 max(选,不选)

状态计算

f[u][1] + = f[j][0] j代表其一个孩子节点这里要求累加因为该结点分支节点不一定为1
f[u][0] + = max(f[j][0],f[j][1]) 如果不选,就需要考虑是选了有最大值还是不选有最大值

完整代码

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N =6010;

int n;
int h[N],e[N],ne[N],idx;
int happy[N];//存储开心值
int f[N][2];
bool has_fa[N];//是否有父节点
//树是特殊的图,因此这里用邻接表的形式来存储结点
void add(int a,int b){
	e[idx]=b;
    ne[idx]=h[a];
    h[a]=idx++;
}

void dfs(int u){
    f[u][1]=happy[u];
    
    for(int i=h[u]; i!=-1; i=ne[i]){
        int j=e[i];
        dfs(j);
        f[u][1]+=f[j][0];
        f[u][0]+=max(f[j][0],f[j][1]);
    }
}

int main(){
	cin>>n;
    for(int i=1; i<=n; i++)scanf("%d",&happy[i]);
    
    memset(h,-1,sizeof h);
    
    for(int i=0; i<n-1; i++){
		int a,b;
        scanf("%d%d",&a,&b);
        //b是a的直接上司,b->a
        add(b,a);
        has_fa[a]=true;
    }
    int root=1;
    while(has_fa[root])root++;
    
    dfs(root);
    
    printf("%d\n",max(f[root][0],f[root][1]));
    
    return 0;
}