深度神经网络中的维度问题

1、单一样本时的维度问题

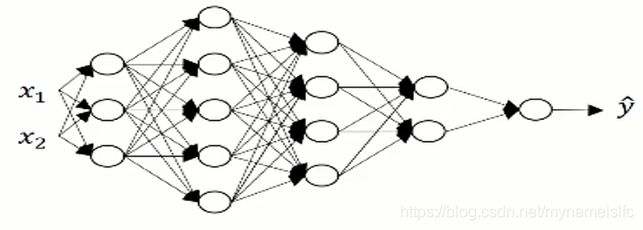
在上图中，$l=5$
正向传播的过程即为：
$z^{[1]}=w^{[1]}x+b^{[1]}$
其中，$z^{[1]}$的维度为（3，1），x即$a^{[0]}$的维度为（2，1），由此可知$w^{[1]}$的维度为（3，2），则$b^{[1]}$的维度为（3，1）。
概括的说，$z^{[1]}$的维度为（$n^{[1]}$，1），x即$a^{[0]}$的维度为（$n^{[0]}$，1），$w^{[1]}$的维度为（$n^{[1]}$，$n^{[0]}$），则$b^{[1]}$的维度为（$n^{[1]}$，1）。（n为每一层中结点个数）
我们以此推论来验证第二层
$z^{[2]}=w^{[2]}{a}^{[1]}+b^{[2]}$
根据推论有，$w^{[2]}$的维度为（$n^{[2]}$，$n^{[1]}$），即（5，3）；$a^{[1]}$与$z^{[1]}$的维度相同，为（3，1），因此，$w^{[2]}\ast a^{[1]}$的维度为（5，1），即为$z^{[2]}$和$b^{[2]}$的维度。
综上，总结如下：
对于单个样本在$l$层的深度神经网络中训练时，
$w^{[l]}$的维度为（$n^{[l]}$，$n^{[l-1]}$）
$b^{[l]}$的维度为（$n^{[l]}$，1）
在反向传播时，$d{w}^{[l]}$和$d{b}^{[l]}$应与$w^{[l]}$和$b^{[l]}$相同
即$d{w}^{[l]}$的维度为（$n^{[l]}$，$n^{[l-1]}$）
$d{b}^{[l]}$的维度为（$n^{[l]}$，1）

2、多样本时的维度问题

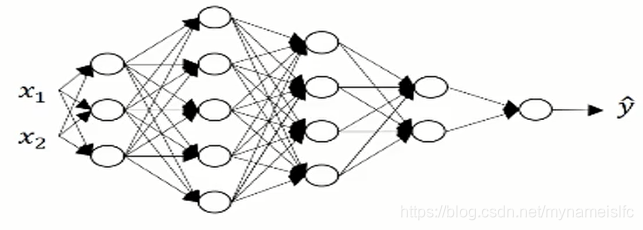
对于单一样本时我们知道：
$z^{[1]}=w^{[1]}x+b^{[1]}$
$z^{[1]}$的维度为（$n^{[1]}$,1）
$w^{[1]}$的维度为（$n^1$,$n^{[0]}$）
$x$的维度为($n^{[0]}$,1)
$b^{[1]}$的维度为（$n^{[1]}$,1）
当样本量为m时：
$z^{[1]}$的维度为（$n^{[1]}$,m）
$w^{[1]}$的维度为（$n^1$,$n^{[0]}$）
$x$即$A^{[0]}$的维度为($n^{[0]}$,m)
$b^{[1]}$的维度还是为（$n^{[1]}$,1），但计算时会采用python对其进行扩展，扩展为（$n^{[1]}$,m）
综上，总结如下：
$z^{[l]},A^{[l]}$的维度为（$n^{[l]}$,m）
反向传播中相同：
$d{z}^{[l]},d{A}^{[l]}$的维度为（$n^{[l]}$,m）