文章目录
一、队列Queue和基本操作
队列和生活中的队一样, F I F O FIFO FIFO,先进先出。
有了实现栈的经验,实现队列就简单了:
void enqueue(E)E dequeue()E getFront()int getSize()boolean isEmpty()
实现一个接口Queue<E>,然后实现一个顺序队列ArrayQueue<E>。
二、动态数组实现顺序队列ArrayQueue
public class ArrayQueue<E> implements Queue<E> {
private Array<E> array;
public ArrayQueue(int capacity) {
array = new Array<>(capacity);
}
public ArrayQueue() {
array = new Array<>();
}
@Override
public int getSize() {
return array.getSize();
}
@Override
public boolean isEmpty() {
return array.isEmpty();
}
@Override
public void enqueue(E e) {
array.addLast(e); //O(1)时间
}
@Override
public E dequeue() {
return array.removeFirst(); //O(N)时间
}
@Override
public E getFront() {
return array.getFirst(); //O(1)时间
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append("Queue: ");
res.append('[');
for (int i = 0; i < array.getSize(); ++i) {
res.append(array.get(i));
if (i != array.getSize() - 1)
res.append(", ");
}
res.append("] tail");
return res.toString();
}
public static void main(String[] args) {
ArrayQueue<Integer> queue = new ArrayQueue<>();
for (int i = 0; i < 10; ++i) {
queue.enqueue(i);
System.out.println(queue);
}
while (queue.getSize() > 2) queue.dequeue();
System.out.println(queue);
}
}
三、数组队列的复杂度分析
void enqueue(E): O ( 1 ) O(1) O(1);均摊;E dequeue(): O ( n ) O(n) O(n);E getFront(): O ( 1 ) O(1) O(1);int getSize(): O ( 1 ) O(1) O(1);boolean isEmpty(): O ( 1 ) O(1) O(1)。
这里我们不难发现,由于我们每次出队的时候都进行了元素的移动,因此出队的复杂度为 O ( n ) O(n) O(n),对于队列来说是不可容忍的。有些顺序队列的实现,不会进行实际的元素移动,因此能够为 O ( 1 ) O(1) O(1),坏处在于有大量冗余的数据浪费空间,好处一是提高了速度,二是存在队列中的冗余数据有时可能会被用到,比如走迷宫的问题。
但是有没有一种方法,既可以提高速度,也可以降低时间复杂度呢?答案就是循环队列!
四、动态数组实现循环队列LoopArray
使用两个指针, f r o n t front front指向队列的开头, t a i l tail tail指向队列结尾的下一个元素,即新元素进队的位置,有 [ f r o n t , t a i l ) [front, tail) [front,tail), f r o n t = = t a i l front == tail front==tail时为空, ( t a i l + 1 ) m o d c a p a c i t y = = f r o n t (tail + 1) \ mod \ capacity == front (tail+1) mod capacity==front时队列满,相当于存在一个空格子没有存储数据。
从个人来看,我倾向于使用 s i z e size size作为队满队空的标记;而且链队列不存在队满的问题,当然,这里通过扩容来避免队满;如果 s i z e = = g e t C a p a c i t y ( ) / 4 size == getCapacity() / 4 size==getCapacity()/4,就缩容到 g e t C a p a c i t y ( ) 2 \frac{getCapacity()}{2} 2getCapacity()的大小。
public class LoopQueue<E> implements Queue<E> {
private E[] data;
private int front, tail;
private int size;
public LoopQueue() {
this(10);
}
public LoopQueue(int capacity) {
data = (E[])new Object[capacity + 1]; //有意思浪费一个元素
front = 0;
tail = 0;
size = 0;
}
public int getCapacity() {
return data.length - 1; //有一个额外的空间被申请
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public int getSize() {
return size;
}
@Override
public void enqueue(E e) {
if ((tail + 1) % data.length == front) //如果循环队列队满
resize(getCapacity() * 2);
data[tail] = e;
tail = (tail + 1) % data.length;
++size;
}
@Override
public E dequeue() {
if (isEmpty())
throw new IllegalArgumentException("Cannot dequeeu from an empty queue.");
E ret = data[front];
data[front] = null;
front = (front + 1) % data.length;
--size;
if (size == getCapacity() / 4 && getCapacity() / 2 != 0) //缩容
resize(getCapacity() / 2);
return ret;
}
@Override
public E getFront() {
if (isEmpty())
throw new IllegalArgumentException("Queue is empty.");
return data[front];
}
private void resize(int newCapacity) {
E[] newData = (E[])new Object[newCapacity + 1];
//把data队列中的元素放到newData的[0,size)区间
for (int i = 0; i < size; ++i) //data有一个front的偏移
newData[i] = data[(i + front) % data.length];
data = newData;
front = 0;
tail = size;
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append(String.format("Queue: size = %d, capacity = %d\n", size, getCapacity()));
res.append("front [");
for (int i = front; i != tail; i = (i + 1) % data.length) {
res.append(data[i]);
if ((i + 1) % data.length != tail)
res.append(", ");
}
res.append(']');
return res.toString();
}
public static void main(String[] args) {
LoopQueue<Integer> queue = new LoopQueue<>();
for (int i = 0; i < 10; ++i) {
queue.enqueue(i);
System.out.println(queue);
}
while (queue.getSize() > 2) queue.dequeue();
System.out.println(queue);
}
}
五、循环队列的复杂度分析
void enqueue(E): O ( 1 ) O(1) O(1);均摊;E dequeue(): O ( 1 ) O(1) O(1);均摊;E getFront(): O ( 1 ) O(1) O(1);int getSize(): O ( 1 ) O(1) O(1);boolean isEmpty(): O ( 1 ) O(1) O(1)。
六、链队的实现
这里的链队的实现不是基于【数据结构Java实现】单链表【最基本的动态数据结构】这篇文章中实现的单链表。
就像使用动态数组实现的顺序队列一样,我们在头部删除元素, O ( n ) O(n) O(n)级别;同样的问题,我们如果仅仅使用单链表来作为队列,在队列尾部加入元素也是 O ( n ) O(n) O(n)级别。
不过,在单链表那篇文章中,我们最后说了有一些小技巧,可以消除这种时间复杂度。
可以存储一个指向链表尾结点的引用,我们加上虚拟头结点,链表头仍然是 O ( 1 ) O(1) O(1)的插入和删除,链表尾是 O ( n ) O(n) O(n)的删除和 O ( 1 ) O(1) O(1)的插入,为此,我们可以将链表尾作为队首,链表头作为队尾,这样实现的队列性能很好;如果不加入虚拟头结点,就需要特判一些情形。
我更倾向于不使用虚拟头结点,在这个情形中,我们在队首不进行添加元素,不用特判;而且仅从队首删除元素,也不需要在删除时特判。需要特判的情形在于, 链表可能为空的时候——head = tail = null。比如enqueue在队尾进行入队,如果此时为空,需要特判,tail = new Node(e); head = tail;。dequeue在队首出队,出队后为空,则要特判,if (head == null) tail = null;
下面实现的队列的操作都是 O ( 1 ) O(1) O(1)的。
public class LinkedQueue<E> implements Queue<E> {
private class Node { //链表结点不变
public E e;
public Node next;
public Node(E e, Node next) {
this.e = e;
this.next = next;
}
public Node(E e) {
this(e, null);
}
public Node() {
this(null, null);
}
@Override
public String toString() {
return e.toString();
}
}
private Node head, tail; //都是引用
private int size;
public LinkedQueue() {
head = null;
tail = null;
size = 0;
}
@Override //获取队列的元素数目
public int getSize() {
return size;
}
@Override //返回队列是否为空
public boolean isEmpty() {
return size == 0;
}
@Override
public void enqueue(E e) {
if (tail == null) { //空链表进元素, 特判
tail = new Node(e);
head = tail;
} else {
tail.next = new Node(e);
tail = tail.next;
}
++size;
}
@Override
public E dequeue() {
if (isEmpty())
throw new IllegalArgumentException("Cannot dequeue from an empty queue.");
Node retNode = head;
head = head.next;
if (head == null) //如果出队后为空链表
tail = null;
retNode.next = null; //从链表中断开原来的头结点
--size;
return retNode.e;
}
@Override
public E getFront() {
if (isEmpty())
throw new IllegalArgumentException("Cannot dequeue from an empty queue.");
return head.e;
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append("Queue: front ");
Node cur = head;
while (cur != null) {
res.append(cur.e + "->");
cur = cur.next;
}
res.append("NULL tail");
return res.toString();
}
public static void main(String[] args) {
LinkedQueue<Integer> queue = new LinkedQueue<>();
for (int i = 0; i < 10; ++i) {
queue.enqueue(i);
System.out.println(queue);
}
while (queue.getSize() > 2) queue.dequeue();
System.out.println(queue);
}
}
七、三个队列的性能比较
用一个测试实际运行时间的类,来比较一下两者的性能:
对数组队列和循环队列,分别运行10万次入队和出队。
import java.util.Random;
public class Test {
private static double testQueue(Queue<Integer> q, int opCount) {
long startTime = System.nanoTime(); //纳秒
Random random = new Random();
for (int i = 0; i < opCount; ++i)
q.enqueue(random.nextInt(Integer.MAX_VALUE)); //[0, bound)的一个随机数
for (int i = 0; i < opCount; ++i)
q.dequeue();
long endTime = System.nanoTime();
return (endTime - startTime) / 1000000000.0;
}
public static void main(String[] args) {
int opCount = 10_0000;
ArrayQueue<Integer> arrayQueue = new ArrayQueue<>();
double time1 = testQueue(arrayQueue, opCount);
System.out.println("ArrayQueue, time: " + time1 + "s.");
LoopQueue<Integer> loopQueue = new LoopQueue<>();
double time2 = testQueue(loopQueue, opCount);
System.out.println("LoopQueue, time: " + time2 + "s.");
LinkedQueue<Integer> linkedQueue = new LinkedQueue<>();
double time3 = testQueue(linkedQueue, opCount);
System.out.println("LinkedQueue, time: " + time3 + "s.");
}
}
结果如图:
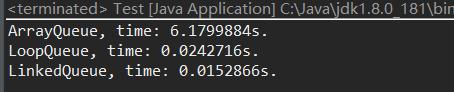
数组队列和循环队列有300倍的性能差距,差在出队操作上,数组队列出队
O
(
n
)
O(n)
O(n),循环队列出队为
O
(
1
)
O(1)
O(1)。链表队列再这次测试中表现最好。










 本文深入探讨了队列数据结构的实现与优化,包括顺序队列、循环队列及链队列的不同特性与应用场景,对比分析了它们的时间复杂度与性能表现。
本文深入探讨了队列数据结构的实现与优化,包括顺序队列、循环队列及链队列的不同特性与应用场景,对比分析了它们的时间复杂度与性能表现。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










