简单介绍一下对非线性最小二乘问题的数学理解,有不足之处还望批评指正~
一、最小二乘问题定义
No1.最小二乘问题定义:
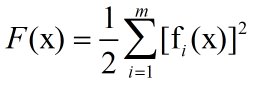
找到一个![]() 使得F(x)值最小,即使残差平方和最小。(式中1/2作为常数对问题本质没有影响,有的地方也没有这个1/2)。
使得F(x)值最小,即使残差平方和最小。(式中1/2作为常数对问题本质没有影响,有的地方也没有这个1/2)。
对于F(x)最小,则又分为局部最小No2和全局最小No3
No2.局部最小
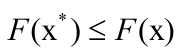 for
for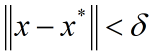
即在一个固定领域内,![]() 使得
使得![]() 最小。
最小。
No3.全局最小
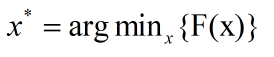
即![]() 使得
使得![]() 在整个函数定义域最小。
在整个函数定义域最小。
对代价函数F(x)进行泰勒展开并只保留二阶量

J为雅克比矩阵,H为海塞矩阵。
我们的目的(也是最小二乘的目的)就是找到一个x,使得代价函数F(x)最小,即残差平方和最小。因此,我们可以通过迭代的方式,让每次迭代的结果 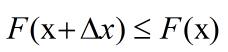 ,使得代价函数不断减小。
,使得代价函数不断减小。
很明显F(x)在导数为0时,有稳定点(极大值点、极小值点和鞍点),我们要求的相当于是极小值点,又当![]() 在
在![]() 处为稳定点时,若H矩阵为正定的,则此时为极小值点。
处为稳定点时,若H矩阵为正定的,则此时为极小值点。
即代入![]() (求的未知量是
(求的未知量是![]() ,故对其求导),可得
,故对其求导),可得![]() 即
即![]() 。又因为前面保证了H的正定性,所以H是可逆的。这就是牛顿法。
。又因为前面保证了H的正定性,所以H是可逆的。这就是牛顿法。
二、写的有点烦...不想写了orz




 本文深入探讨非线性最小二乘问题,解析其数学原理,包括局部与全局最小值概念,通过泰勒展开简化问题,并介绍如何利用牛顿法迭代求解,以达到残差平方和最小化。
本文深入探讨非线性最小二乘问题,解析其数学原理,包括局部与全局最小值概念,通过泰勒展开简化问题,并介绍如何利用牛顿法迭代求解,以达到残差平方和最小化。

















 751
751

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










