Slam 14讲学习笔记 —— 第五讲 —— 相机与图像

本讲主要搞清楚相机的针孔模型、透镜的畸变模型。从而弄清成像（外部的三维点投影到相机内部成像平面）及相机的内外参。

一. 相机模型：针孔（小孔）成像模型：

上图的几何模型如下：
O—x—y—z为相机坐标系（z指向相机的前方，x指向相机的右方，y指向下，O为相机的光心）。成像平面O’—x’—y’，现实世界的P点经过相机光心（小孔）投影后在成像平面上为像点P’。
设P点坐标为[X,Y,Z]，P’坐标为[X’,Y’,Z’]，并设焦距(光心到成像平面的距离）为f，则有：
负号表示成像为倒的，为了简化模型，可以把成像平面对称到相机前方：

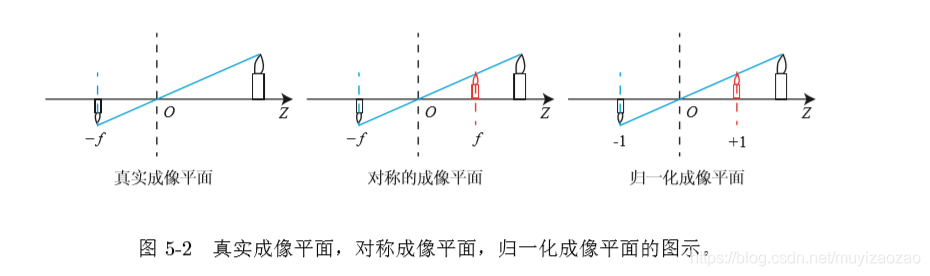
所以上式变为：

整理后：

上式描述了物理空间点P和它的像点P’的空间关系。

但是我们在相机中获得的是一个个的像素，需要在成像平面对像进行采样和量化。为了将相机上感受的光线转化为图像像素，设在成像平面（原点对称到相机前方）上有一像素平面o-u-v。在像素平面得到P’的坐标为（u,v)。

直接得出“P点的像”在像素平面的像素坐标(u,v)和空间点P在相机坐标下的坐标（X,Y,Z)的关系：