Reconstruction
已知两幅图中的匹配点
{xi,xi′}
\left\{\boldsymbol{x}_{i}, \boldsymbol{x}_{i}^{\prime}\right\}
{xi,xi′}
估计camera matrix
P,P′
\mathbf{P}, \mathbf{P}^{\prime}
P,P′
和3D点.
X
X
X
1 第一步计算基础矩阵F
x′TFx=0
\boldsymbol{x'}^{T} \mathbf{F} \boldsymbol{x}=0
x′TFx=0
2 设第一个相机对应的camera matrix 为
P=[I∣0]=[100001000010]
\mathbf{P}=[\mathbf{I} | \mathbf{0}]=
\left[\begin{array}{llll}
{1} & {0} & {0} & {0} \\
{0} & {1} & {0} & {0} \\
{0} & {0} & {1} & {0}
\end{array}\right]
P=[I∣0]=⎣⎡100010001000⎦⎤
世界坐标系和相机坐标系统一.
第二个相机对应的camera matrix为
P′=K[100001000010][Rt0T1]
\mathbf{P'}=\mathbf{K}\left[\begin{array}{llll}
{1} & {0} & {0} & {0} \\
{0} & {1} & {0} & {0} \\
{0} & {0} & {1} & {0}
\end{array}\right]\left[\begin{array}{ll}
{\mathbf{R}} & {\mathbf{t}} \\
{\mathbf{0}^{\mathrm{T}}} & {1}
\end{array}\right]
P′=K⎣⎡100010001000⎦⎤[R0Tt1]
由于基础矩阵F是点在图像坐标系下的转化矩阵,而本质矩阵F是点在摄像机坐标系下的转化,因此,在这里我们需要得到本质矩阵E.
为什么?
因为我们得到图像坐标系下的点x是从世界坐标系到相机坐标系再到图像坐标系.
所以我们要求世界坐标系下的点X就需要从像素坐标系(求F)到图像坐标系(求E)再到世界坐标系(得到X).
所以现在求得F,就需要从F推出E.
公式如下:
E=K′⊤FK
\mathbf{E}=\mathbf{K}^{\prime \top} \mathbf{F} \mathbf{K}
E=K′⊤FK
E是由6个外参组成的.
E=[R∣T]
\mathbf{E}=[\mathbf{R} | \mathbf{T}]
E=[R∣T]
现在如何分解E求得R和T呢?
用SVD
E=UΣV⊤
\mathbf{E}=\mathbf{U} \boldsymbol{\Sigma} \mathbf{V}^{\top}
E=UΣV⊤
之前有说过,这样分解出来秩不一定等于2,所以需要调整.
令W=[0−10100001]
\mathbf{W}=\left[\begin{array}{ccc}
{0} & {-1} & {0} \\
{1} & {0} & {0} \\
{0} & {0} & {1}
\end{array}\right]
W=⎣⎡010−100001⎦⎤
还有就是U和V的行列式都必须要大于0,如果不大于0,需要乘-1让其大于0.
这里我也不知道原因.
det(U)>0∧det(V)>0
\operatorname{det}(U)>0 \wedge \operatorname{det}(V)>0
det(U)>0∧det(V)>0
不过我之前有看过说也可以判断R的行列式是不是等于1的.因为R的行列式等于-1意味着旋转和反射? 不是很懂. 求解.
总之这样弄下来,我们可以得到两个R,两个T.
R1=UWV⊤R2=UW⊤V⊤T1=U3T2=−U3
\mathbf{R}_{1}=\mathbf{U} \mathbf{W} \mathbf{V}^{\top} \quad \mathbf{R}_{2}=\mathbf{U} \mathbf{W}^{\top} \mathbf{V}^{\top} \quad \mathbf{T}_{1}=U_{3} \quad \mathbf{T}_{2}=-U_{3}
R1=UWV⊤R2=UW⊤V⊤T1=U3T2=−U3
所以到底该选择哪个R和T组成H(外参对应的矩阵)呢?
H=[Rt0T1]
H=\left[\begin{array}{cc}
{\mathbf{R}} & {\mathbf{t}} \\
{\mathbf{0}^{\mathrm{T}}} & {1}
\end{array}\right]
H=[R0Tt1]
3.根据前面写的P’的公式,求出这四组E和R对应的P’,再用triangularization恢复出X在相机世界坐标系下的点(见triangularization相关文章).
选择Z>0的点,这样就一定在两个相机镜头的前面.
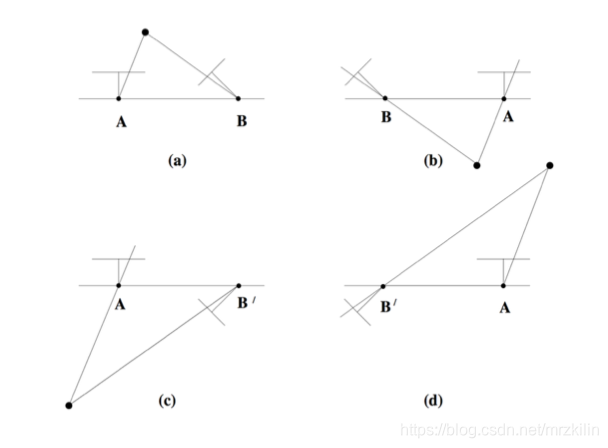
只有(a)是符合点X在两个摄像机前方的.
因为是以第一个相机为参考坐标系,所以第一个相机的坐标是(0,0,0,1)
从图上可以看出,B到A的三个平移变量,Z是肯定不变的,所以第二个相机的Z也是0.
总之这样判断就可以求出P啦.





 本文详细介绍了从两幅图像中提取的匹配点出发,通过计算基础矩阵F,进而推导出本质矩阵E,利用SVD分解获取旋转矩阵R和平移向量T的过程,最终实现三维点的恢复。文中还探讨了如何选择正确的R和T,以及如何判断点在两个相机前的条件。
本文详细介绍了从两幅图像中提取的匹配点出发,通过计算基础矩阵F,进而推导出本质矩阵E,利用SVD分解获取旋转矩阵R和平移向量T的过程,最终实现三维点的恢复。文中还探讨了如何选择正确的R和T,以及如何判断点在两个相机前的条件。

















 1815
1815

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








