简单的动态规划

动态规划精讲

最新推荐文章于 2024-10-08 10:18:36 发布

原创最新推荐文章于 2024-10-08 10:18:36 发布 · 1w 阅读

1 ·

CC 4.0 BY-SA版权

算法专栏收录该内容

1 篇文章

订阅专栏

认识动态规划

以下是一段描述斐波那契数列的简单代码。本质是一个递归的方案，它的计算过程是不断的将大计算拆分成小计算，最后再对小计算的结果进行合并。然而递归方案的时间复杂度非常高，为O(2^n)。当n非常大的时候会产生高昂的时间成本。

  /**
   * 经典的fabonacci问题，1 1 2 3 5 8 13 21...
   * 使用递归算法实现，本质是一种分治策略，自顶向下。
   * 不断的将大计算拆分成小计算，最后再对小计算的结果进行合并。
   * 递归的缺点是不能复用小计算的结果，导致时间复杂度非常高，本方案时间复杂度O(2^n)，空间复杂度O(1)
   * @param n
   * @return
   */
  private static int fabonacci(int n) {
    if (n==0) {
      return 1;
    }
    if (n==1) {
      return 1;
    }
    return fabonacci(n-1)+fabonacci(n-2);
  }

那么，这段代码有什么优化方案吗。试想，如果我们从第三个数开始，每次计算都能够把当前的斐波那契数存起来给下一个数字计算使用，那么不就避免了递归了吗？

  /**
   * 使用动态规划优化fabonacci。
   * 不同于递归算法，动态规划的核心是能够复用上次计算的结果。
   * 本题采用动态规范，建立一个数组保存每个fabonacci数列的值，返回某个数列的值通过数组下标直接返回即可。
   * 时间复杂度O(n),空间复杂度O(n)
   * @param n
   * @return
   */
  private static int fabonacci2(int n) {
    if (n==0) {
      return 1;
    }
    if (n==1) {
      return 1;
    }
    int[] res = new int[n+1]; //存储每个可能
    res[0] = 1;
    res[1] = 1;
    for (int i = 2; i < n+1; i++) {
      res[i] = res[i-1]+res[i-2];
    }
    return res[n];
  }

上面这段代码通过一个数组存储每次计算出的斐波那契数值，当需要下一个数值时，直接从数组中取出前两个数作为求和基数，这就是一个简单的动态规划方案。

动态规划的核心是能够复用上次计算的结果，它能够把一个大问题拆成一堆可以“递进式”解决的小问题，这样可以从小问题开始解决，并存储小问题的解，在解决更大的小问题时，可以复用前面小问题的解。

状态转移方程

动态规划问题都会涉及一个名词，状态转移方程，这也是解决动态规划问题的核心。对于上面的斐波那契数列来说，状态转移方程就是

f(n) = f(n-1) + f(n-2)

台阶问题

一个人爬楼梯，每次只能爬1个或2个台阶，假设有n个台阶，那么这个人有多少种不同的爬楼梯方法？
换个角度思考：
1）第1步走1个台阶，剩余n-1个台阶有多少种走法？
2）第2步走2个台阶，剩余n-2个台阶有多少种走法？
所以n个台阶的走法，即为先走1个台阶后剩余台阶的走法数量加上先走2个台阶后剩余台阶的走法数量。容易推导出这本质上也是个斐波那契数列。即状态转移方程：

f(n) = f(n-1) + f(n-2)

兔子跳台阶问题

刚刚那个人爬楼梯问题，如果我们衍生一下：
一只兔子，每次只能爬1个，3个台阶，假设有n个台阶，那么这只兔子有多少种走法？
同样的思考角度：
1）第一步跳1个台阶，剩余n-1个台阶多少种的跳法？
2）第一步跳3个台阶，剩余n-3个台阶多少种的跳法？
同理，可以推导出动态规范的状态转移方程：

f(n) = f(n-1) + f(n-3)

这个问题就是斐波那契数列的衍生，不同点在于求和基数的间隔。

/**
 * 一只兔子，每次只能跳1个或者3个台阶，假设有n个台阶，那么这只兔子到达最上层台阶共有多少种跳法？
 * 典型的动态规划问题：
 * 假设台阶数设为n，走法数量为k：
 * n = 1	k = 1（1）
 * n = 2	k = 1（1+1）
 * n = 3	k = 2（1+1+1，3）
 * n = 4	k = 3（1+1+1+1，1+3，3+1）
 * n = 5	k = 4（1+1+1+1+1，1+1+3，1+3+1，3+1+1）
 *
 * 显然，根据第一步跳法不同，可以总结出规律：
 * 第一步跳1阶，剩下n-1阶的跳法为m，第二步跳3阶，剩下n-3阶的跳法为n。m+n即为n个台阶的总跳法数。
 * 以上括号中也说明了确实是m+n这个关系！
 * 即: f(n) = f(n-1)+f(n-3)
 *
 */
  private static int stage(int n) {
    int[] res =  new int[n];
    res[0] = 1;
    res[1] = 1;
    res[2] = 2;
    for (int i = 3; i < n; i++) {
      res[i] = res[i-1] + res[i-3];
    }
    return res[n-1];
  }

硬币找零问题

假设有1元，5元，11元这三种面值的硬币，给定一个整数金额，比如15元，最少使用的硬币组合数是什么？
设金额为s，最少硬币组合数为n，我们先通过枚举来看看这两个数之间的关系，括号里面展示具体的组合方案。

s = 1	n = 1	(1)
s = 2	n = 2	(1+1)
s = 3	n = 3	(1+1+1)
s = 4 	n = 4	(1+1+1+1)
s = 5 	n = 1	(5, 1+1+1+1+1+1)
s = 6	n = 2	(5+1, 1+1+1+1+1+1+1)
s = 7	n = 3	(5+1+1, 1+1+1+1+1+1+1+1)	
s = 8	n = 4	(5+1+1+1, 1+1+1+1+1+1+1+1+1)
s = 9	n = 5	(5+1+1+1+1, 1+1+1+1+1+1+1+1+1+1)
s = 10	n = 2	(5+5, 5+1+1+1+1+1, 1+1+1+1+1+1+1+1+1+1+1)
s = 11	n = 1	(11)

我们通过一个建立一个长度为3的数组，分别存储使用面值为1，5，11元所需要的硬币数量，对上面的分析进行抽象：

s = 1	n = 1(1)			[1,0,0]
s = 2	n = 2(1+1)		  	[2,0,0]
s = 3	n = 3(1+1+1)		[3,0,0]
s = 4 	n = 4(1+1+1+1)	    [4,0,0]
s = 5 	n = 1(5)		  	[0,1,0]
s = 6	n = 2(5+1）		    [1,1,0]
s = 7	n = 3(5+1+1)	    [2,1,0]
s = 8	n = 4(5+1+1+1)	    [3,1,0]
s = 9	n = 5(5+1+1+1+1)    [4,1,0]
s = 10	n = 2(5+5)		    [0,2,0]
s = 11  n = 1				[1,0,0]

思考：
1）当金额数为1，由于小于等于当前金额的最大面值是1，所以最少组合数为1
2）当金额数为2，由于小于等于当前金额的最大面值是1，所以最少组合数为1）的组合数+1，即2
3）当金额数为3，由于小于等于当前金额的最大面值是1，所以最少组合数为1）的组合数+2，即3
…
5）当金额数为5，由于小于等于当前金额的最大面值是5，所以最少组合数为1
6）当金额数为6，由于小于等于当前金额的最大面值是5，所以最少组合数为5）的组合数+1，即2
7）当金额数为7，由于小于等于当前金额的最大面值是5，所以最少组合数为5）的组合数+2，即3
…
10）当金额数为10，由于小于等于当前金额的最大面值是5，所以最少组合数为2
11）当金额数为11，由于小于等于当前金额的最大面值是11，所以最少组合数为1
12）当金额数为12，由于小于等于当前金额的最大面值是11，所以最少组合数为11）的组合数+1，即2

可以总结出状态转移方程：

dp[i] = min{dp(i-1), dp(i-5), dp(i-11)}+1

实现这个算法的代码

/**
 * 假设有1元，5元，11元这三种面值的硬币，给定一个整数金额，比如15元，最少使用的硬币组合是什么？
 * 思考：设金额为s，硬币数为n，则
 * s = 1	n = 1(1)			[1,0,0]
 * s = 2	n = 2(1+1)		  	[2,0,0]
 * s = 3	n = 3(1+1+1)		[3,0,0]
 * s = 4 	n = 4(1+1+1+1)	    [4,0,0]
 * s = 5 	n = 1(5)		  	[0,1,0]
 * s = 6	n = 2(5+1）		    [1,1,0]
 * s = 7	n = 3(5+1+1)	    [2,1,0]
 * s = 8	n = 4(5+1+1+1)	    [3,1,0]
 * s = 9	n = 5(5+1+1+1+1)    [4,1,0]
 * s = 10	n = 2(5+5)		    [0,2,0]
 * s = 11   n = 1				[1,0,0]
 *
 */
private static int leastCoin(int[] coin, int money) {
  int[] minCoins = new int[money+1];
  if (money <= 0) {
    return 0;
  }
  for (int sum = 1; sum <= money; sum++) {
    int min = sum; // 使用最小面额，需要的硬币数量是最多的，也就是当前的金额总额
    for (int kind = 0; kind < coin.length; kind++) {
      int kindValue = coin[kind]; ////逐渐扩大面额，当面额逐渐扩大，需要的张数越来越少
      if (kindValue <= sum) {
        //eg；sum=3，即3元比2元多了1元，2元为2种组合，3元的组合为2元组合+1 ...
        //eg；sum=4，即4元比3元多了1元，3元为3种组合，4元的组合为3元组合+1 ...
        //eg；sum=5，即5元比1元多了4元，4元为4种组合，5元的组合为4元组合+1，所以是5种; 但当kindValue=5时，5元比5元多了0元，0元的组合+1为1
        //eg；sum=6，即6元比5元多了1元，1元为1种组合，6元为1元组合+1 ...
        //eg；sum=7，即7元比5元多了2元，2元为2种组合，7元为2元组合+1 ...
        int temp = minCoins[sum - kindValue] + 1;
        if (temp < min) {
          min = temp;
        }
      }
      minCoins[sum] = min;
    }
  }
  return minCoins[money];
}

求三角形最短路径和

如图一个三角形由一串数字组成，要求从顶点2开始走到最低下边的最短路径和，要求只能向下边左右两个结点走，如3可以走向6，5，但不能走到7，5能走到1，8，但不能走到3或4。图中的最短路径和应该为2+3+5+1=11。设计算法计算出最短路径和。
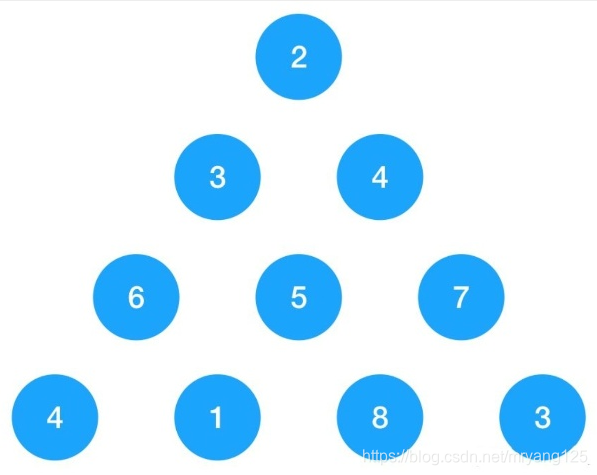
在这里插入图片描述
首先用一个二维数组表示整个三角形，缺失的结点用0表示。

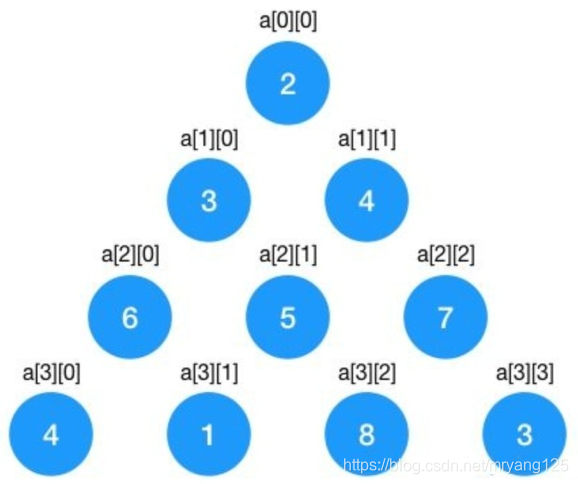
我们的数组应该定义如下：

private static int[][] triangle = {
    {2, 0, 0, 0},
    {3, 4, 0, 0},
    {6, 5, 7, 0},
    {4, 1, 8, 3}
};

思考：
如果计算2到底部的最短路径和，只需要计算3，4 到最底部的最短路径之和，然后取二者最小值加上2即可。
同理要计算3，4到最底部的路径最小值，只需要计算它们的左右结点到底部最短路径最小值加上本身即可。
从顶向下，本质还是个递归的思想。

采用动态规划：
三角形的最后一层节点，它们到底部的最短路径就是其本身，于是问题转化为了已知最后一层节点的最小值怎么求倒数第二层到最开始的节点到底部的最小值了。先看倒数第二层到底部的最短路径怎么求：
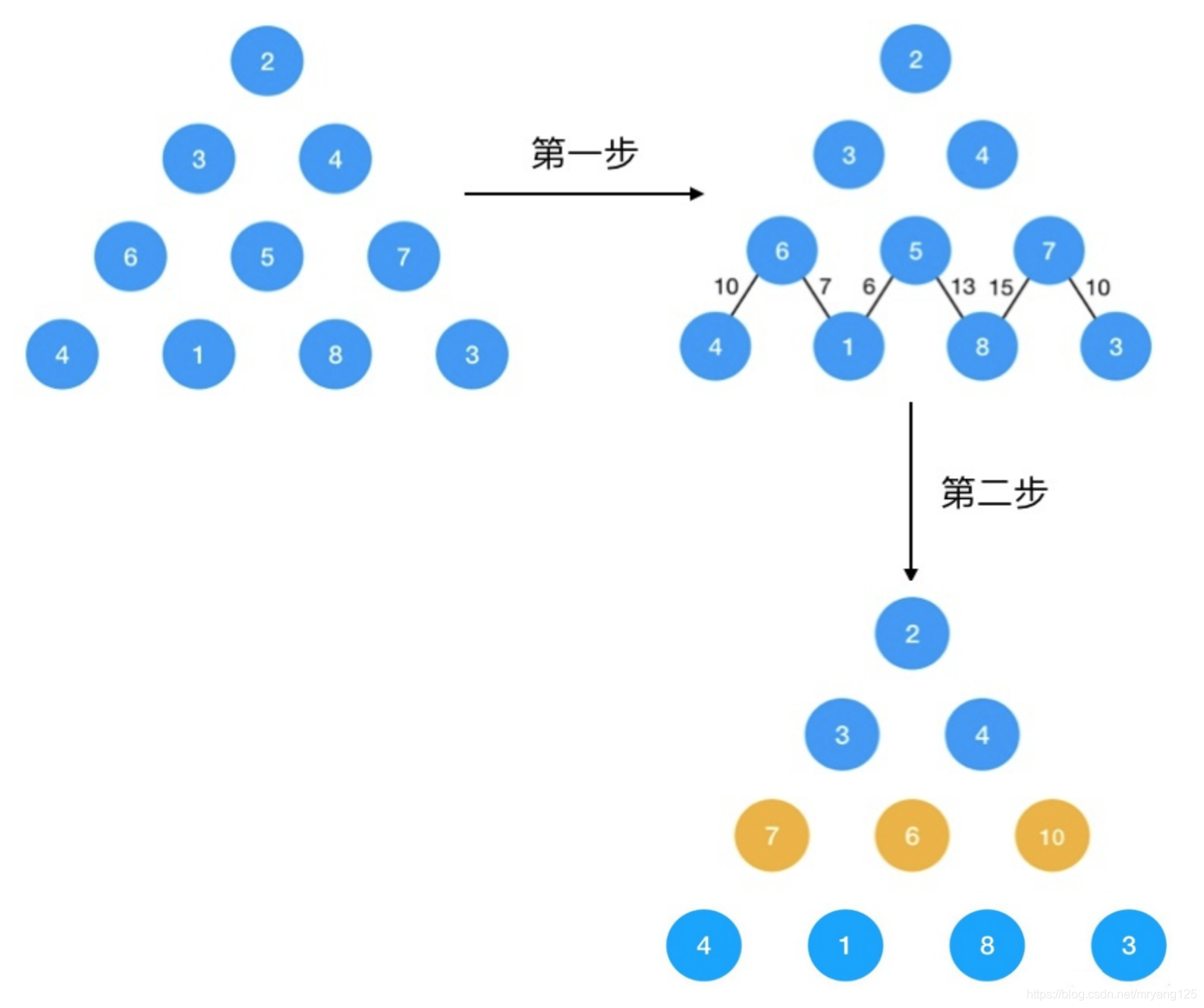
在这里插入图片描述
同理，第二层对于节点 3 ，它到最底层的最短路径转化为了 3 到 7， 6 节点的最短路径的最小值，即 9, 对于节点 4，它到最底层的最短路径转化为了 4 到 6， 10 的最短路径两者的最小值，即 10。

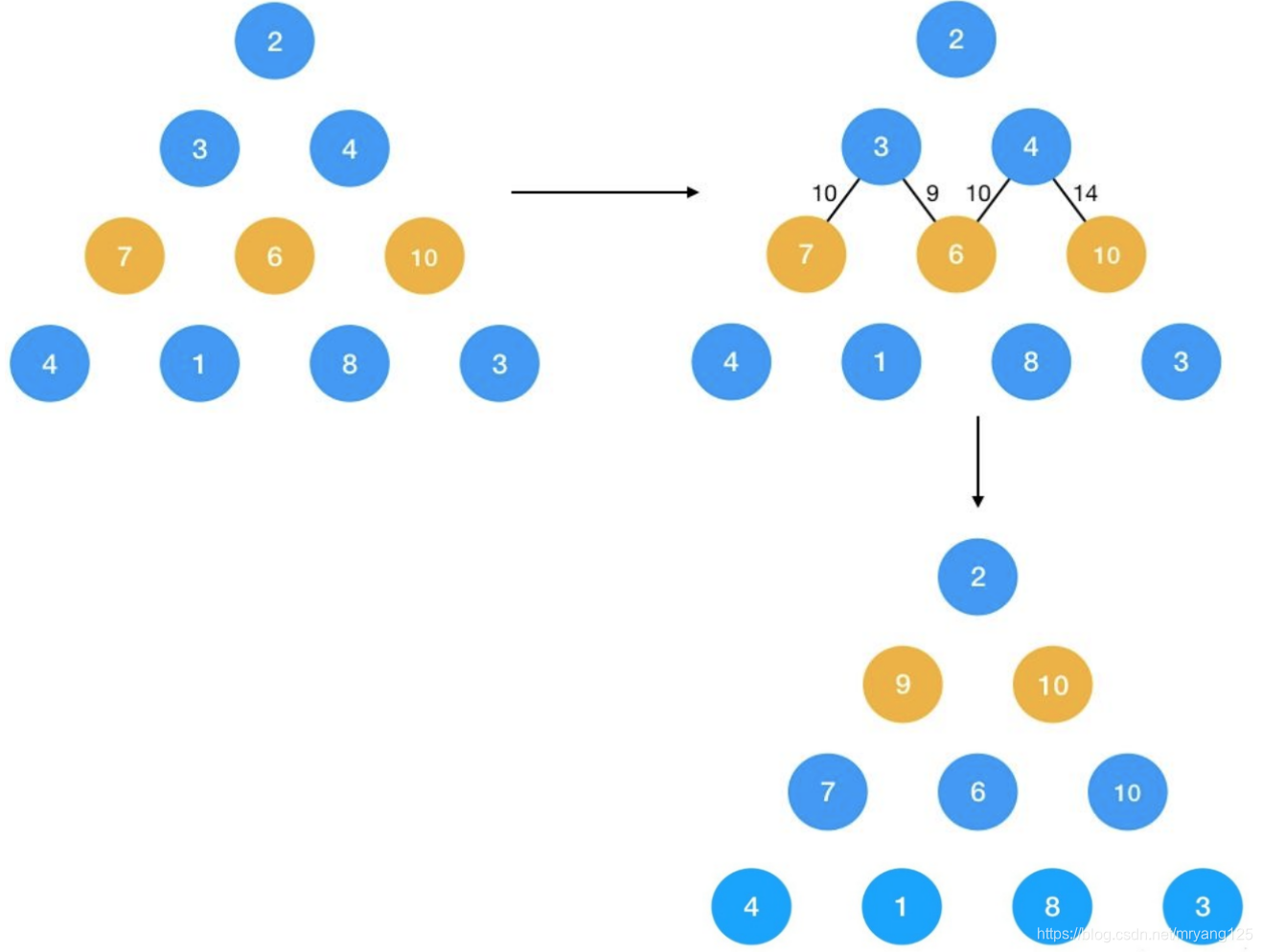
接下来要求 2 到底部的路径就很简单了，只要求 2 到节点 9 与 10 的最短路径即可，显然为 11。
根据这个过程，定义dp[i][j]为(i,j)到最底部最短路径之和，我们可以推导出动态规划的状态转移方程：

dp[i][j] = triangle[i][j] + Math.min(dp[i+1][j], dp[i+1][j+1]);

有了状态转移方程，代码就很好实现了，以下是利用动态规划实现的求解最短路径之和的算法。空间复杂度O(1)，时间复杂度O(n^2)，代码如下：

private static int traverse() {
  for (int i = 2; i >= 0 ; i--) { //只需要从倒数第二层开始，因为最底层本身可看作是个路径
    for (int j = 0; j < 3; j++) { //因为三角形当前层的节点数会比下面一层结点数多1，所以注意不能溢出即可。
      triangle[i][j] = triangle[i][j] + Math.min(triangle[i+1][j], triangle[i+1][j+1]);
    }
  }
  return triangle[0][0];
}

当然这个算法缺点是直接改变了原始的三角形，可新建一个额外的三角形来避免:

private static int traverse() {
  int m = triangle.length-2;
  int n = triangle[0].length-1;
  for (int i = m; i >= 0 ; i--) {
    for (int j = 0; j < n; j++) {
      triangle[i][j] = triangle[i][j] + Math.min(triangle[i+1][j], triangle[i+1][j+1]);
    }
  }
  return triangle[0][0];
}