机器学习算法必掌握的 12 种概率分布（附 Python 代码实现）

机器学习开发者需要了解的 12 种概率分布，这些你都了解吗？
机器学习有其独特的数学基础，我们用微积分来处理变化无限小的函数，并计算它们的变化；我们使用线性代数来处理计算过程；我们还用概率论与统计学建模不确定性。在这其中，概率论有其独特的地位，模型的预测结果、学习过程、学习目标都可以通过概率的角度来理解。

与此同时，从更细的角度来说，随机变量的概率分布也是我们必须理解的内容。在这篇文章中，项目作者介绍了所有你需要了解的统计分布，他还提供了每一种分布的实现代码。

项目地址：https://github.com/graykode/distribution-is-all-you-need

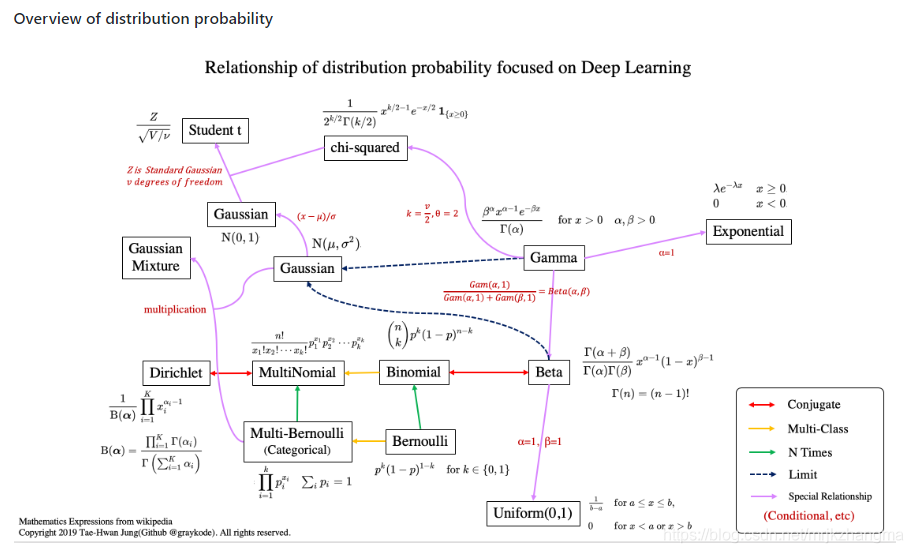
概率分布与特性

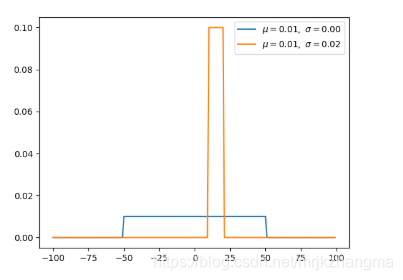
1.均匀分布（连续型）

均匀分布是指闭区间 [a, b] 内的随机变量，且每一个变量出现的概率是相同的。 代码实现

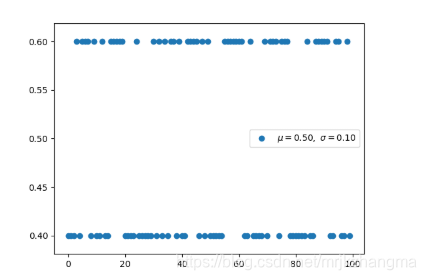
2. 伯努利分布（离散型）

• 伯努利分布并不考虑先验概率 P(X)，它是单个二值随机变量的分布。它由单个参数φ∈ [0, 1] 控制，φ 给出了随机变量等于 1 的概率。
• 我们使用二元交叉熵函数实现二元分类，它的形式与对伯努利分布取负对数是一致的。
• 代码实现

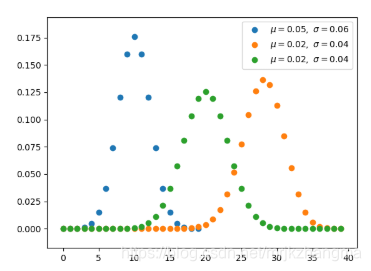
3. 二项分布（离散型）

• 二项分布是由伯努利提出的概念，指的是重复 n 次独立的伯努利试验。
• 在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立。
• 代码实现
  

4.Multi-Bernoulli 分布（离散型）

• Multi-Bernoulli 分布又称为范畴分布（Categorical distribution），它的类别超过 2.
• 交叉熵的形式与该分布的负对数形式是一致的。
• 代码实现

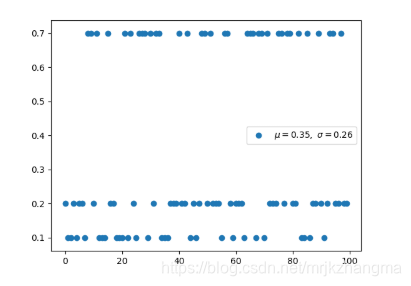
5. 多项式分布（离散型）

• 范畴分布是多项式分布（Multinomial distribution）的一个特例，它与范畴分布的关系就像伯努利分布与二项分布之间的关系。
• 代码实现

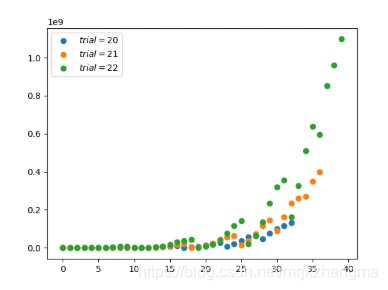
6.Beta 分布（连续型）

• 贝塔分布（Beta Distribution) 是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数，它指一组定义在 (0,1) 区间的连续概率分布。
• 均匀分布是 Beta 分布的一个特例，即在 alpha=1、 beta=1 的分布。
• 代码实现
  

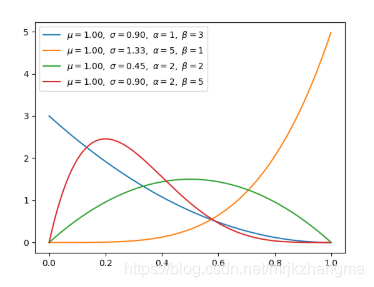
7. 狄利克雷分布（连续型）

• 狄利克雷分布（Dirichlet distribution）是一类在实数域以正单纯形（standard simplex）为支撑集（support）的高维连续概率分布，是 Beta 分布在高维情形的推广。在贝叶斯推断中，狄利克雷分布作为多项式分布的共轭先验得到应用，在机器学习中被用于构建狄利克雷混合模型。
• 代码实现

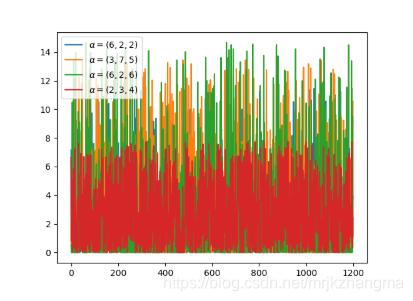
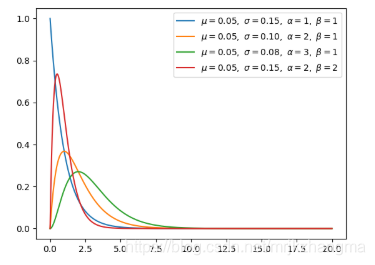
8.Gamma 分布（连续型）

• Gamma 分布是统计学中的常见连续型分布，指数分布、卡方分布和 Erlang 分布都是它的特例。如果 Gamma(a,1) / Gamma(a,1) + Gamma(b,1)，那么 Gamma 分布就等价于 Beta(a, b) 分布。
• 代码实现

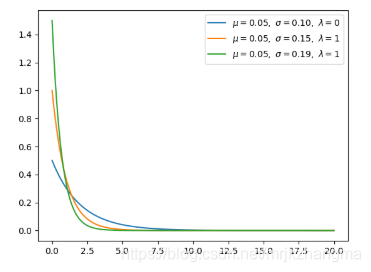
9. 指数分布（连续型）

• 指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进入机场的时间间隔、打进客服中心电话的时间间隔等等。当 alpha 等于 1 时，指数分布就是 Gamma 分布的特例。
• 代码实现

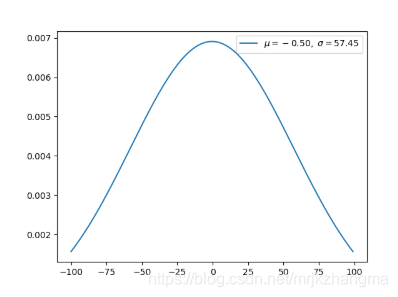
10. 高斯分布（连续型）

• 高斯分布或正态分布是最为重要的分布之一，它广泛应用于整个机器学习的模型中。例如，我们的权重用高斯分布初始化、我们的隐藏向量用高斯分布进行归一化等等。
• 代码实现

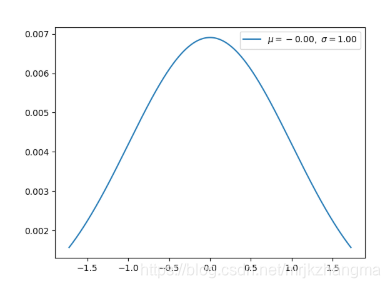
标准正态分布： 均值为0，方差为1
代码实现

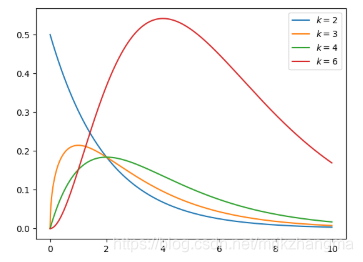
11. 卡方分布（连续型）

• 简单而言，卡方分布（Chi-squared）可以理解为，k 个独立的标准正态分布变量的平方和服从自由度为 k 的卡方分布。卡方分布是一种特殊的伽玛分布，是统计推断中应用最为广泛的概率分布之一，例如假设检验和置信区间的计算。
• 代码实现

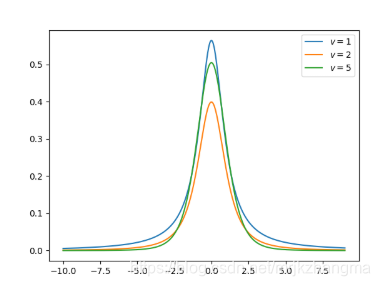
12. 学生 t-分布

• 学生 t-分布（Student t-distribution）用于根据小样本来估计呈正态分布且变异数未知的总体，其平均值是多少。t 分布也是对称的倒钟型分布，就如同正态分布一样，但它的长尾占比更多，这意味着 t 分布更容易产生远离均值的样本。
• 代码实现
  

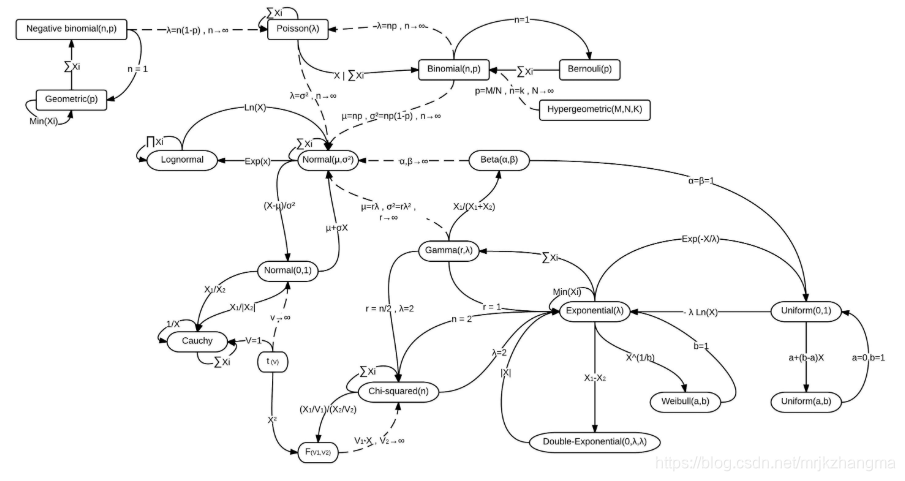
各大分布之间的联系