大白话DC3算法

原创 已于 2024-05-20 08:58:15 修改 · 1.9k 阅读 · 33 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法 #Java #DC3

于 2024-05-19 23:03:25 首次发布

DC3算法是什么

DC3算法（也称为Skew算法）是一种高效的构建后缀数组的算法，全称为Difference Cover Modulo 3算法。

该算法于2002年被提出，论文参考：

https://www.cs.cmu.edu/~guyb/paralg/papers/KarkkainenSanders03.pdf

后缀树的引入

后缀数组是什么

后缀数组是一个整数数组，用来表示某个字符串所有后缀在字典序中的排序。

  • sa数组

后缀数组又称为sa数组（Suffix Array），其元素表示原字符串各后缀在字典序中的位置排序。

如果字符串S的后缀树组为sa，那么sa[i] 表示S中第i小的后缀在原字符串中的起始位置。

  • rank数组

与sa数组对应的是rank数组，它表示每个位置上的后缀在后缀数组中的排名。

如果字符串S的后缀树组为sa，那么rank[i]表示以i口头的后缀在后缀数组中的排名。

  • 两者关系

根据上面的定义，我们可以知道，rank数组是sa数组的逆数组，也即是：

rank[sa[i]] = i，sa[rank[i]] = i

我们通过 banana 这个字符串来演示 sa数组 以及 rank数组的工作原理

  • step1：构建所有后缀并按字典顺序排序

列出 “banana” 的所有后缀

    0: banana
    1: anana
    2: nana
    3: ana
    4: na
    5: a

按字典顺序排序后

    5: a
    3: ana
    1: anana
    0: banana
    4: na
    2: nana
  • step 2: 构建后缀数组 SA 和 rank 数组

根据排序结果，构建sa数组 ：

    SA = [5, 3, 1, 0, 4, 2]

构建 rank 数组：

    rank[5] = 0
    rank[3] = 1
    rank[1] = 2
    rank[0] = 3
    rank[4] = 4
    rank[2] = 5

因此 rank数组为：

    rank = [3, 2, 5, 1, 4, 0]

再来看一个例子

img

能解决什么

后缀数组+rank数组 可以接解决非常多的字符串问题

还能去做RMQ问题，也即是Range Maximum/Minimum Query 的缩写，表示区间最大（最小）值

关键点在于后缀数组怎么样形成最方便

image

后缀数组的地位

它的地位非常高, 很多的问题都是由 后缀树 或 后缀数组 实现的

后缀树 实现 跟后缀数组实现的区别

后缀数组可以替代非常多后缀树的内容

因为后缀树生成是更麻烦的一个东西

我们用后缀数组可以代表字符串的一些后缀信息, 可以解决很多字符串的问题

后缀树案例说明

后缀字符串

从开头开始往后所有都要

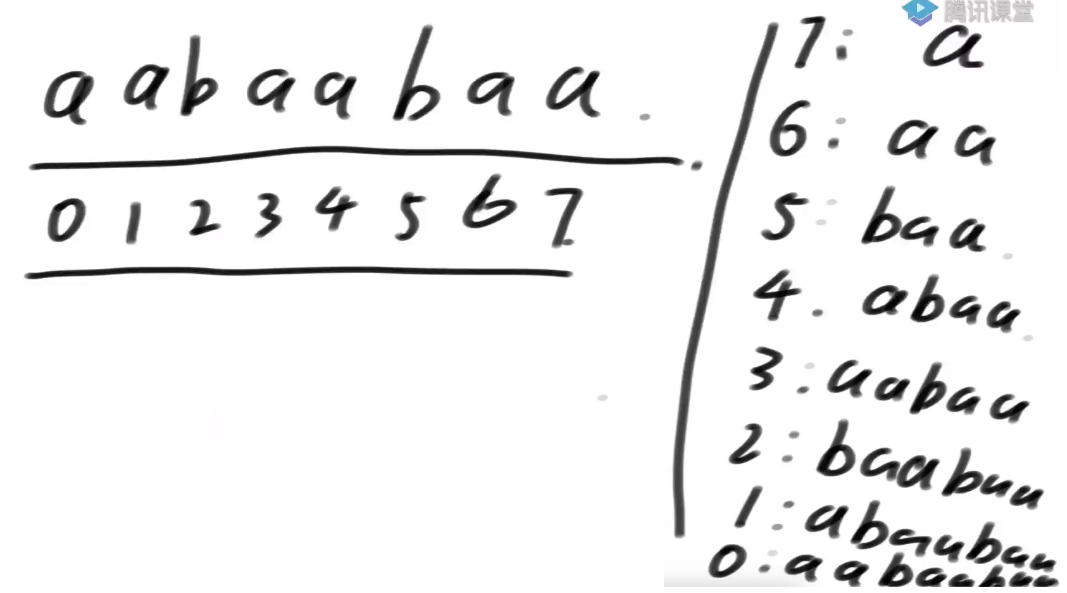
image

对所有后缀字符串做典序排序

所谓的后缀数组它其实代表所有的后缀字符串在排完名之后，从第0名到第7名依次写下来，这就是所谓的后缀数组

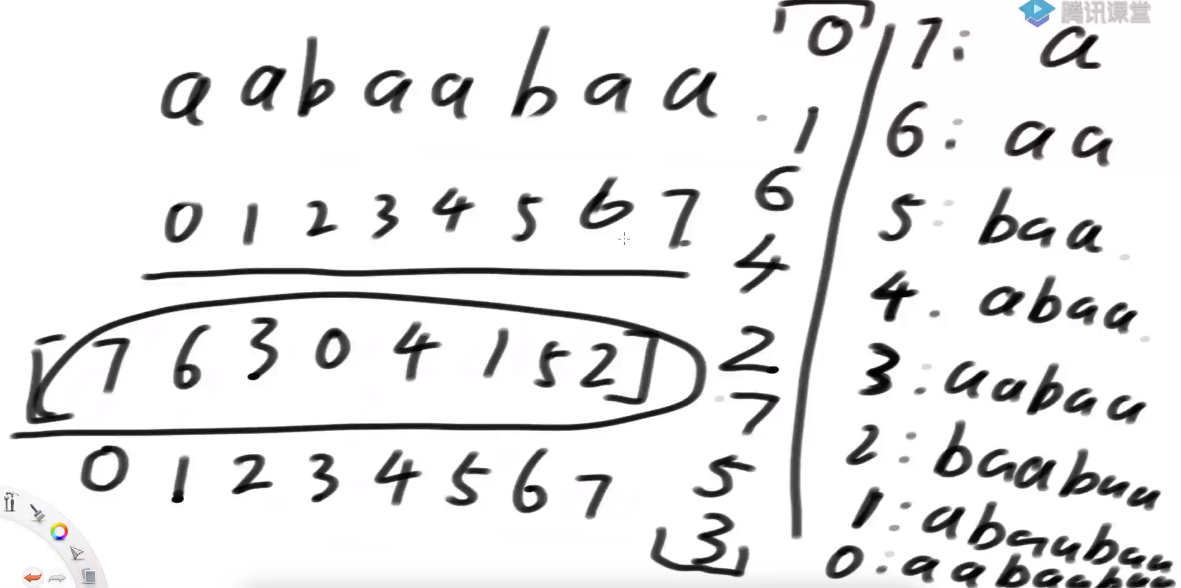
image

注意一点：不会有排名相同的，因为所有后缀串的长度不同

怎么样生成排名

先看一下暴力方法生成的流程

  • step1：先生成所有的后缀字符串, 复杂度O(N^2)

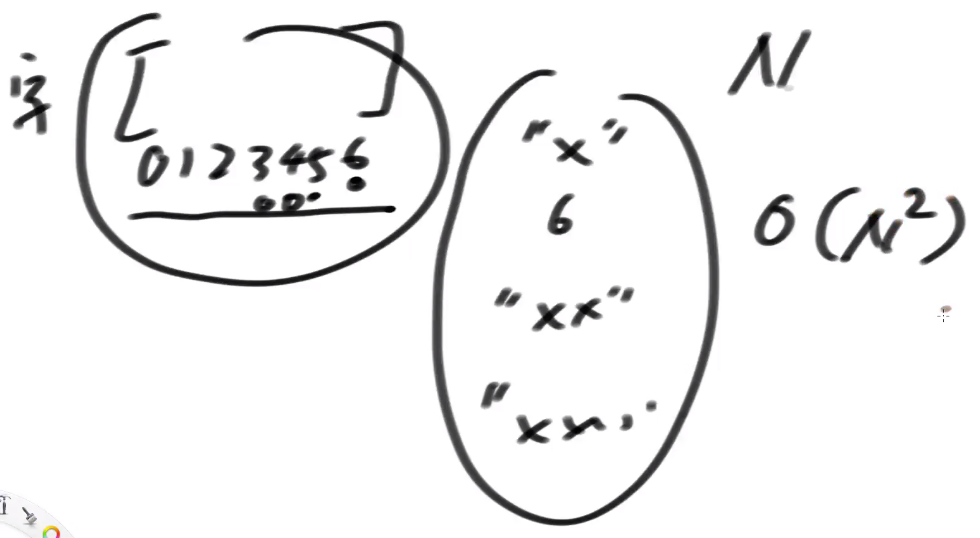
image

  • step2：后缀字符串数量 O(N), N个后缀字符串排序, 代价O(N*logN)

两个字符串比较大小的复杂度是O(1)吗? ==> 和字符串的长度有关，后缀串的平均长度O(N)

暴力生成的复杂度

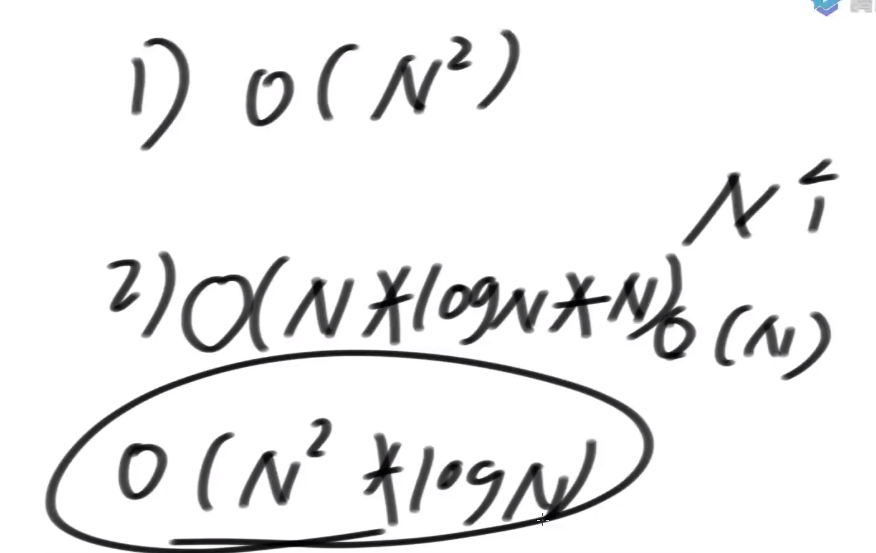
image

暴力方法生成后缀数组

  • 生成所有的后缀串

光生成后缀数组的字符串数组代价就已经是O(N^2)了

后缀字符串的数量是O(N)的

image

  • 给定长度为N的字符串

1）生成所有后缀数组的字符串数组, 复杂度O(N^2), 也是N

image

2）排序, N*logN, 但问题是这里的排序是两个字符串直接比较大小

字符串的平均长度是N/2

把字符串数组排好序, 单个两个字符串比对的代价O(N)

字符串排序的代价是O(N^2*logN)

是一个很痛的瓶颈

image

DC3算法引入

上面暴力方法说明生成后缀树时，字符串间的字典序比较是一个耗时操作，我们需要寻求是否有一种算法来优化这一部分内容。

于是DC3算法应运而生，它能够做到时间复杂度为 O(N) 解决上面的问题。

其核心思想：根据下标模3来分组, 做了一个类似于递归的事情来把这个问题解决的。

后缀数组的复杂度跟要求

后缀数组可以做到生成复杂度: O(N)

但是有一个前提：初始时, 数组里头每一个的值不要太大

如果非常大, 下面的方法就不合适了, 常数项就会有点大

image

回顾：基数排序

比如所有的数字都是三位

  • step1：先按照个位数进桶

image

  • step2：从 0~9 顺序从桶中拿出数字来，然后按照十位数字进桶，后进的权重更大

  • step3：重复step2，直到最高位

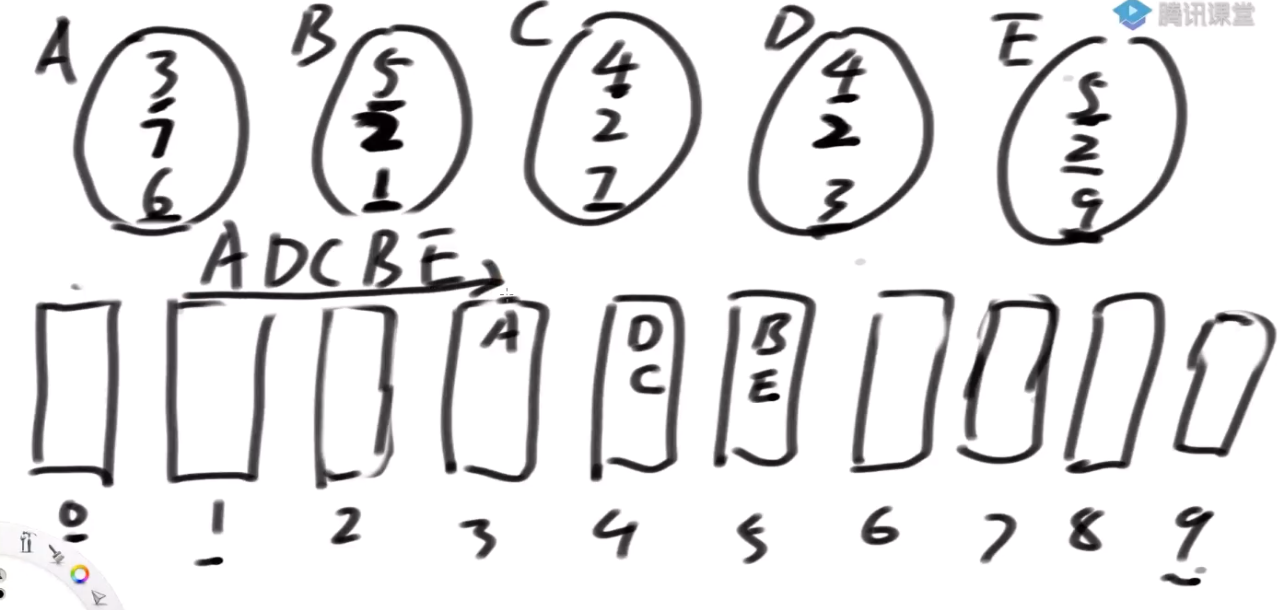
image

这里我们可以做一个升级, 有两位数据, 每一个数据有两个指标

56, 4 : 56 算一位, 不要拆开

对上面数据排序

3-7 最前 17-79 第二 23-34第三位 最后56-4

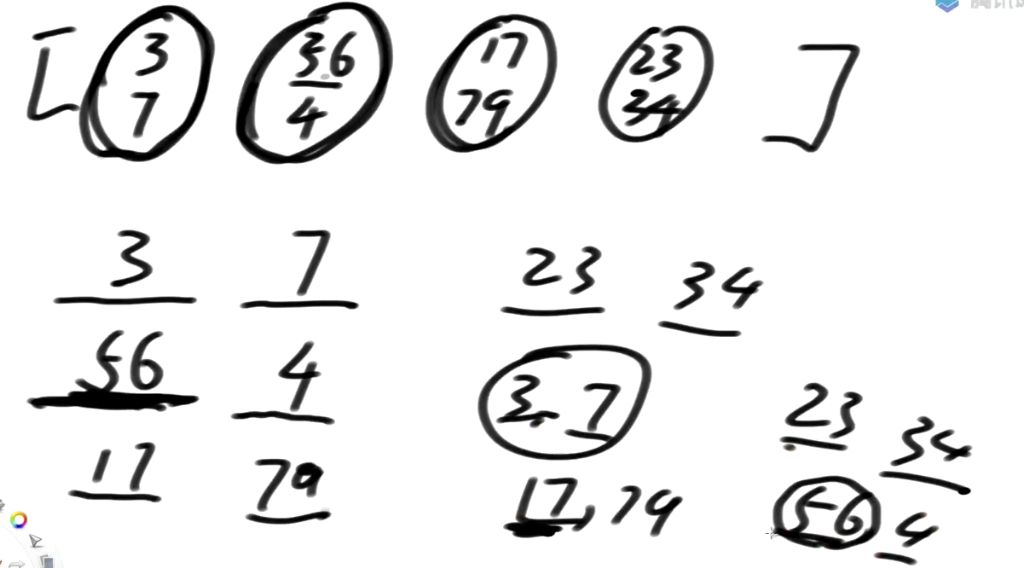
image

如果N个样本, 数据的维度不超过3维, 而且每个维度的值相对较小(比如1000以内)，否则基数排序的常数项极大

则N个样本排序的代价可以做到O(N)

image

如果一个数据有3维信息, 每个位置的值不会特别大的话,

如果有N个数据, 排完序的代价还是O(N)的

前提是每一位上的值不要太大

image

再谈后缀树组

把字符串可以认为是一个数组, 每个位数据是这个字符串的ASCII码

=>可以把一个字符串求后缀数组，等同于对一个数组在求后缀数组。

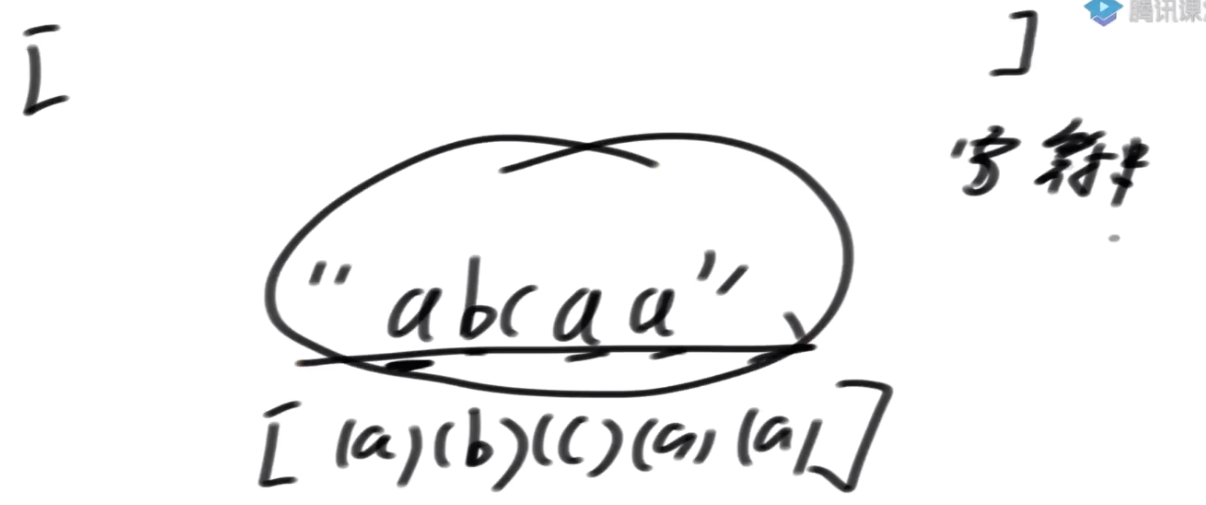
image

所以字符串可以求后缀数组,对于单独数组来说也可以求后缀数组

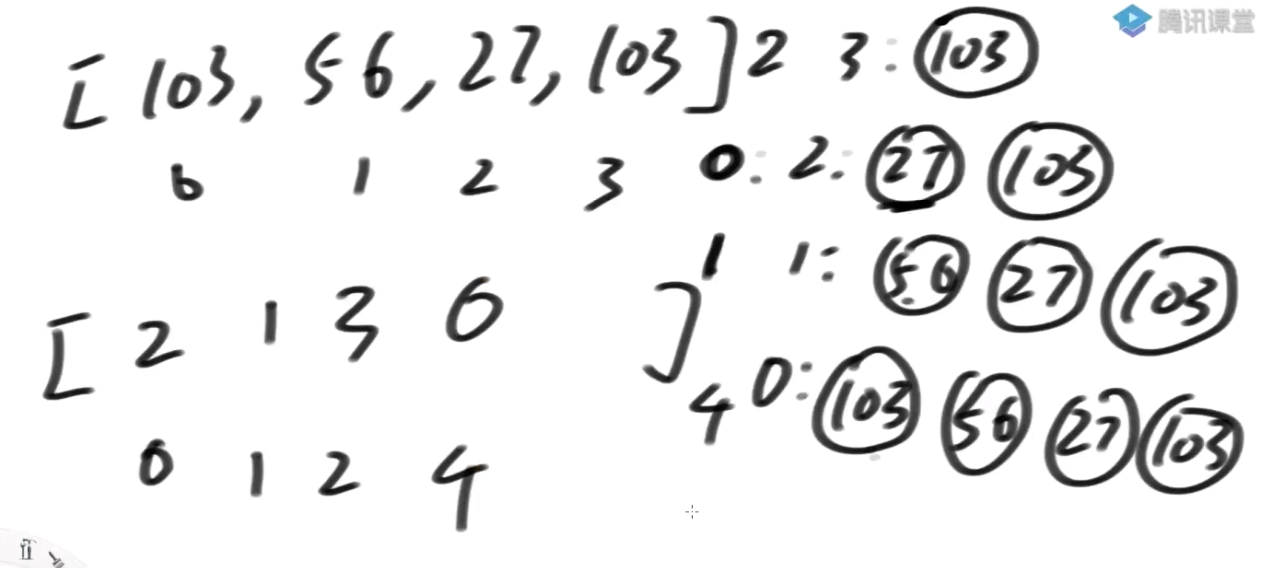
image

背景介绍

比赛中常用的后缀数组生成算法，时间复杂度最优的解是DC3算法，复杂度为O(N)

但是由于后缀数组一般耗时很久，所以比赛中的测试数据不会给的很高，选手也常用倍增算法解决, 它的复杂度为O(NlogN), 但是常数项优秀（从上面的介绍中可以看到，DC3算法使用了基数排序，常数项其实是很差的）。

image

扯得有点远，我们说回到 DC3算法。

DC3算法思路

下标分类

  • 首先, 按 索引对3取模 做下标分类

i%3== 0 ==> 0类下标, 代号s0类

i%3== 1 ==> 1类下标, 代号s1类

i%3== 2 ==> 2类下标, 代号s2类

所有后缀字符串, 长度不一样, 所以不会有后缀串排名一样

image

S12推出S0内部排名

假设有一个非常方便的方法 先把S1, S2类的后缀数组排名求出来（后面展开，这里先把S12当做一个可以使用的黑盒）

我们能不能得出所有0类, 1类, 2类下标的整体排名?

所有3类混在一起的下标排名能不能通过S1, S2类的已经出来的信息,给它都加工出来？

image

怎么使用S1,2类的信息呢?

先看看S12类能不能把S0内部的排名搞定

image

字符串不相同的情况

  • 0开头的a

  • 3开头的a

  • 6开头的c

如果只看一个字符, 6的排名是不如0,3的

这个过程可以用基数排序

s0内部的首字母不一样, 根据首字母就可以划块了

首字母不一样的块之间的排名, 我一定能求出顺序

下面的问题就是0,3开头,这些同样在一个块内部的这些后缀串怎么排名?

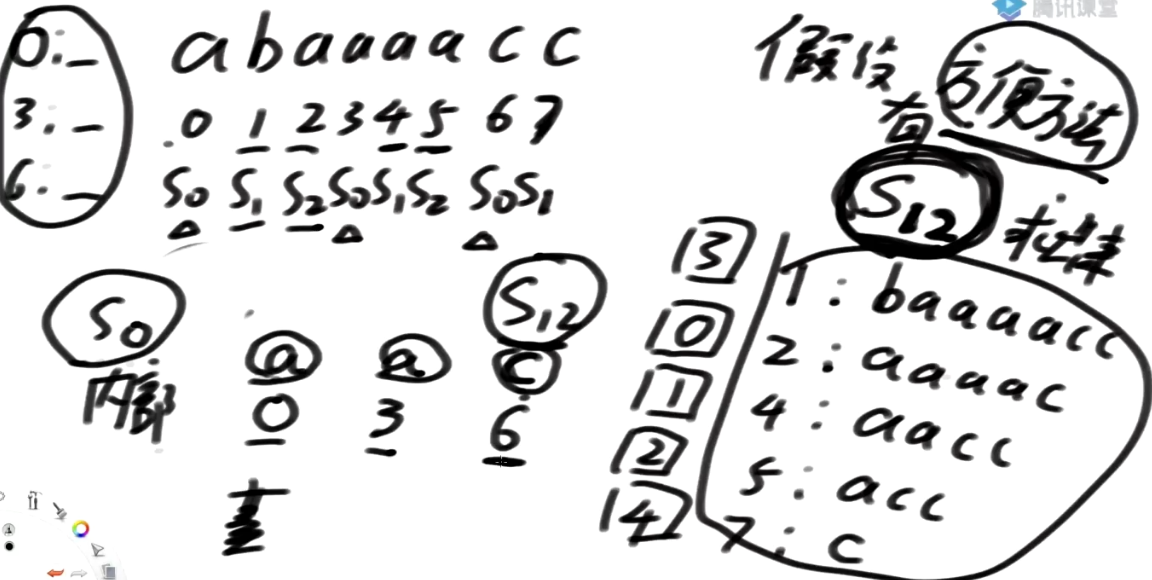
image

  • 0开头的字符是a，后面的是1开头及其后面所有，S12中1开头的排第3位，因此S0中记为a_3

  • 3开头的字符也是a，后面的是4开头及其后面所有，S12中4开头的排第1位，因此S0中记为a_1

在S12中：1开头及其后面的所有 跟 4开头及其后面的所有的总排名我们是知道的

虽然第一维数据一样, 但是0开头的 a_3 是干不过3开头的 a_1

依然可以基数排序, 过一遍决定顺序, 时间复杂度O(S0的大小)，也即O(N/3)=O(N)

还是基数排序, 相当于一个对象 两位的信息

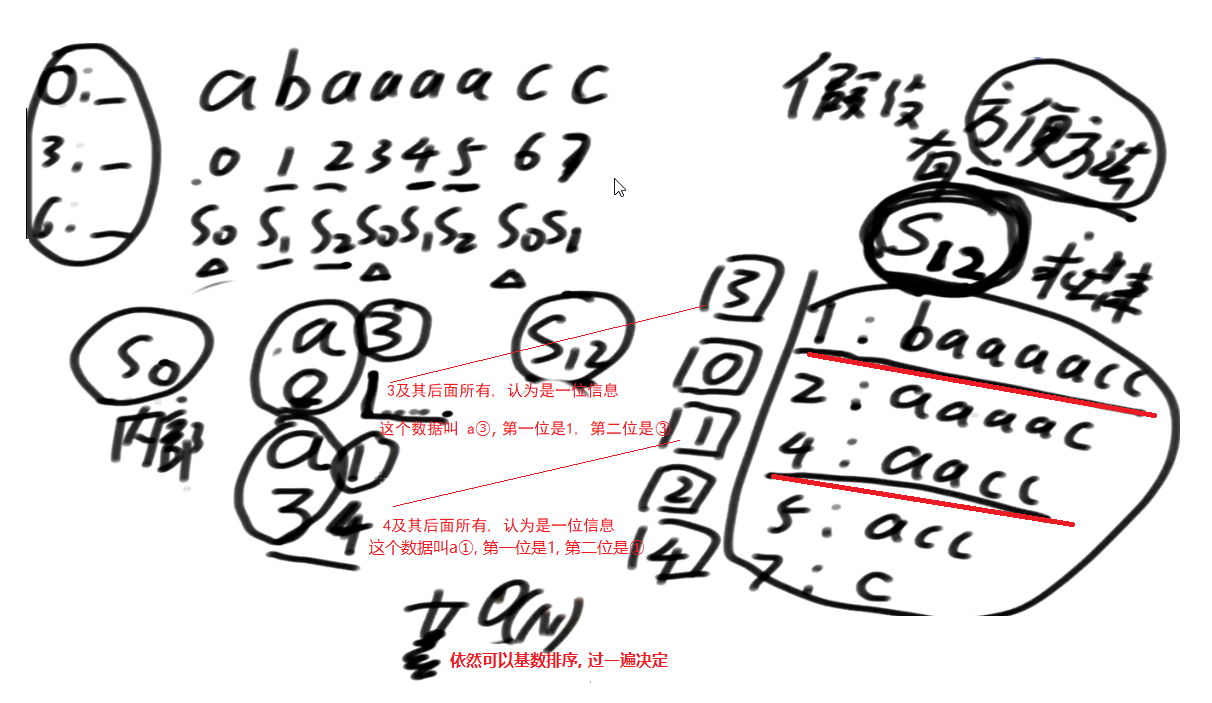
image

S12与S0的Merge

由上面的推导可以知道，如果已知S12，那么可以在O(N)的时间复杂度内推出S0。

接下来，自然而然地想到，如果需要得到整体排名，我们只需要得到 S12与S0的merge策略。

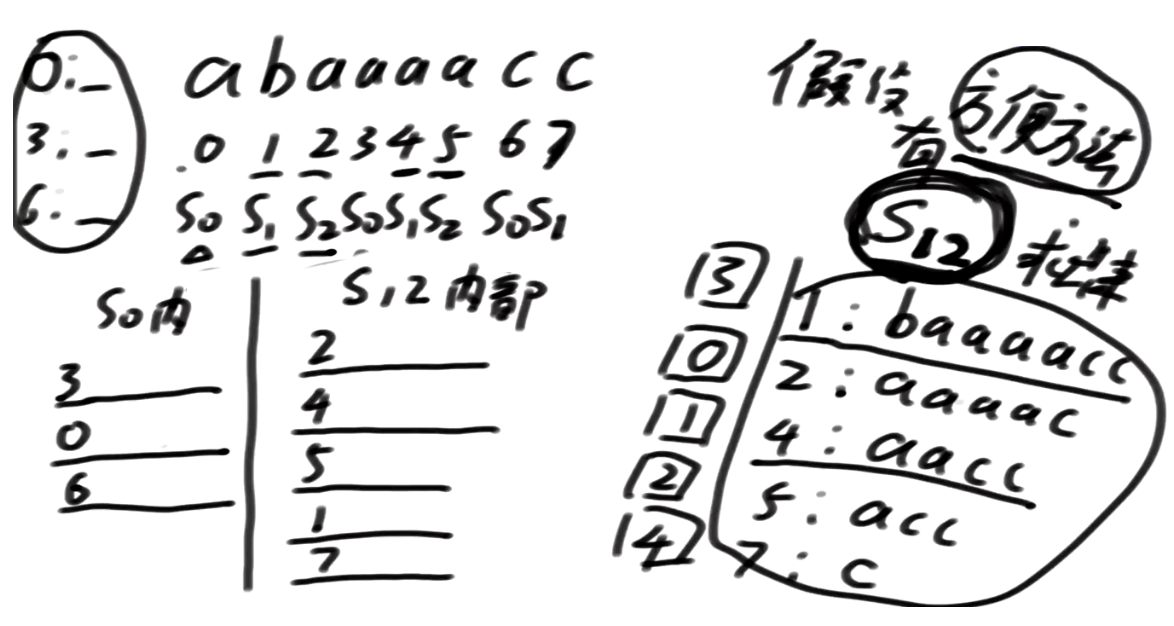
image

3 开头的 跟 2开头的谁小谁排出

依次从上往下, 如果我们存在merge策略

总排名就出来了

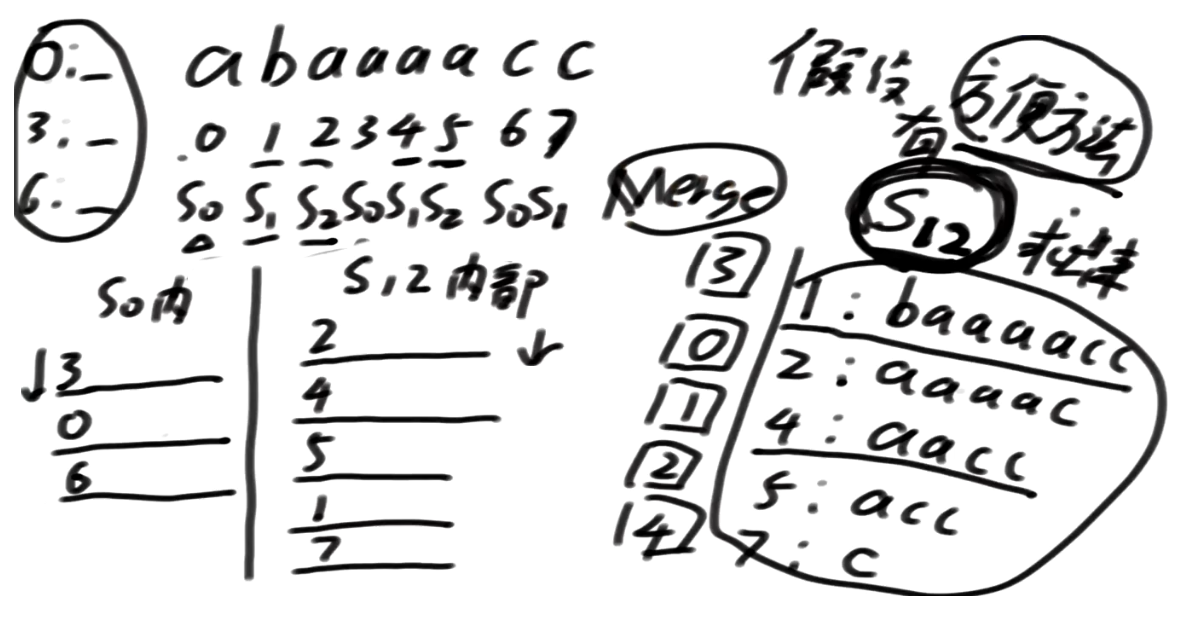
image

怎么进行merge呢?

我们先整体审视一变，同常规的 归并排序，或者说 map-reduce的reduce过程类似，由于S0以及S12都是有序的，我们只需要在S0以及S12侧都给到一个指针（表示在S0以及S12中数组的索引），逐一比较大小即可。

不妨设S0此时指针来到 p0，S12指针此时来到p12，如果p0指向的索引开头的字符以及p1指向的索引开头的字符不同则直接可以比较大小，我们不用进行后面的操作了。

如果 p0 以及 p12 指向的索引对应的字符相同，我们需要分情况讨论：

  • 1）假设p12此时指向的是S1，例如 p0 此时指向6，p12此时指向10，那么只需要再向后看一位就一定可以知道排序，由于p0后面一位的字符为第7位以及后面所有的字符，而p12后面一位的字符为第11位以及后面所有的字符，我们知道 7和11的位置都在S12中，而S12的总体排序又是知道的，那么直接判断即可。

  • 2）假设p12此时指向的是S2，例如 p0 此时指向6，p12此时指向11，那么只需要最多再向后看两位就一定可以知道排序，由于p0后面一位的字符为第7位以及后面所有的字符，而p12后面一位的字符为第12位以及后面所有的字符，如果第7位以及第12位字符不同，那么第6位以及第11位的后缀数组的字典序也必就能比较出来，如果还是相同，由于7在S12，而12在S0，不能直接比较，但是再往后看一位，6后面的第二位为8，11后面的第二位为13，8和13的位置都在S12，可以直接比较，那么6和11的顺序也就出来了。

总结一下：

  • 如果p0以及p12指向索引的字符不同，直接出结果

  • 如果p0以及p12指向索引的字符相同

    • p12位置为S1，再向后看一位出结果，加上当前位，也就是最多看2位就能出结果

    • p12位置为S2，最多再向后看两位出结果，加上当前位，也就是最多看3位就能出结果

也就是 merge 中每一步的比较时间都是 O(1) 的

下面还是看上面的具体案例

一开始 3 开头的 跟 2开头的 pk

  • 3开头的上面字符是a

= 2开头的上面字符也是a

所以要再往下比较, 都是a, 又比不出来

再往下

  • 考察5及其后面的整体

  • 和4及其后面的整体

这俩排名在s12里有 ==> 最多三维信息可以搞定merge，只用比三个位置的信息就可以决定3开头跟2开头谁大谁小

这都不是基数排序，就三个位置的值比较一下

image

3是一个s0类的下标, 遭遇的是2 s2类的下标

当S0类下标在merge的时候遭遇了S2类下标跟它pk的时候, 往后要比三位

S0 跟 S2下标pk的时候, 最多拿三个位置的数比一下, 就知道怎么merge了, 谁大谁小就出来了

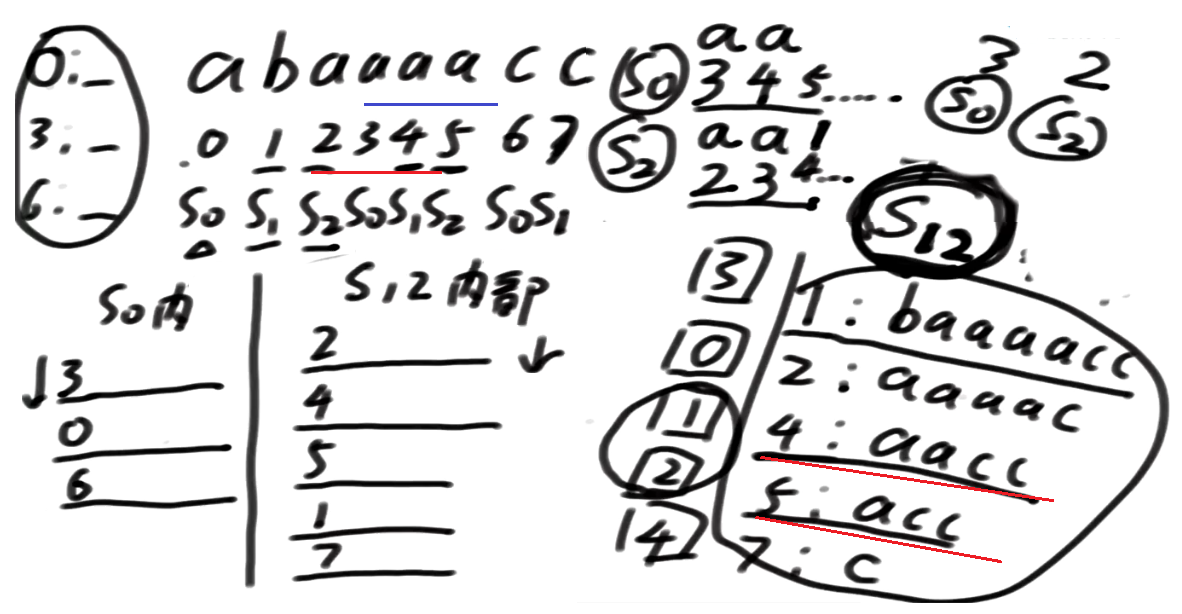
image

后面的信息, 3开头的是 2, 2开头的是1, 3开头的没pk过2开头的

2开头的就是所有下标开头的Number0

接下来3开头的跟4开头的pk

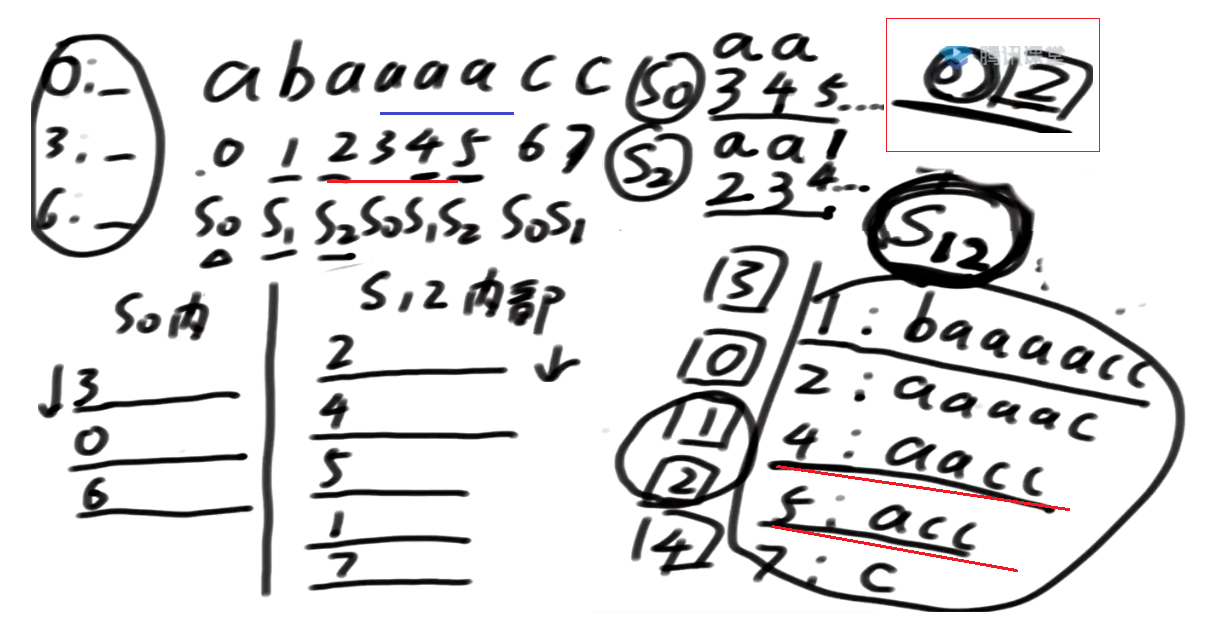
image

怎么样pk3开头的跟4开头的?

  • 3开头的是s0类型

  • 4开头的是s1类型

当S0类 跟 S1类下标pk的时候, 最多比两个位置的数

3位置是a, 4位置也是a

接下来比4及其后面的整体 和 5及其后面的整体

这俩排名在s12内部的排名是有的

所以S0类 跟 S1类下标pk, 最多比两个位置的数, 可以决定大小

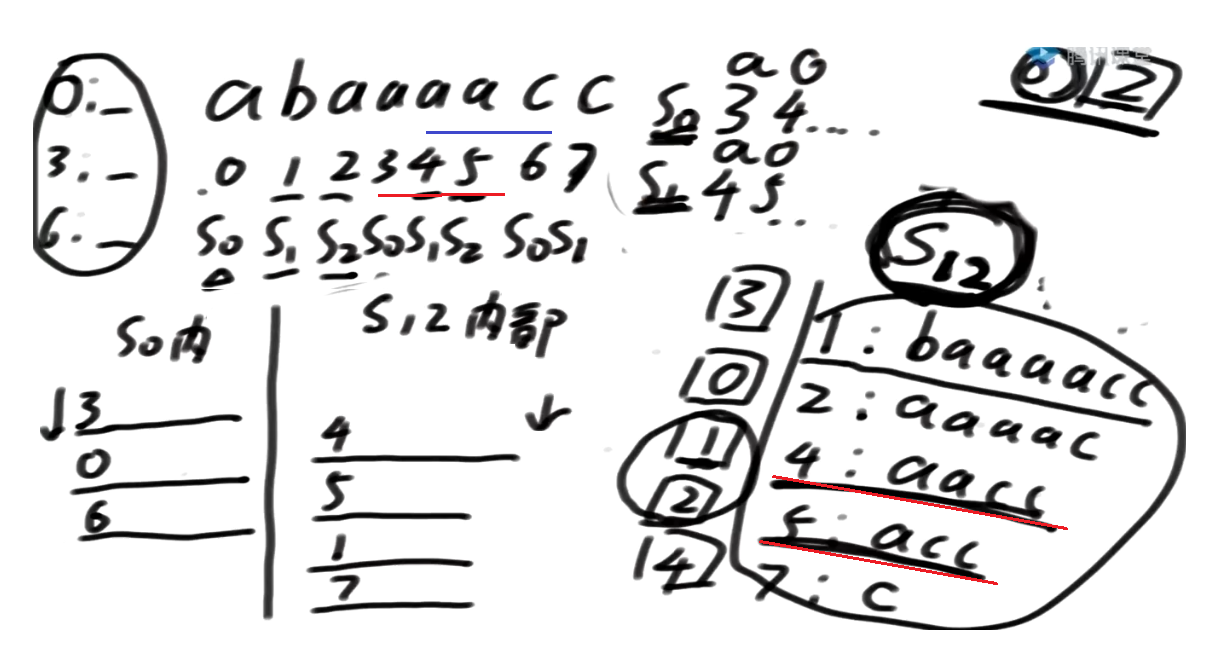
image

DC3算法实现

总体流程

首先字符串长度N

  • step1：有一个f()函数 帮我得到S12内部的排名

  • step2：用s12 的信息得到s0内部的排名

    • 使用基数排序: O(N)

  • step3：把S0 跟 S12去merge, 又利用到s12类的信息, 都排出来,时间复杂度: O(N)

step2以及step3的求解过程上面已经说明了，后面就不赘述了

可以看到, 整个流程中成败的关键就是第一步, 后面两个过程都是O(N)的过程

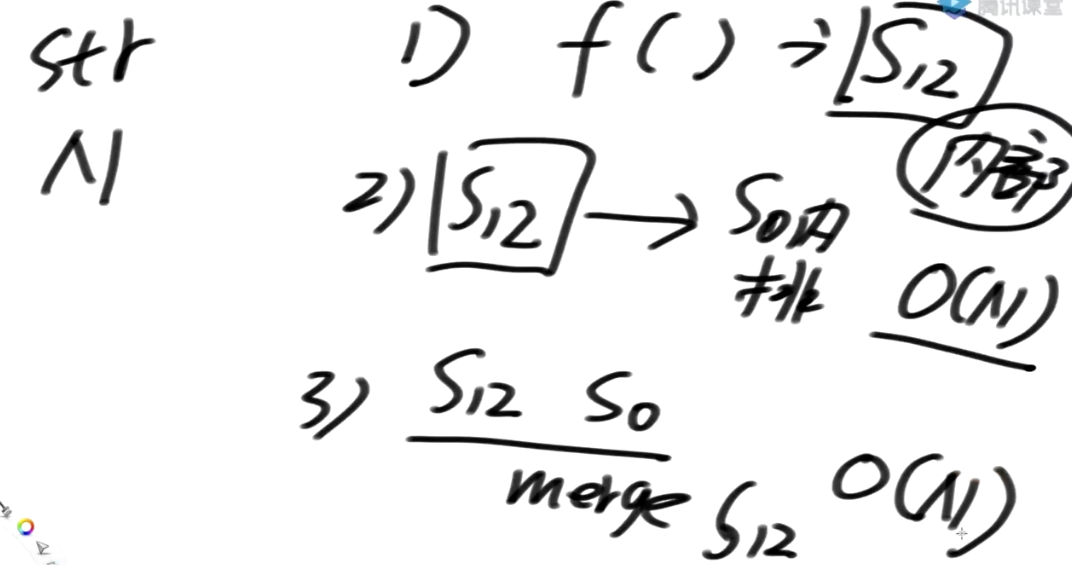
image

如何得到S12类的排名

处理流程

要求这个排名一定要是精确的，里面不要有重复值

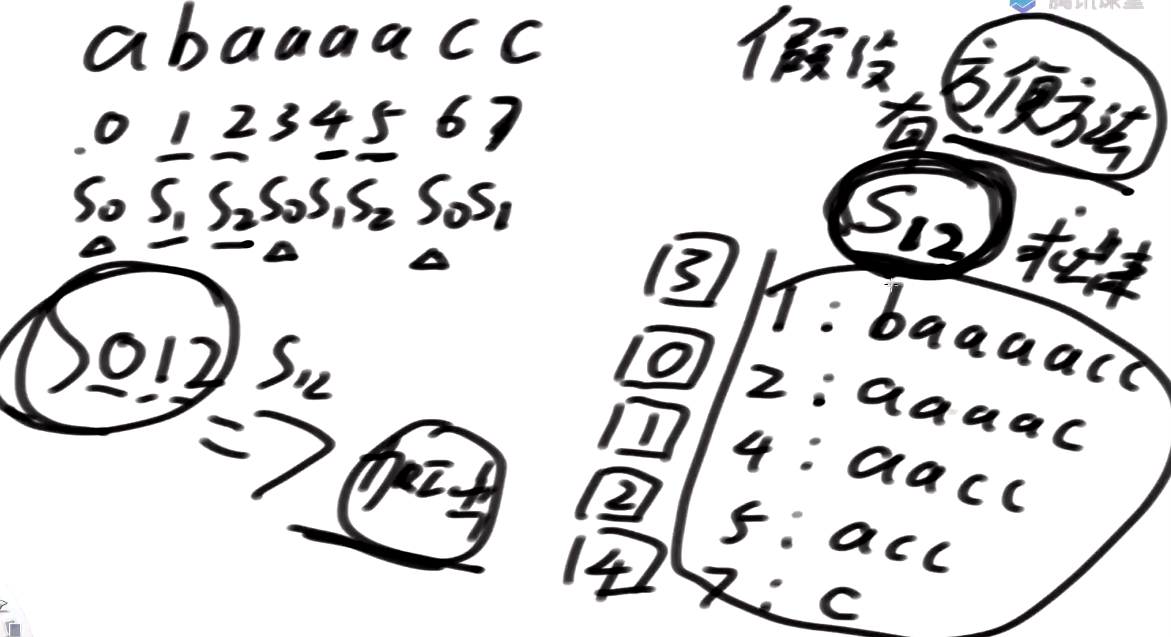
画下划线的就是s12类

先这么想，怎么决出下面的整体排名

  • 1开头及其后面的所有

  • 2开头及其后面的所有

  • 4开头及其后面的所有

  • 5开头及其后面的所有

  • 7开头及其后面的所有

  • 8开头及其后面的所有

  • 10开头及其后面的所有

  • 11开头及其后面的所有

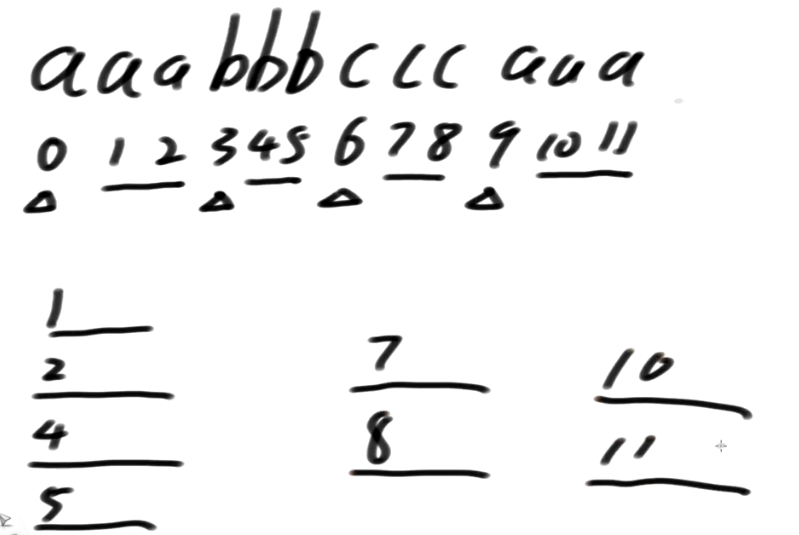
image

先只拿前三维信息做比较，如果此时字符不够3位了，用极小值来填充

  • 1开头前三个字符aab

  • 2开头前三个字符abb

  • 4开头前三个字符bbc

  • 5开头前三个字符bcc

  • 7开头前三个字符cca

  • 8开头前三个字符caa

  • 10开头前三个字符aa0

  • 11开头前三个字符a00

这个例子展示的是：如果我们仅拿3位信息就足以得到严格排名的话, 那岂不爽哉

那么这样的话只需要经过一个O(N)的基数排序就拿到S12了，接下来可以直接去做后面2,3的步骤

现实情况是： 有可能只拿前三位信息它排不出严格的排名

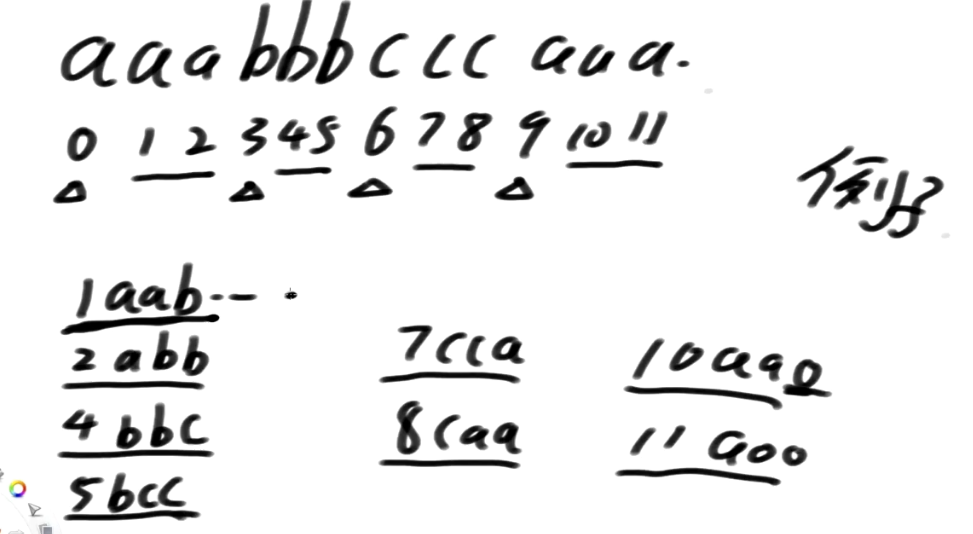
image

我们拿mississippi这个单词来做说明（注：这个是DC3论文中作者的提过的案例）

只拿1,2类信息的前3维信息 能不能得出精确排名呢?答案是不行滴 o(╥﹏╥)o

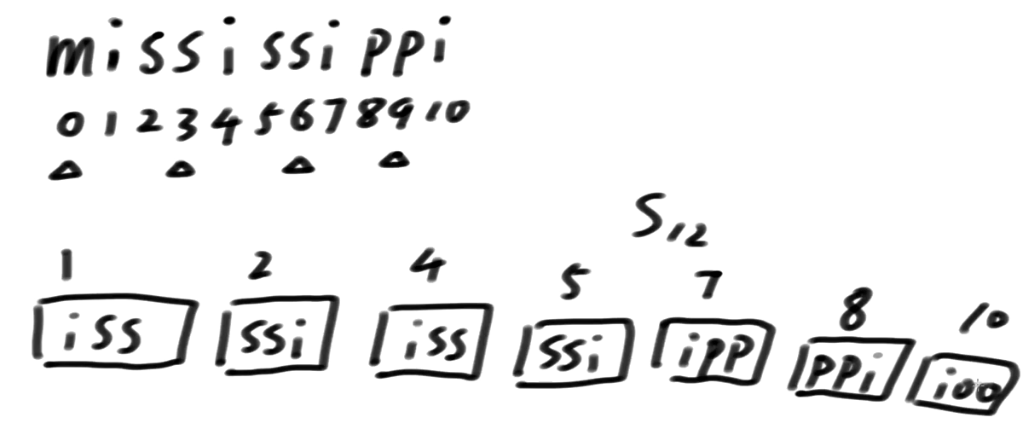
image

这样的话, 我们就没有决出精确排名

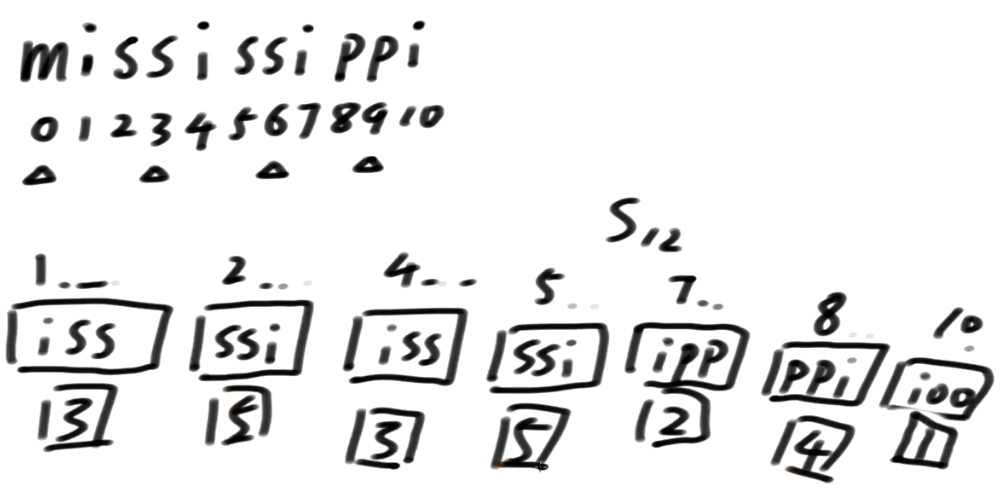
image

好了，整个算法中最精髓的部分，它来了！！！

生成一个数组:

  • 把S1类整体放在数组左边

    • S1类所对应的排名放数组左边

  • 把S2类全放在数组右边

    • S2类所对应的排名放数组右边

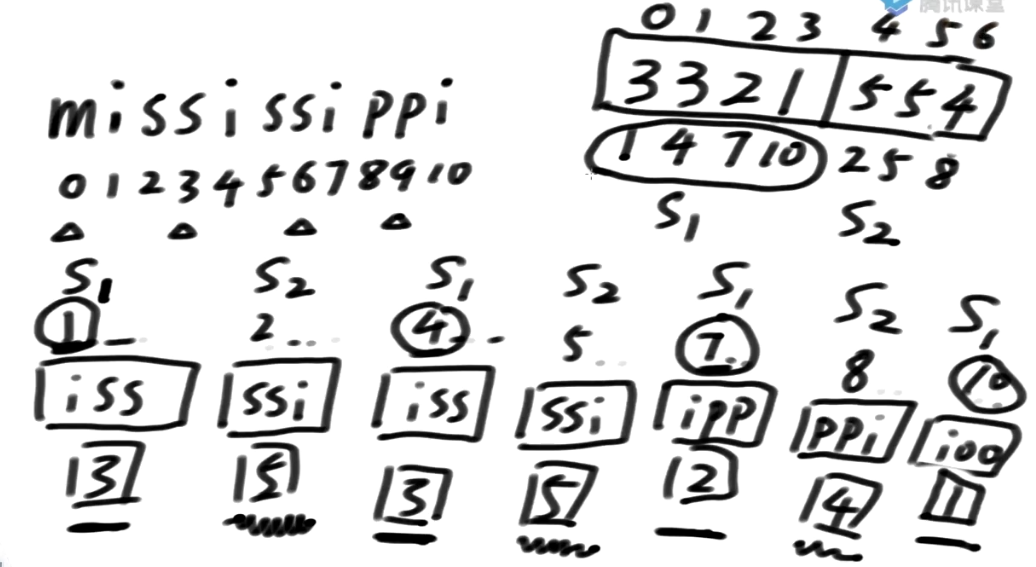
image

获取结果

我们把这个数据认为是个字符串数组，递归的调用求它后缀数组的排名

求出来了哪个是第一名?

1554, 3位置是第一名, 对应会原数组中10 它是第一名

下面是2开头的 21554, 对应会原数组中7 它是第二名

接下来是321…, 是原数组第1位置

接下来是3321…, 是原数组第0位置

接下来是4, 是原数组第6位置

接下来是54, 是原数组第5位置

接下来是554, 是原数组第4位置

后缀数组的这个结论求出来以后, 它可以对应回原来我想求这个东西里面的s12类的排名！！！

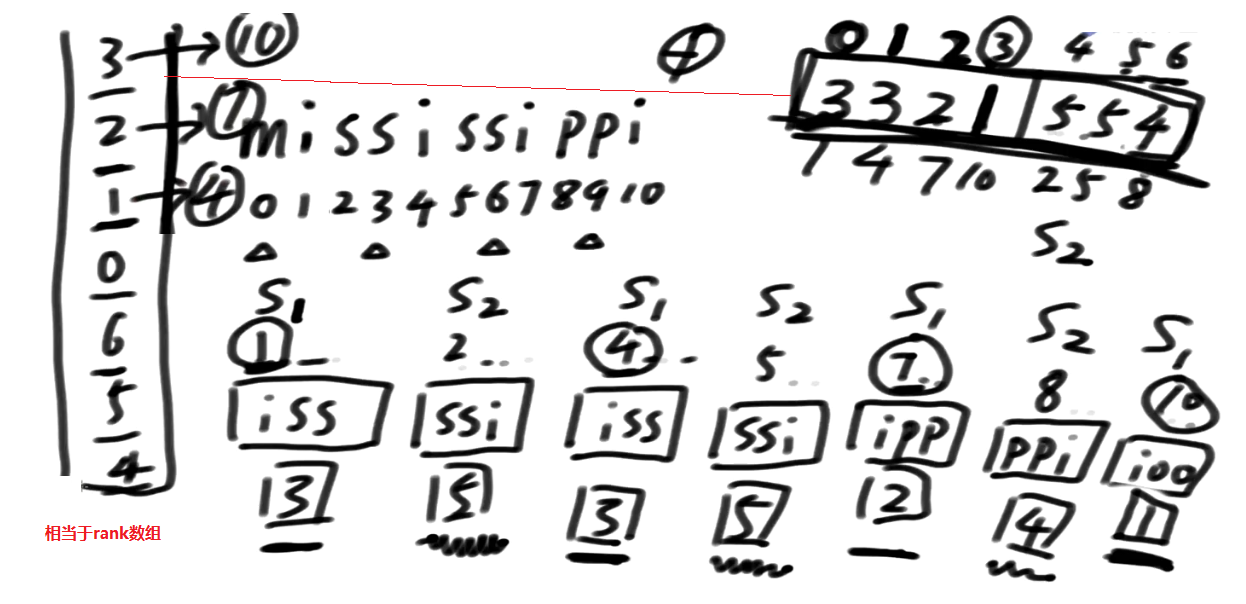
image

结论解释

一开始有一个比较粗糙的排名, 没有得到精确的排名,比如说 有两个3, 两个5

如果你把这个排名的值当做是字符的话, 我这个1不可能在排完字符串之后排名往后掉

相当于我首字母就是1，首字母如果划分出块了, 即便后面怎么摆, 也不会让排名乱掉, 块与块之间排名不会乱掉

为什么要这么摆?这么摆可以把同一块内部的排名搞定!

先看两个相同索引同时落在S1或者同时落在S2的情况

看这个两个3

3: 1开头及其后面的所有

3: 4开头及其后面的所有

分不出来

因为我们只拿了前3位信息出来, 它们彻底相等, 所以区分不出来

接下来, 你需要什么信息?

3: 123 4开头及其后面的所有

3: 456 7开头及其后面的所有

s1类摆在整体左边, s2类摆在整体右边

对于同一组内部, 这么摆, 正好这个结构关系能帮它区分排名

image

5: 234 5开头及其后面的所有

5: 567 8开头及其后面的所有

这个例子展示的是, 相同的排名信息落在一组里的情况, 都落在左组或者都落在右组

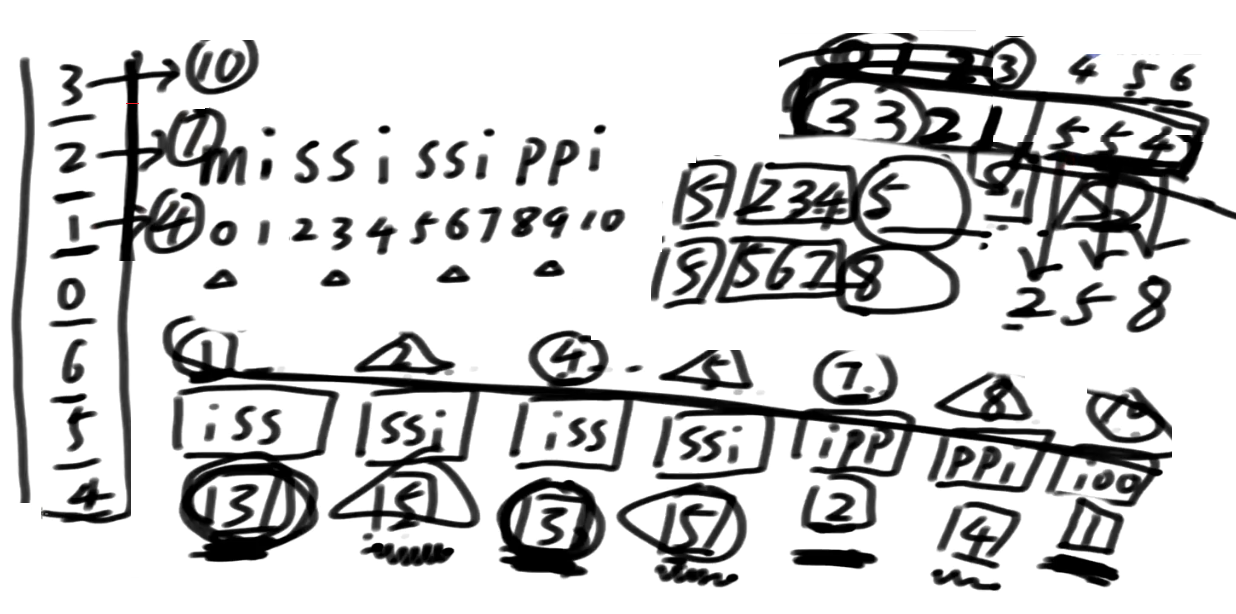
image

那如果相同的信息落在不同组呢？

其实相同的排名即便是跨组, 这么摆, 也能搞出区分来

比如说原始位置为1和5的两个位置，它们在非严格区分排名中都是第3名

看看下一位的信息：

123，下一位为4，在新数组中紧靠着1，假设排名为x

567，下一位为8，在新数组中紧靠着5，假设排名为y

那么现在需要比较 3_x 以及 3_y的大小，这个显然与新数组的后缀树的排名仍然是保持一致的。

那么也就是说无论相同信息落在同一组还是不同组，都能验证上面的结论。

S1及S2交接位置处理

现在还有一个小坑：S1类以及S2类交接的位置相同时如何比较排名

这里如果S1的最后一位本来就补了0，那么S2中的数顺着S1往后一定可以找到不同的3位后缀

如果S1的最后一位实在无法补0，那我们人为给S1补一个000

  • 假设长度 % 3 == 2

S1的最后一位会补0，因此S2中的后缀值一定能够与它分出胜负

比如说长度为11，索引为 0~10，10的3位后缀，后面有两位用0补了

那么索引为2的后缀 与1、4、7 相等时，1、4、7对应的后缀为 4、7、10及后面的数字，这个其实在SA12中都有了，而且值也是正常的，唯一有点差异的是 索引为 10的，假设 num[2] = num[10] = 5，那么2的三个数的后缀位 5xy，x>0，y>0，而10的三个数的后缀位为500，基数排序时已经分出胜负了

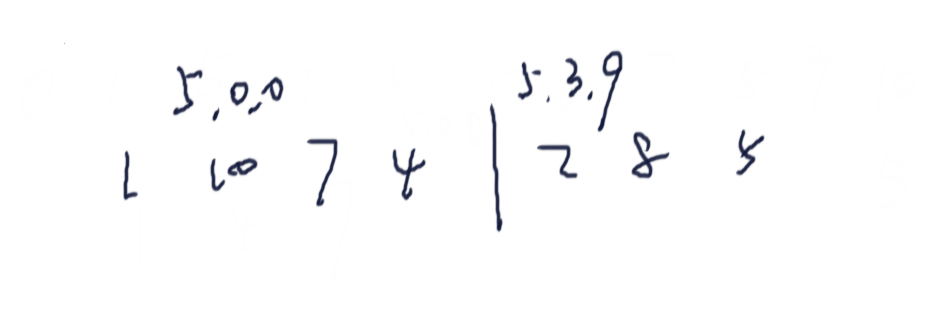
image

  • 假设长度 % 3 == 0

情况与 长度 % 3 == 2 类似，此时 S1的最后一位会补0，S2中顺着S1至少可以找到一个不同值。

比如长度为9，索引为 0~8，S2前面的值与S1比较逻辑与上面的类似，如果是索引为8和索引为7的3位后缀进行比较，假设在这两个索引上的数字都是5，那么7对应550，8对应500，基数排序后 7 本来就在8的后面。

最低0.47元/天 解锁文章
【电力电子】SPWM（正弦脉宽调制）技术的深度解析(等效面积，单极性/双极性SPWM,谐波)
Naiva的博客
06-10 771
是。
[YOLOv8] 基于yolo的原神鱼群目标检测
weixin_44349241的博客
01-10 2208
基于yolo原神鱼群目标识别效果
DC3算法生成后缀数组详解
明朗晨光的专栏
04-10 1297
何为后缀数组；基数排序；使用DC3算法生成后缀数组
算法数据结构（三十八）----DC3算法
u011624267的博客
09-13 1813
后缀和数组 后缀数组其实代表所有的后缀字符串在排完名之后，从第0名到第7名依次写下来，这就是所谓的后缀数组 不会有相同的排名，因为长度不一样 生成后缀数组 1)暴力求解： 先生成所有的后缀字符串，复杂度O（N^2） 后缀字符串数量O（N），N个后缀字符串排序，代价O（N*logN） 2）DC3求解：O（N） 根据下标模3来分组，做了一个类似于递归的事情把这个问题快速解决，有一个前提，初始时，数组里头每个...
【Vulnhub系列】DC3
大方子
04-08 5208
文章目录基本信息实验过程额外补充利用php反弹shell使用Linux-Exploit-suggestion来辅助提权 靶机下载地址：https://download.vulnhub.com/dc/DC-3-2.zip 基本信息 Kali:192.168.61.145 DC3:192.168.61.163 实验过程 同样先通过arpscan扫描找出DC3的IP地址 sudo arp-scan --interface eth0 192.168.61.1/24 这里可以直接看出DC3的IP地址为192.1
后缀数组_模板
hengfanz的专栏
03-13 530
倍增算法 #define maxn 1000001int wa[maxn],wb[maxn],wv[maxn],wws[maxn]; int cmp(int *r,int a,int b,int l) {return r[a]==r[b]&&r[a+l]==r[b+l];} void da(int *r,int *sa,int n,int m) {     int i,j,p,*x=w
【*】后缀数组（dc3算法构造）
famousDT的专栏
03-20 1789
const int Max = 200001; int num[Max]; int r[Max * 3], sa[Max * 3]; int rank[Max], height[Max]; int wa[Max], wb[Max], wv[Max], wd[Max]; #define F(x) ((x) / 3 + ((x) % 3 == 1 ? 0 : tb)) #define G(x) ((x
DC3算法(后缀数组生成)
xiaolu567的博客
06-27 1729
如果我要对数组排序的话,按字符串的字典序来排,这个就是后缀数组 以某个位置开始后面整体的后缀串,它在所有开头位置的后缀串中排名第几,把它自己的排名作为一个数组,返回跟它对应的就是rank数组(原始下标按字典序的排名) 后缀数组跟rank数组就是一种转换关系,后缀数组可以在O(N)的时间内转化为rank数组 rank数组可以在O(N)的时间内转化为后缀数组后缀数组+rank数组可以接解决非常多的字符串问题 还能去做RMQ问题 关键点在于后缀数组怎么样形成最方便它的地位非常高,很多的问题都是由后缀树或后缀数组实
近邻算法常用距离公式与推导（内附证明）初中生也能看懂
尼克不可的博客
05-03 3871
一. 欧式距离 其实这个名字听起来很高大上，但是其实你在初中的时候就用过，只是那时还没给他一个官方的名字，你肯定做过这样的题，在直角坐标系中给定两点A(x1,y1),B(x2,y2)A(x_1,y_1),B(x_2,y_2)A(x1​,y1​),B(x2​,y2​)然后让你计算两个点之间的距离。老师肯定也教过你过这个公式 d=(x1−x2)2+(y1−y2)2d=\sqrt{(x_1 - x_...
分子性质AI预测挑战赛｜Datawahle AI夏令营｜代码分享
最新发布
qq_42959513的博客
07-07 1276
在当今科技日新月异的时代，人工智能（AI）技术正以前所未有的深度和广度渗透到科研领域，特别是在化学及药物研发中展现出了巨大潜力。精准预测分子性质有助于高效筛选出具有优异性能的候选药物。以PROTACs为例，它是一种三元复合物由目标蛋白配体、linker、E3连接酶配体组成，靶向降解目标蛋白质。本次大赛聚焦于运用先进的人工智能算法预测其降解效能，旨在激发参赛者创新思维，推动AI技术与化学生物学的深度融合，进一步提升药物研发效率与成功率，为人类健康事业贡献智慧力量。
后缀数组DC3算法实现
weixin_30780221的博客
08-05 380
算法模板： View Code #define F(x) ((x)/3+((x)%3==1?0:tb)) #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2) int wa[maxn],wb[maxn],wv[maxn],ws[maxn]; int c0(int *r,int a,int b) {return r[a]==r[b]&&...
算法与数据结构31：DC3算法生成后缀数组
weixin_43889578的博客
12-11 1242
假设有字符串 aabaabaa那么从每个位置开始，到结尾位置，截取后缀串，可得aaabaaabaaaabaabaabaaabaabaaaabaabaa然后根据字典序对后缀串进行排序，排序结果放入数组中，数组中的值表示后缀串的开头位置那么这个数组，就是后缀数组对一个字符串求后缀数组，求实就是对一个数组求后缀数组，因为字符串里面每个字符都对应衣蛾ASCII码，也就是一个ASCII码数组假设有数组那么后缀串就是10327 103。
DC3算法模板学习笔记
qq_36172410的博客
05-04 1221
今天看了一下洛谷sx视频，后缀数组双关键字排序瞬间秒懂，昨天刚了一下午没有看懂的后缀数组基数排序代码有了一点点突破。 对第二关键字桶排序，保持相对顺序不变，则个位数字有序，对第一关键字桶排序，由于第一关键字相同情况下个位总是递增或持平，所以保持有序。 ——《高级数据结构》 #include<cstdio> #include<cstring> us...
实现后缀数组的倍增算法和DC3算法
始往流离，终彼成章。
03-22 4267
/************************************************ 数据结构：后缀数组(Suffix_Array); 子串: 字符串S的子串r[i..j]，i≤j，表示r串中从i到j这一段， 也就是顺次排列r[i],r[i+1],...,r[j]形成的字符串; 后缀： 后缀是指从某个位置i开始到整个串末尾结束的一个特殊子串; 字符串r的从第i个字符开始的后缀表示为
DC3算法相关题目
xiaolu567的博客
06-28 765
给定两个字符串str1和str2， 想把str2整体插入到str1中的某个位置 形成最大的字典序 返回字典序最大的结果每次拼出一个N+M的串N>>M,复杂度N^2 DC3算法解 那么,我们该如何把str2插入str1最好 在str1中如果i出发所有往后字典序>=str2字典序,str2没有必要插在i之前 如果每个位置开头字典序都大于str2, 那么str2放在最后 如果某个位置字典序小于str2的字典序,str2有可能插在i之前,也有可能在i之后i-1~i之间的可能性不可以忽略寻找一个范围最左的可能性~最
构造后缀数组的DC3算法实现
weixin_30457881的博客
07-19 229
DC3算法(Difference Cover mod 3)是J. Kärkkäinen和P. Sanders在2003年发表的论文 "Simple Linear Work Suffix Array Construction"中描述的线性时间内构造后缀数组的算法。相对Prefix Doubling（前缀倍增）算法而言，虽然它的渐进时间复杂度比较小，但是常数项比较大。DC3算法的思想类似于...
后缀数组dc3算法模版（待补）
weixin_30691871的博客
09-24 141
模版： const int maxn = 1000010; #define F(x) ((x)/3+((x)%3==1?0:tb)) #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2) int wa[maxn],wb[maxn],wv[maxn],wss[maxn]; char s[maxn]; int r[maxn],sa[maxn];...
poj2406 Power Strings 后缀数组 DC3算法
扬帆起航
02-11 955
Power Strings Time Limit: 3000MS   Memory Limit: 65536K Total Submissions: 46554   Accepted: 19489 Description Given two strings a and b we define a*b to be their concate
POJ2406 Power Strings 后缀数组(DC3算法)或KMP或暴搜(瞎写)
A confused programmer
10-14 410
方法一：暴搜。。（188ms） 自己瞎写的。。竟然过了？？！！！ 附上AC代码： #include&lt;cstdio&gt; #include&lt;cstring&gt; #include&lt;cmath&gt; #include&lt;iostream&gt; #include&lt;algorithm&gt; #include&lt;vector&gt; #include&lt;...
大白话解析Apriori算法：Python实现与原理
"Apriori算法是一种经典的关联规则挖掘算法，用于发现数据集中项目之间的频繁模式或关联。在Python中，它可以被实现来处理各种数据集，找出物品之间的潜在关联，如啤酒与尿布的故事所示。Apriori算法通过迭代生成...
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值