离散 第一章

原创 于 2022-06-10 17:41:48 发布 · 470 阅读 · 1 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#学习

离散 第一章

1.1集合的初见

朴素集合论
  • 集合是由指定范围内的满足给定条件的所有对象聚集在一 起构成,每一个对象称为这个集合的元素。
公理化集合论
  • 外延公理+空集存在公理+无序对公理+并集公理+幂集公理+无穷公理+替换公理+正则公理+选择公理。(ZFC 公理化集合论)（前八个叫ZF公理）

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QaOnVflq-1654853679749)(C:\Users\陌然\AppData\Roaming\Typora\typora-user-images\image-20220610162508934.png)]

集合的表示
枚举法

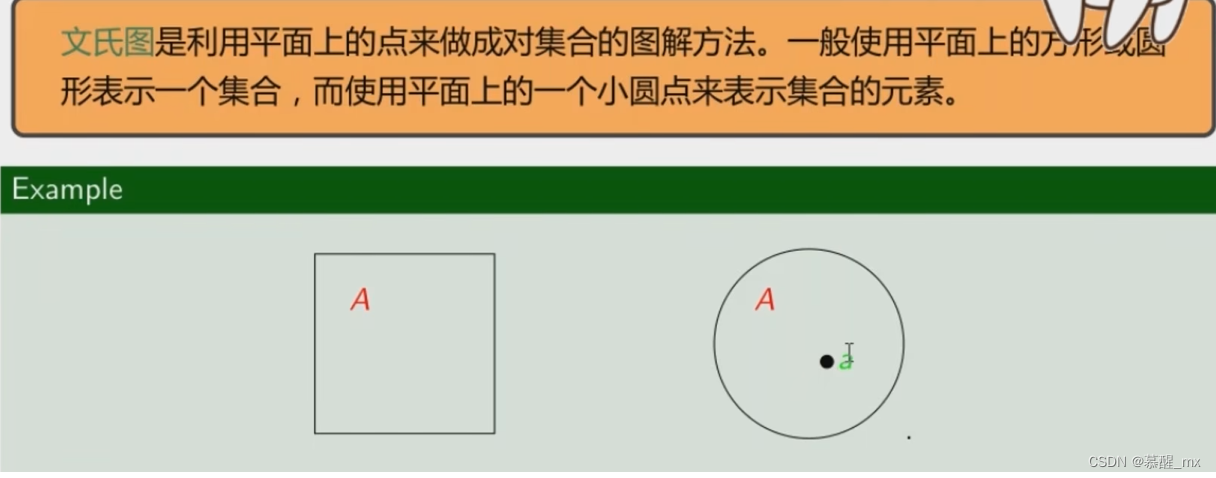
在这里插入图片描述

叙述法

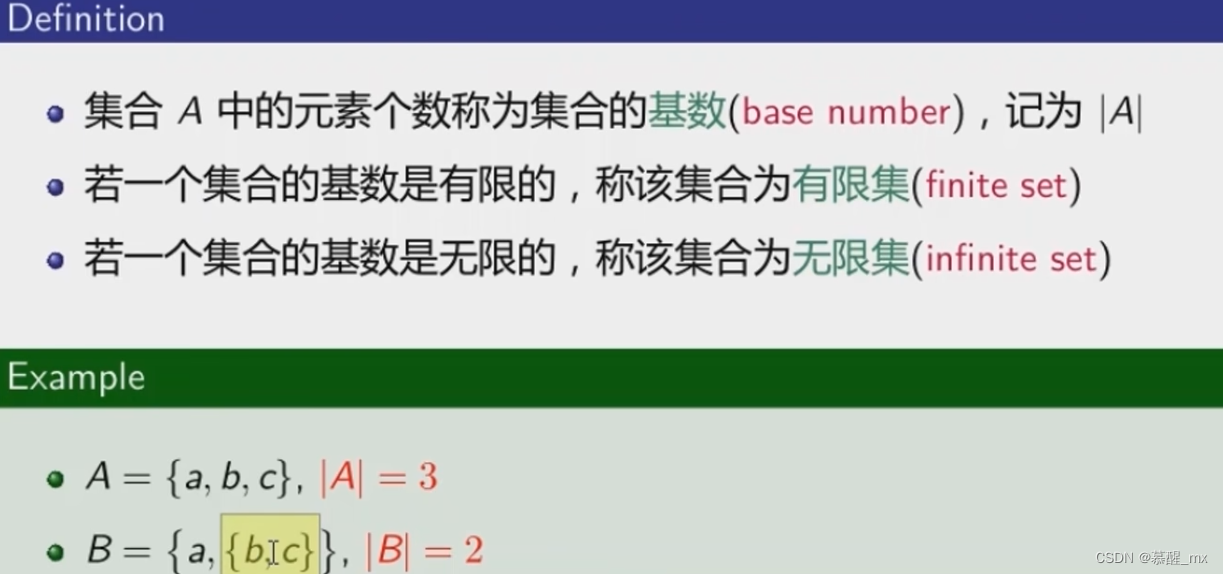
在这里插入图片描述

文恩图（文氏图）

在这里插入图片描述

集合基数

在这里插入图片描述

1.2特殊集合与集合间关系

空集
  • 空集是绝对唯一的

全集
  • 全集是相对唯一的，在某一个研究对象中全集是唯一的

在这里插入图片描述

集合的相等关系
  • 集合中相同的元素通常看成同一个元素
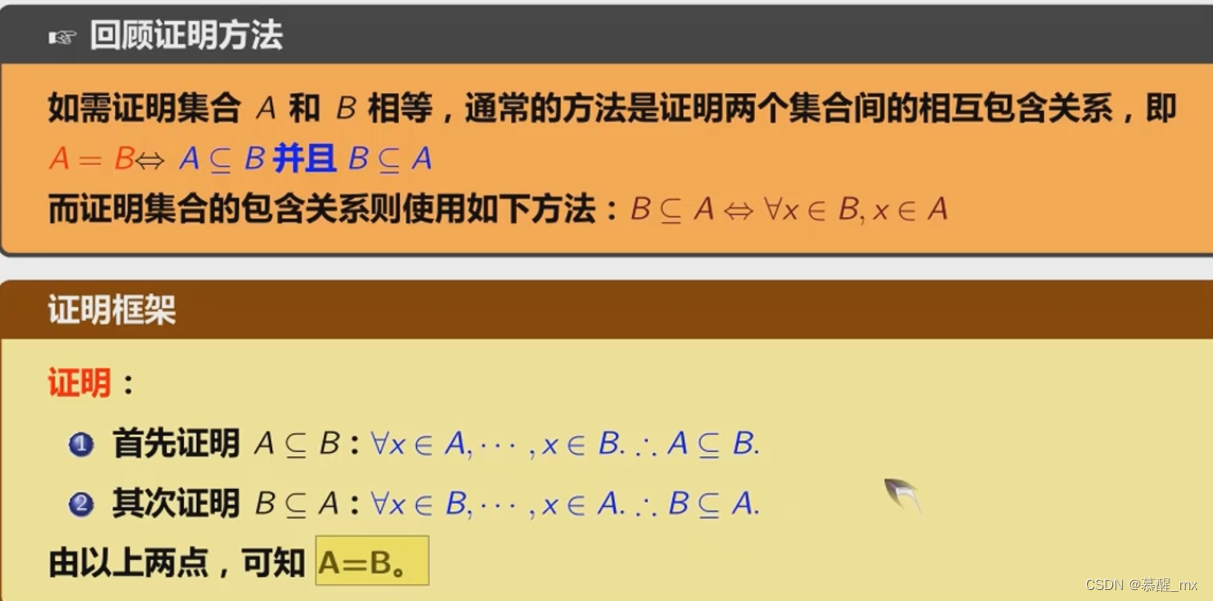
    在这里插入图片描述
子集和真子集

在这里插入图片描述

证明集合关系

在这里插入图片描述

n元素的子集

在这里插入图片描述

幂集

在这里插入图片描述

1.3集合的运算

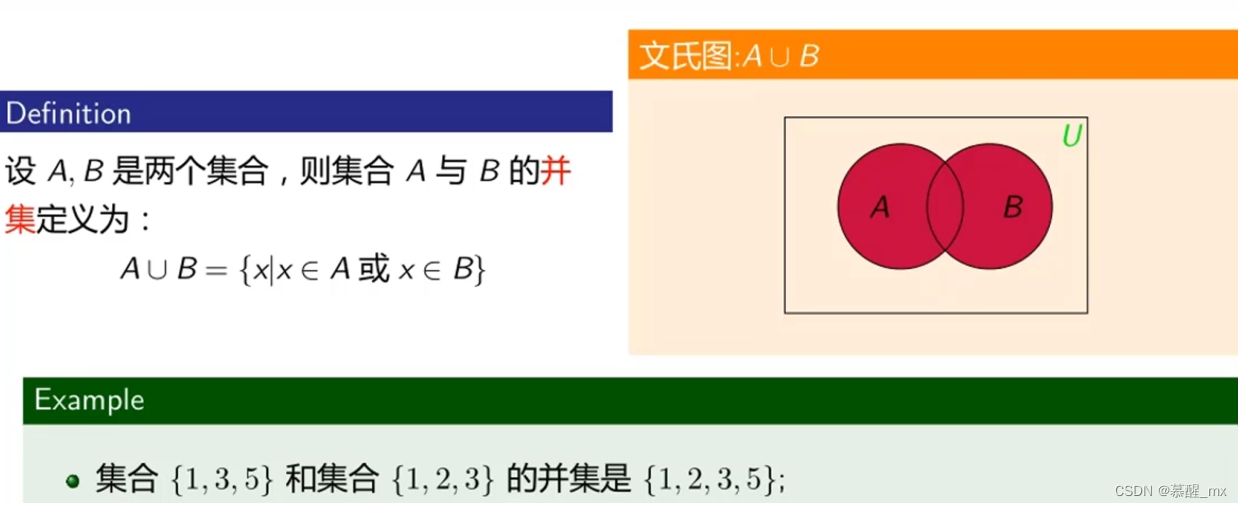
并集

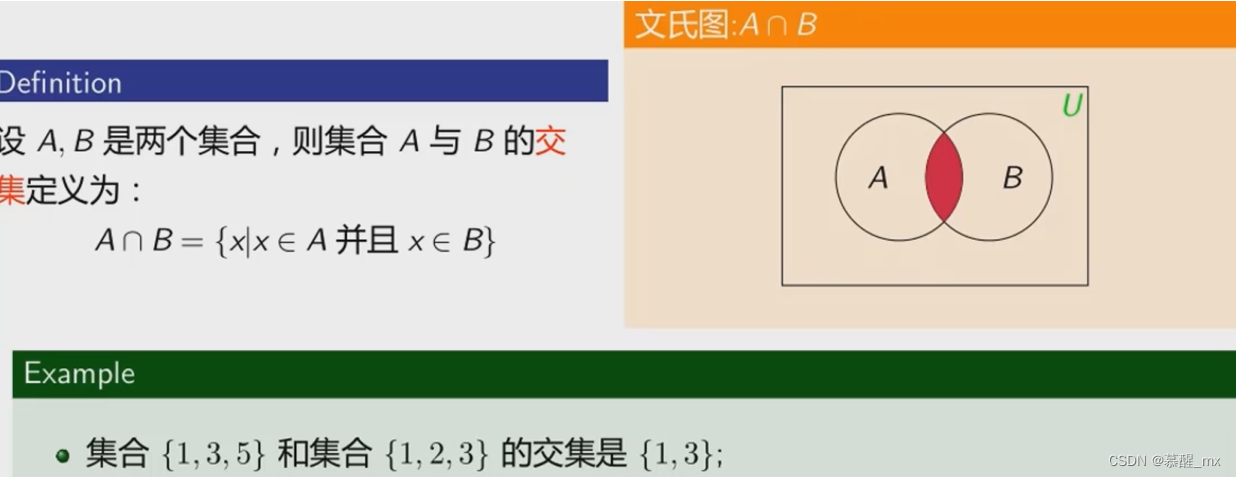
在这里插入图片描述

交集

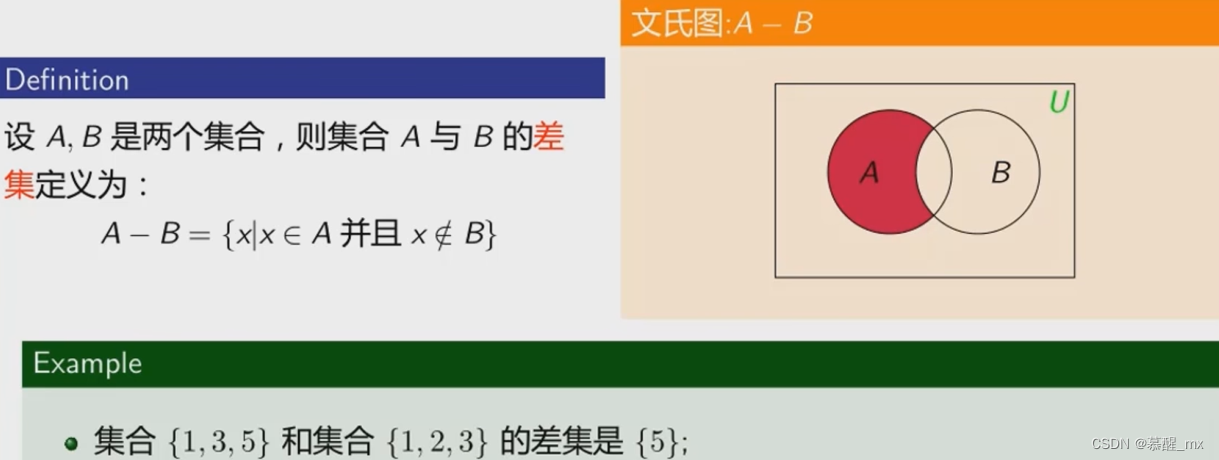
在这里插入图片描述

补集

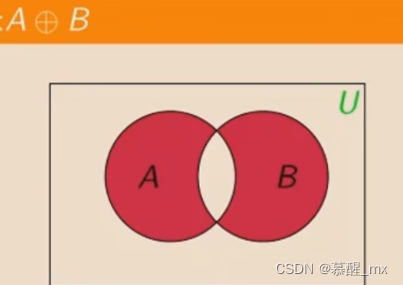
在这里插入图片描述

差集

在这里插入图片描述

对称差集

在这里插入图片描述

并集和交集的扩展

在这里插入图片描述

1.4集合的运算定律

运算定律

在这里插入图片描述

证明相等

在这里插入图片描述

1.5可数集合与不可数集合

自然数集的定义

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ijG8dBu6-1654853679761)(C:\Users\陌然\AppData\Roaming\Typora\typora-user-images\image-20220610171036665.png)]

自然数的定义

在这里插入图片描述

等势

在这里插入图片描述

可数集合

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KDlpJqc6-1654853679763)(C:\Users\陌然\AppData\Roaming\Typora\typora-user-images\image-20220610171832131.png)]

在这里插入图片描述

不可数集合

在这里插入图片描述

  • 实数包括有理数和无理数，有无理数就属于不可数了

第一章重点归纳

1.求子集

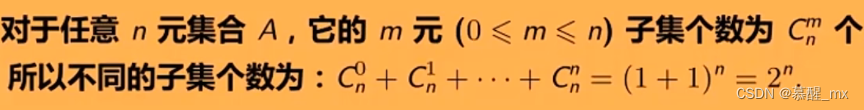
在这里插入图片描述

2.幂集

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-C4aWWLml-1654853679765)(C:\Users\陌然\AppData\Roaming\Typora\typora-user-images\image-20220610172641595.png)]

3.对称差集

在这里插入图片描述

4.等势：
  • 可以做到一一对应
5.可数集合：和N等势的集合

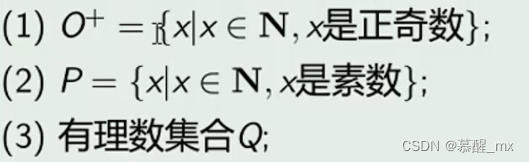
在这里插入图片描述

6.不可数集合：与开区间（0，1）等势的集合

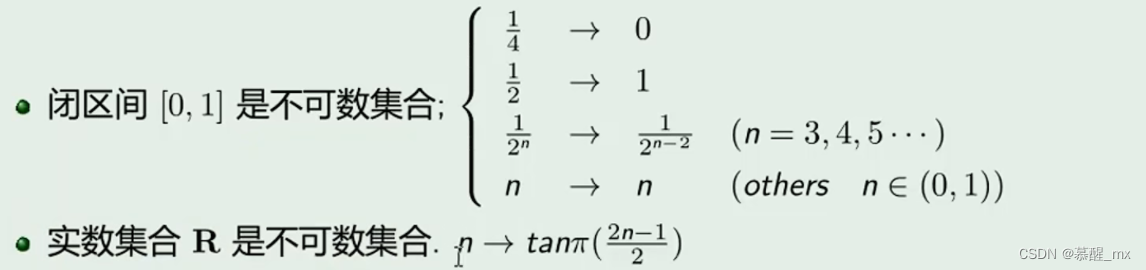
在这里插入图片描述

交集、并集、差集、对称差运算（集合类） C++实现
06-27 6626
给爷，爬到爷的收藏夹里面去吃灰去
【梳理】离散数学 第2版 第9章 代数系统 9.1 二元运算及其性质
COFACTOR
08-29 8336
9.1 二元运算及其性质 （原文档高清截图在最后，已排版） 1、设集合S，函数 f: S×S→S 称为S上的二元运算，简称二元运算。 2、2、一个运算为S上的二元运算，需要符合如下两点： （1）集合S中的任意两个元素都能运算，且结果唯一； （2）（1）中的任何运算结果都属于S，即S对该运算封闭。 例： （1）自然数集N上的加法和乘法都是N上的二元运算，而减法和除法不是。因为减法的结果可能出现零、...
集合——离散数学part 1
yun_gao_的博客
06-11 9765
集合 集合基本概念 一.集合的表示方法 二.集合的关系：相等，包含 三.特殊结合：全集，补集，幂集 ☆幂集P(A)：集合A的所有子集作为元素构成的集合称为集合A的幂集 ☆基：有限集A含有的元素个数 |A|=n,则|P(A)|=2^n 四.集合的运算 1.交和， 交换律，结合律，分配律，德摩根律 ☆2.差，对称差 ①差：A-B={x|x∈A∧x∉B} A−B=AB‾A-B=A\overline{B}A−B=AB ②对称差：A⊕B=B⊕A=（A-B）∪（B-A） A⊕B=A∪B-A∩B ☆五.证明题 在证明时，
离散数学-命题逻辑+异或(对称差)+主析取范式+主合取范式+推理
ResumeProject的博客
01-24 1万+
命题逻辑异或与精确表达异或精确表达:真值表需要精确对应命题公式的简化与命题等价命题公式的简化命题等价:真值表相同基础等价公式重言式(永真式)与矛盾式(永假式)重言蕴含式：基础重言蕴含式范式析取范式与合取范式主析取范式和主合取范式推理推理的方法推理的规则 异或与精确表达 异或 异或，英文为exclusive OR，缩写成xor 异或的数学符号为“⊕”，计算机符号为“eor”。其运算法则为： a⊕b = (¬a ∧ b) ∨ (a ∧¬b) 如果a、b两个值不相同，则异或结果为1。如果a、b两个值相同，异或结果
离散数学 集合论初步
skn000的博客
02-09 1307
集合论总结 关系 **元素与集合的关系：**属于与不属于 **集合与集合的关系：**相等、包含与不包含 运算 交运算、并运算、相对补与绝对补、对称差。 相对补与绝对补： A−BA-BA−B 与 E−B（∼B)E-B（\sim B)E−B（∼B) 对称差： (A−B)∪(B−A)(A-B)\cup(B-A)(A−B)∪(B−A) 包含排斥原理 跟概率中的部分知识重合，比较简单。 两个集合时： ∣A∪...
离散数学-集合的简单运算【并、交、差、补、环合（对称差）】
热门推荐
Snikai1的博客
08-14 2万+
关于集合的并交差 1.集合的常用运算： 并集：X∪Y={x | x∈X或x∈Y}。 交集：X∩Y={x | x∈X且x∈Y}。 差集：X-Y={x | x∈X且x∉Y}。 如果X∩Y=∅，那么集合X与Y不相交。如果集合X和Y是集族S中的不同集合且X和Y不相交，那么集族S两两不相交。 #include <stdio.h> #define N 100 main() { int a[N],b[N],c[N],d[N],e[N],h[N]; int aa[N],bb[.
3.2集合的运算
m0_51343122的博客
04-22 505
此专题用于离散数学的复习，基本概念+课堂ppt节选+自我理解，持续更新中······欢迎批评指正！ 目录 离散数学 第三章 集合与关系 3.2 集合的运算 一.交 二.并 三.补 四.对称差 一.交 A和B是集合，由所以既属于A又属于B的元素组成的集合S，称为A和B的交集，记作A∩B=S。 注意集合∩与数理逻辑中的合取运算不同。 二.并 A和B是集合，由所有属于A或者属于B的元素组成的集合S，称为A和B的并集，记作A∪B=S。 同理，与析取运算不同。 交与并之间.
离散数学第一章
03-06
离散数学第一章
离散数学 第一章
08-10
第1章集合映射运算.ppt
南京邮电大学离散数学第一章实验的MATLAB代码
最新发布
04-03
南京邮电大学离散数学第一章实验的MATLAB代码涉及离散数学这一数学分支的基础知识与编程实践相结合的内容。离散数学作为计算机科学与数学交叉领域的重要基础，其核心包括了图论、逻辑、集合、关系、函数以及基本的...
离散数学第一章predicate记录
10-20
离散数学第一章predicate记录
离散数学-6 集合代数
哈哈岛
03-15 6815
1. 集合定义 集合没有精确的数学定义 理解：由离散个体构成的整体称为集合，称这些个体为集合的元素 常见的数集：N, Z, Q, R, C 等分别表示自然数、整数、有理数、实数、复数集合 2. 集合表示法 枚举法----通过列出全体元素来表示集合 谓词表示法----通过谓词概括集合元素的性质 实例：
集合的异或运算（对称差）
weixin_30876945的博客
12-06 8990
1、集合的异或运算(AΔB)定义属于A或属于B，但不同时属于A和B的元素的集合称为A和B的对称差，即A和B的异或。 注：草绿色部分即为 AΔB 2、对称差(异或)运算的定律2.1 AΔB = (A-B)∪(B-A) = (A∪B)-(A∩B)该公式的证明已在 集合的证明及相关习题 中证明了 2.2 对称差运算的交换律(AΔB)ΔC = (AΔC)ΔB 注：图1中草绿色部分为 (A...
# 离散数学#对称和反对称
applause_1的博客
12-31 1万+
亦你“具有对称性的关系”。对于类k中一个确定的关系R来说，类k中的任意两个个体x，y， 如果xRy真yRx就必真，则称关系R为类k中对称的关系（对称关系）， 如果xRy真yRx就必假， 则称关系R为类K中反对称的关系（反对称关系）；如果对于某些个体x，y， xRy真同时yRx也真， 而对于另外的个体x，y，xRy真时yRx却假，则称关系R为类k中非对称的关系（非对称关系）。例如，两条直线之间的平行关系、垂直关系、 两个数之间的相等关系等都是对称的关系；两个实数之间的大于关系、 小于关系等部是反对称的关系，两
两个集合的并、交，相对补，对称差的运算
weixin_40562633的博客
01-04 7005
/*编写程序实现两个集合的并、交，相对补，对称差的运算并判断两个集合是否相等? （2）功能要求 ①输入集合A与集合B的元素。 ②输出集合A与B的并、交、相对补、差、对称差运算。 ③输出集合A与B是否相等的断定结果。 ④输出集合A与B的幂集。*/ #include "stdio.h" int disc; void xd(int a[],int b[],int n,int m) {
离散数学归总
松子茶的专栏
04-16 9673
离散数学是现代数学的一个重要分支，计算机科学与技术一级学科的核心课程，是整个计算机学科的专业基础课。离散数学是以研究离散量的结构和相互间的关系为主要目标，其研究对象一般地是有限个或可数个元素，因此它充分描述了计算机科学离散性的特点。离散数学是随着计算机科学的发展而逐步建立的，它形成于七十年代初期，是一门新兴的工具性学科。关于Discrete Mathematics更多讨论与交流，敬请关注本博客和新浪微博songzi_tea.
离散数学拾趣（三）：集合的子集有多少个
weixin_33961829的博客
03-10 733
集合广泛应用于计数问题，这类问题需要讨论集合的大小。 令S为集合。若S中恰有n个不同的元素，n是非负整数，就说S是有限集合，而n是S的基数，用|S|表示。若S={ 1, 2, 3 }，则|S| = 3。 有时候需要考虑一个集合的元素所有可能的组合，看它们是否具有某种性质。为此构造一个新的集合，它以S的所有子集作为它的元素，该集合称为S的幂集合，记为P(S)。 比如： 本文的主题也就是：对于...
离散数学 8.1.2子集（C语言）
extern_int_Lin的博客
02-25 2729
[问题描述] 给定一个集合A，求A的所有非空子集。例如A={a,b}时，则它的所有非空子集为{a},{b},{a,b}。集合A不空，并且A的元素个数不超过10个。 [输入] 有多组测试数据，每组测试数据为一行。 每行表示一个集合，集合由一对大括号括起来，集合之间的元素用一个逗号隔开。之间没有任何的空白字符。已经知道集合元素按字典顺序排列。 [输出] 每组测试数据输出为2^n-1...
离散数学笔记
Wowlittlemoon的博客
12-09 1万+
1. 命题逻辑 2. 一阶逻辑 3. 集合论 3.1 集合代数 3.2 二元关系 3.3 函数 4. 图论 4.1 图的基本概念 4.2 通路和回路 4.3 图的矩阵表示 4.4 欧拉图&哈密顿图 5. 树 5.1 无向树 5.2 生成树
离散数学第一章证明字母
01-02
离散数学的第一章通常会介绍基本概念，包括逻辑运算符、命题及其连接词（如合取、析取、条件和双条件）、真值表以及如何构造和分析论证。当提到"字母"时，在这个上下文中指的是代表命题的符号或者变量，比如$p, q, r$等。 对于涉及这些表示命题的字母的证明，一般是指使用形式化的规则来验证某个给定陈述的有效性。这可能涉及到： - 命题演算的基本定律的应用，例如德·摩根律、分配律、结合律等等。 - 构造真值表以展示一个特定的命题组合总是为真（即是一个重言式），或是为了确定两个命题是否等价。 - 应用推理规则，像分离规则（modus ponens）或其他演绎法则来进行推导。 由于具体的证明内容依赖于所使用的教材及具体题目要求，下面提供一些通用的方法用于处理这类问题： 可以尝试简化复杂的命题公式至更简单但保持原意的形式。利用已知的逻辑恒等式替换复杂表达式的部分，直到整个表达式变得足够直观理解为止。 针对需要证明两命题等价的情况，可以通过构建两者之间的双向蕴含链路完成。这意味着不仅要从左向右证明成立，也要反过来证实另一方向同样有效。 在面对较为抽象的问题时，考虑采用反证法。假设结论相反的情形是真的，接着逐步推出矛盾点从而否定最初的假定，以此确认原来想要证明的结果确实正确无误。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值