Option-Critic架构以其优雅的端到端训练框架,使得任务的子目标可以直接由网络学习,无需进行人为设计。然而其代价便是高层策略输出的目标沦为了训练过程中难以捉摸的黑箱变量,我们只能依赖外部奖励引导整个网络的训练,无法进一步对高层策略和底层策略进行区别干预。FeUdal Networks则为目标赋予了一个更清晰的语义,在保留端到端架构的前提下,通过精巧的机制实现了高层策略和底层策略的分离学习。
FeUdal Networks
FeUdal Networks(封建网络,简称FuN)是一个模块化神经网络,包括工人Worker和管理者Manager两个模块。管理者负责高层决策,向工人输出目标;工人负责底层执行,结合管理者的目标输出动作。
管理者-工人架构
FuN的网络架构与此前介绍的算法有显著区别,主要在于
- 管理者拥有自己的状态空间转换网络,用于从环境中提取出有别于工人的、用于长期战略规划的抽象状态作为输出目标的依据;
- 管理者和工人的策略网络采用循环神经网络(RNN)。RNN在每个时间步接收当前观测和网络上一时间步的记忆作为输入,输出新的记忆和决策结果。RNN使得智能体能够利用从过去到现在所有观测的历史信息来进行决策,推断那些无法从当前状态直接看到的信息,例如玩扑克牌需要记住之前出过的牌来推断对手可能的手牌;
- 管理者决策的时间步间隔是固定的,而非等待子目标终止后决策。在基于目标终止条件的高层决策中,终止条件的学习带来了更大的训练难度,并让信用分配更加复杂。FuN通过固定决策间隔,以牺牲目标的灵活性为代价换来了更稳定的训练,并且让高层可以给予底层持续的引导,防止底层在错误的方向上走得太远;
- 工人并非直接根据当前状态和目标给出动作,而是先依赖当前状态输出一个中间矩阵,再与目标结合给出动作。这个过程将问题进一步分解,即工人不需要直接学习从状态-目标对到动作的复杂映射,而是可以被理解为只学习某个状态下的行动空间,包含所有可能的行动方案,目标则作为权重再对这些行动方案进一步筛选得到最终的动作。这种解耦可以引导模型学习一种结构化的策略空间,相比直接学习从状态-目标对到动作的复杂函数更加简单且易于优化。
现在我们来详细展开FuN中前向传播的每一步:
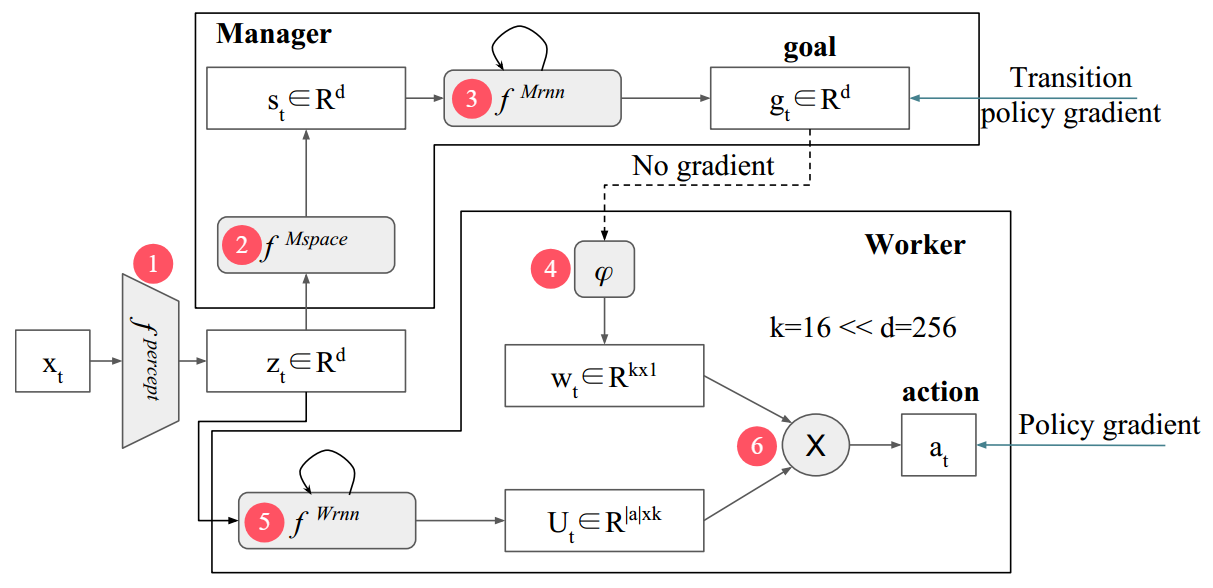
①环境感知网络fperceptf^{percept}fpercept(可选),用于从复杂高维的原始环境信息xtx_txt中提取特征表示ztz_tzt:
zt=fpercept(xt) z_t=f^{percept}(x_t) zt=fpercept(xt)
论文中使用卷积神经网络处理像素图像。如果环境可以由人工设计的低维状态空间表示,则这一步可以省略。
②管理者状态空间转换网络fMspacef^{Mspace}fMspace,用于从特征ztz_tzt进一步提取出更高层的潜在状态sts_tst:
st=fMspace(zt) s_t=f^{Mspace}(z_t) st=fMspace(zt)
③管理者RNNfMrnnf^{Mrnn}fMrnn,根据潜在状态sts_tst制定当前的目标gtg_tgt:
htM,g^t=fMrnn(st,ht−1M)gt=g^t∥g^t∥ \begin{split} &h_t^M,\hat g_t=f^{Mrnn}(s_t,h_{t-1}^M)\\ &g_t=\frac{\hat g_t}{\|\hat g_t\|} \end{split} htM,g^t=fMrnn(st,ht−1M)gt=∥g^t∥g^t
其中ht−1Mh_{t-1}^Mht−1M和htMh_t^MhtM分别为管理者RNN上一个时间步和当前时间步的隐藏状态,g^t\hat g_tg^t为管理者输出的原始目标向量。最终的目标向量gtg_tgt由g^t\hat g_tg^t归一化得到,从而让管理者只关心目标的方向而不关心大小。
④目标嵌入ϕ\phiϕ,用于将目标转化为工人能理解的指令(作用方式见⑥):
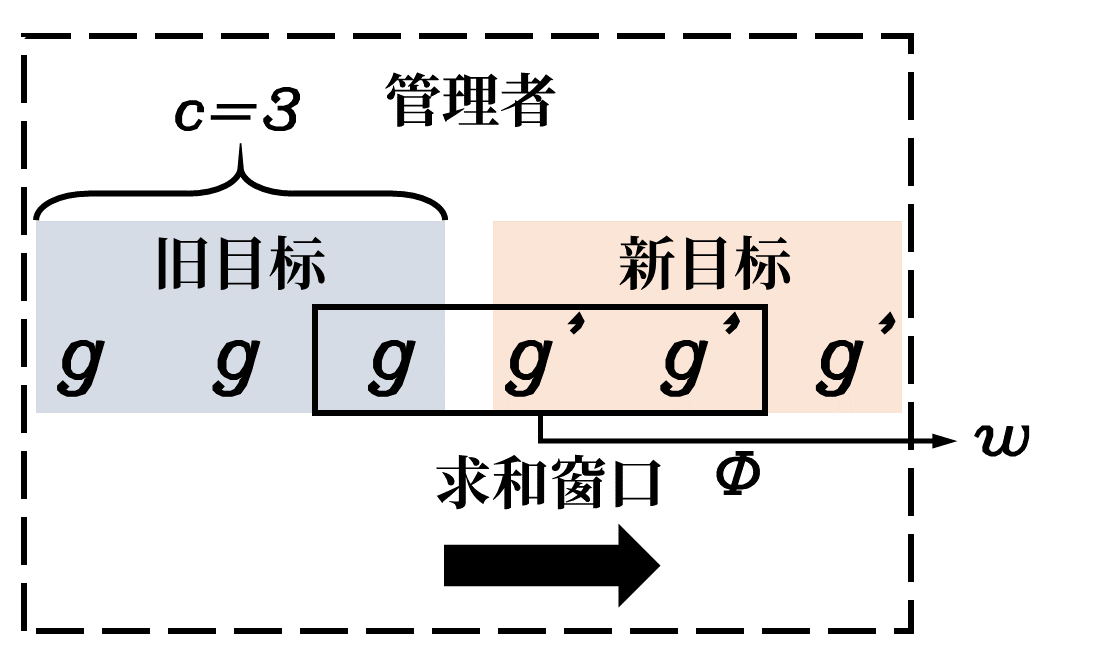
wt=ϕ(∑i=t−ctgi) w_t=\phi(\sum^t_{i=t-c}g_i) wt=ϕ(i=t−c∑tgi)
其中ϕ\phiϕ是一个线性转换层,wtw_twt是嵌入后的目标向量。求和操作可以平滑管理者每隔ccc个时间步给出新目标时的目标跳变。如果在工人按照旧目标执行ccc步后突然切换为新目标,会带来训练不稳定和智能体行为不连贯的问题。目标嵌入通过对一定时间步范围内的目标求和,可以平缓地从旧目标过渡到新目标。自管理者给出新目标后,新目标的权重会随着时间推移越来越大。
⑤工人RNNfWrnnf^{Wrnn}fWrnn,根据特征ztz_tzt输出一个矩阵UtU_tUt:
htW,Ut=fWrnn(zt,ht−1W) h_t^W,U_t=f^{Wrnn}(z_t,h_{t-1}^W) htW,Ut=fWrnn(zt,ht−1W)
UtU_tUt被设计为工人根据当前状态列出的kkk个行为模式,每个行为模式包含对所有动作的偏好值,可以理解为未经归一化处理的策略概率分布。UtU_tUt大小为∣a∣×k|a|\times k∣a∣×k,∣a∣|a|∣a∣为动作数量。
⑥最终策略πt\pi_tπt,由工人的输出矩阵UtU_tUt和管理者的目标嵌入wtw_twt相乘后进行softmax操作得到:
πt=SoftMax(Utwt) \pi_t=SoftMax(U_tw_t) πt=SoftMax(Utwt)
wtw_twt大小为k×1k\times1k×1,通过与UtU_tUt相乘对所有的行为模式进行加权求和得到最终的行为模式,softmax操作将其转化为所有动作的概率分布。
管理者策略梯度
整个FuN架构是可微分的,理论上可以用策略梯度算法进行纯粹的端到端训练。但是如果只通过工人执行的动作产生的梯度来反向传播训练管理者,那么目标gtg_tgt就会沦为一个黑箱中的内部信号,可能无法学习到我们期望的“目标”的语义。为此,FuN赋予了目标“状态转移的方向”这一内涵,设计了一个独立的训练信号来训练管理者预测状态空间中“有利的方向”作为目标向量的方向,其更新规则如下
∇gt=AtM∇θMdcos(st+c−st,gt(θM)) \nabla g_t=A_t^M\nabla_{\theta^M}d_{\cos}(s_{t+c}-s_t,g_t(\theta^M)) ∇gt=AtM∇θMdcos(st+c−st,gt(θM))
- AtM=Rt−VtM(xt,θ1)A_t^M=R_t-V_t^M(x_t,\theta_1)AtM=Rt−VtM(xt,θ1):管理者的优势函数,用于衡量在状态xtx_txt下,遵循当前管理策略的好坏程度。其中:
- RtR_tRt:从时刻ttt开始的累积奖励;
- VtM(xt,θVM)V_t^M(x_t,\theta^{V_M})VtM(xt,θVM):管理者评论家网络对状态xtx_txt的价值估计,θVM\theta^{V_M}θVM为网络参数。
- dcos(α,β)=αTβ/(∣α∣∣β∣)d_{\cos}(\alpha,\beta)=\alpha^T\beta/(|\alpha||\beta|)dcos(α,β)=αTβ/(∣α∣∣β∣):余弦相似度,用于衡量向量α\alphaα与β\betaβ的方向有多接近,在式中的参数为:
- st+c−sts_{t+c}-s_tst+c−st:在潜在状态空间中,从当前时刻ttt到未来ccc步后的实际状态变化量;
- gt(θM)g_t(\theta^M)gt(θM):管理者在时刻ttt预测的、希望工人实现的目标方向。管理者参数θM\theta^MθM是从xtx_txt到gtg_tgt所经历的所有网络的参数,包括感知器参数θpercept\theta^{percept}θpercept、管理者状态空间转换网络参数θMspace\theta^{Mspace}θMspace和管理者RNN参数θMrnn\theta^{Mrnn}θMrnn。该更新规则不考虑梯度对潜在状态sss的依赖,因此主要对θMrnn\theta^{Mrnn}θMrnn起更新作用。
总而言之,管理者的更新规则是一个双目标优化过程:优势函数AtMA_t^MAtM让目标沿着能带来更高回报的方向更新,而余弦相似度梯度∇θMdcos(st+c−st,gt(θM))\nabla_{\theta^M}d_{\cos}(s_{t+c}-s_t,g_t(\theta^M))∇θMdcos(st+c−st,gt(θM))保证管理者给出的目标gtg_tgt能够准确地指导工人的行为,进而牵引状态转移。二者共同作用让目标的更新有利且有效。
管理者将在每一个决策点之前,即一个目标周期结束时更新参数,以确保其更新所用序列均基于计算梯度所用的目标。
工人策略梯度
FuN为工人设置了一个内在奖励作为其更新目标之一
rtI=1c∑i=1cdcos(st−st−i,gt−i) r_t^I=\frac1c\sum^c_{i=1}d_{\cos}(s_t-s_{t-i},g_{t-i}) rtI=c1i=1∑cdcos(st−st−i,gt−i)
该内在奖励是对过去ccc步,也就是每个目标的作用时间内,状态转移和目标的余弦相似度的平均。具体而言,其衡量的是对于管理者在t−it-it−i时刻给出的目标gt−ig_{t-i}gt−i,工人在经过iii步后,产生的状态转移与之有多一致。与此前介绍的算法相比,FuN不要求工人到达某个特定状态,而是奖励它朝着正确的方向改变状态,进而鼓励了持续的目标导向的探索。
工人的内在奖励和管理者的更新规则都涉及状态转移和目标的余弦相似度,这体现了一种对称性。管理员调整目标确保其被正确传达给工人,而工人则调整策略确保能正确执行管理者的目标,最终达成高层决策与底层执行的相统一。
FuN的又一创新举措是采用混合奖励信号训练工人,让工人不仅通过内部奖励服从管理者的目标,也要看到外部奖励以理解任务的终极目标来微调行为。工人的总奖励是外部奖励和内部奖励的加权和
RtD=Rt+αRtI R^D_t=R_t+\alpha R^I_t RtD=Rt+αRtI
其中RtR_tRt为累积外部奖励,RtIR_t^IRtI为累积内部奖励,超参数α\alphaα用于平衡两种奖励的重要性。
工人参数θW\theta^WθW,包括感知器参数θpercept\theta^{percept}θpercept、工人RNN参数θWrnn\theta^{Wrnn}θWrnn和目标嵌入层参数θϕ\theta^\phiθϕ的更新基于A2C算法,即采用优势策略梯度作为更新规则
∇πt=AtD∇θWlogπ(at∣xt;θW) \nabla\pi_t=A_t^D\nabla_{\theta^W}\log\pi(a_t|x_t;\theta^W) ∇πt=AtD∇θWlogπ(at∣xt;θW)
其中工人的优势函数AtDA^D_tAtD定义为
AtD=RtD−VtD(xt;θVW) A^D_t=R^D_t-V_t^D(x_t;\theta^{V_W}) AtD=RtD−VtD(xt;θVW)
VtD(xt;θVW)V_t^D(x_t;\theta^{V_W})VtD(xt;θVW)是工人评论家网络,其参数为θVW\theta^{V_W}θVW。
工人和管理者在计算累积奖励时可以采用不同的折扣因子γ\gammaγ,让工人更短视以专注眼前的回报,而管理者则考虑长期回报。
转移策略梯度
FuN提出了转移策略,进一步给出了管理者和工人采用上述策略梯度的理论基础。我们记管理者策略为gt=μ(st,θM)g_t=\mu(s_t,\theta^M)gt=μ(st,θM),而工人的行为对管理者体现为一个状态转移分布p(st+c∣st,gt)p(s_{t+c}|s_t,g_t)p(st+c∣st,gt),这个分布描述了在状态sts_tst下,如果管理者给出了目标gtg_tgt,那么经过ccc步后状态st+cs_{t+c}st+c的概率分布是怎样的。将管理者策略和这个状态转移分布结合,可以定义一个新的策略
πTP(st+c∣st)=p(st+c∣st,μ(st,θM)) \pi^{TP}(s_{t+c}|s_t)=p(s_{t+c}|s_t,\mu(s_t,\theta^M)) πTP(st+c∣st)=p(st+c∣st,μ(st,θM))
该策略即为转移策略,它输出的不是动作,而是ccc步后的状态分布。在原始的MDP上学习管理者策略,等价于在一个新的MDP上学习这个转移策略,其中新MDP的每一步对应原始MDP中的ccc步。因此转移策略是一个有效的策略,可以应用策略梯度定理。
博主的理解是,原始策略π(a∣s)\pi(a|s)π(a∣s)输出的动作分布本质上也和环境的动态特性p(s′∣s,a)p(s'|s,a)p(s′∣s,a)共同决定了一个状态转移分布
pπ(s′∣s)=∑aπ(a∣s)p(s′∣s,a) p_\pi(s'|s)=\sum_a\pi(a|s)p(s'|s,a) pπ(s′∣s)=a∑π(a∣s)p(s′∣s,a)
而在转移策略中,这个逻辑被反转了。转移策略输出的状态转移分布,实际上也隐式地指向了一个动作序列的分布(a0,a1,⋯ ,ac−1)(a_0,a_1,\cdots,a_{c-1})(a0,a1,⋯,ac−1)。这个指向关系难以由计算得到,因此在FuN中,它成为了工人的学习任务,也就是学习如何在ccc步内采取一系列动作以实现管理者期望的状态转移分布,而管理者只需从宏观的状态转移视角作出决策。换言之,管理者不会告诉工人“怎么做”,只会要求“实现什么目标”。
显然,转移策略的策略梯度定理是有条件的,它要求工人有能力满足管理者的要求,能以管理者给出的目标为中心落实状态转移。从数学上来讲,即对于当前状态sts_tst和管理者给出的目标gtg_tgt,在工人ccc步后可达的状态集合中,存在一些状态st+cs_{t+c}st+c能够符合转移策略给出的分布p(st+c∣st,gt)p(s_{t+c}|s_t,g_t)p(st+c∣st,gt)。
FuN选择VMF分布作为转移策略πTP(st+c∣st)\pi^{TP}(s_{t+c}|s_t)πTP(st+c∣st)输出的分布
p(st+c∣st,gt)∝edcos(st+c−st,gt) p(s_{t+c}|s_t,g_t)\propto e^{d_{\cos}(s_{t+c}-s_t,g_t)} p(st+c∣st,gt)∝edcos(st+c−st,gt)
我们可以将其理解为球面上的高斯分布,正如我们令一个原始策略π(a∣s)\pi(a|s)π(a∣s)以高斯分布作为输出一样。采用球面是因为我们关注的是状态转移的方向。在该分布下,转移策略的策略梯度形式将符合管理者参数的更新规则
∇gt=AtM∇θMdcos(st+c−st,gt(θM)) \nabla g_t=A_t^M\nabla_{\theta^M}d_{\cos}(s_{t+c}-s_t,g_t(\theta^M)) ∇gt=AtM∇θMdcos(st+c−st,gt(θM))
实际上FuN正是基于该转移策略对管理者的更新规则进行推导的,而工人的内部奖励函数的设计也是为了满足转移策略能应用于策略梯度定理的条件。
算法流程
我们将感知器和管理者状态空间转换网络统一记为编码器fencoder(xt;θenc)f^{encoder}(x_t;\theta^{enc})fencoder(xt;θenc),负责将xtx_txt编码为ztz_tzt和sts_tst,其参数将通过工人和管理者的梯度留进行更新。
最终我们给出FuN的一个算法伪代码如下:
(原论文没有给出伪代码,博主自行给出,仅供参考)
- 初始化:
- 管理者策略网络μ(st;θM)\mu(s_t;\theta^M)μ(st;θM)及其评论家VtM(xt,θVM)V_t^M(x_t,\theta^{V_M})VtM(xt,θVM);
- 工人策略网络π(at∣zt,wt;θW)\pi(a_t|z_t,w_t;\theta^W)π(at∣zt,wt;θW)及其评论家VW(xt;θVW)V^W(x_t;\theta^{V_W})VW(xt;θVW);
- 编码器fencoder(xt;θenc)f^{encoder}(x_t;\theta^{enc})fencoder(xt;θenc);
- 目标嵌入层ϕ\phiϕ;
- 管理器时间尺度ccc,折扣因子γM,γW\gamma^M,\gamma^WγM,γW,内部奖励权重α\alphaα;
- 经验存放缓存区D\mathcal DD(用于更新管理者参数)。
- 对每一幕循环:
- 初始化观测x←x0x\leftarrow x_0x←x0;
- 编码初始状态z,s←fencoder(x)z,s\leftarrow f^{encoder}(x)z,s←fencoder(x);
- 初始化管理者和工人的隐藏状态hM←h0Mh^M\leftarrow h^M_0hM←h0M,hW←h0Wh^W\leftarrow h^W_0hW←h0W;
- 初始化目标队列GGG;
- 对每一个时间步循环:
- 如果t%c=0t\%c=0t%c=0:
- 管理者决策g,hM←μ(s,hM;θM)g,h^M\leftarrow\mu(s,h^M;\theta^M)g,hM←μ(s,hM;θM);
- 将ggg加入队列GGG,并保持队列长度为ccc(移除旧目标);
- 目标嵌入w←ϕ(∑g∈Gg)w\leftarrow\phi(\sum_{g\in G}g)w←ϕ(∑g∈Gg);
- 生成最终策略π,hW←π(z,w,hW;θW)\pi,h^W\leftarrow\pi(z,w,h^W;\theta^W)π,hW←π(z,w,hW;θW);
- 根据π\piπ采样动作aaa;
- 执行动作aaa,观测奖励rrr和后继状态x′x'x′;
- 编码后继状态z′,s′←fencoder(x′)z',s'\leftarrow f^{encoder}(x')z′,s′←fencoder(x′);
- 将(x,a,r,x′)(x,a,r,x')(x,a,r,x′)存入缓存区D\mathcal DD;
- 更新工人策略参数θW\theta^WθW;
- 更新工人评论家参数θVW\theta^{V_W}θVW;
- 如果t+1%c=0t+1\%c=0t+1%c=0:
- 更新管理者策略参数θM\theta^MθM;
- 更新管理者评论家参数θVM\theta^{V_M}θVM;
- 如果t%c=0t\%c=0t%c=0:





















 1631
1631

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








