广度优先搜索（广搜）4（c++）

原创于 2025-02-13 15:00:08 发布 · 815 阅读

22 ·

CC 4.0 BY-SA版权

文章标签：

#宽度优先 #c++

Dungeon Master

题目描述

这题是一个三维的迷宫题目，其中用‘.’表示空地，‘#’表示障碍物，‘S’表示起点，‘E’表示终点，

求从起点到终点的最小移动次数，解法和二维的类似，只是在行动时除了东南西北移动外还多了上下。

可以上下左右前后移动，每次都只能移到相邻的空位，每次需要花费一分钟，求从起点到终点最少要多久。

输入格式

多组测试数据。

一组测试测试数据表示一个三维迷宫：

前三个数，分别表示层数、一个面的长和宽，后面是每层的平面图。前三个数据为三个零表示结束。

输出格式

最小移动次数。

样例

样例输入

3 4 5 S.... .###. .##.. ###.# ##### ##### ##.## ##... ##### ##### #.### ####E 1 3 3 S## #E# ### 0 0 0

样例输出
Escaped in 11 minute(s).

Trapped!

样例解释

对于题目给出数据的含义就是输入l，r，c，分别代表迷宫有l层，每层长宽分别是c，r。对于数据以可以这样移动:

(1,1,1)->(1,1,2)->(1,1,3)->(1,1,4)->(1,1,5)->(1,2,5)->

(1,3,5)->(1,3,4)->(1,4,4)->(2,4,4)->(2,4,5)->(3,4,,5)

共11步就可以到达终点对于数据二明显不能到达，则输出Trapped！

这题用BFS解，每次去队首元素，如果是终点则输出结果移动的次数，否则，从该点开始分别向东南西北上下移动（如果可以走的话）并继续搜，如果到队列为空还没搜到解法，则说明无解。

#include <bits/stdc++.h>
using namespace std;
struct point
{
	int x,y,z,v;
	point(){};
	point(int a,int b,int c,int d)
	{
		x = a;
		y = b;
		z = c;
		v = d;
	}
};
point que[1000010];
char a[110][110][110];
int b[110][110][110];
int head;
int tail;
int n,m,h;
int cnt;
int sx,sy,sz,ex,ey,ez;
int dx[] = {0,1,0,-1,0,0};
int dy[] = {1,0,-1,0,0,0};
int dz[] = {0,0,0,0,-1,1};

void print();

int main()
{
	
	
	cin>>h>>n>>m;
	while(h!=0||n!=0||m!=0)
	{
		
		cnt = 0;
		head = 0;
		tail = 0;
		for(int i = 1;i<=h;i++)
		{
			for(int j = 1;j<=n;j++)
			{
				for(int k = 1;k<=m;k++)
				{
					cin>>a[i][j][k];
					b[i][j][k] = 0;
					b[i+1][j][k] = 0;
					a[i+1][j][k] = '#';
					if(i==1) a[i-1][j][k] = '#';
					if(a[i][j][k]=='S') sx = j,sy=k,sz=i;
					if(a[i][j][k]=='E') ex = j,ey=k,ez=i;
				}
			}
		}
		b[sz][sx][sy] = 1;
		
		
		bool t = false;
		que[++tail] = {sx,sy,sz,0};
		while(head<tail)
		{
			head++;
			for(int i = 0;i<6;i++)
			{
				int tx = que[head].x+dx[i];
				int ty = que[head].y+dy[i];
				int tz = que[head].z+dz[i];
				if(tx>=1&&tx<=n&&ty>1&&ty<=m&&tz>=1&&tz<=h&&a[tz][tx][ty]!='#'&&b[tz][tx][ty]==0)
				{
					que[++tail] = {tx,ty,tz,que[head].v+1};
					b[tz][tx][ty] = que[tail].v;
					if(tz==ez&&tx==ex&&ty==ey)
					{
						t = true;
						break;
					}
				}
			}
			if(t==true) break;
		}
		if(t==false) cout<<"Trapped!"<<endl;
		else
		{
			cout<<"Escaped in "<<b[ez][ex][ey]<<" minute(s)."<<endl;
		}
		
		cin>>h>>n>>m;
	}
	
	return 0;
}

城堡The Castle

题目描述

一座城堡被分成m*n个方块(m<50，n<50)，每个方块可有0~4堵墙(0表示无墙)。图中的加粗黑线代表墙。几个连通的方块组成房间，房间与房间之间一定是用黑线(墙)隔开的。现在要求你编一个程序，解决以下2个问题:1、该城堡中有多少个房间?2、最大的房间有多大?

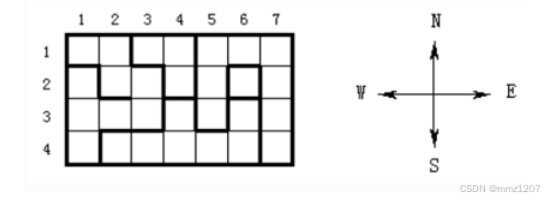
输入格式

平面图用一个数字表示一个方块(第1个房间用二进制1011表示，0表示无东墙，用十进制11表示)。第一行一个整数m(m≤50)，表示房子南北方向的长度。第二行一个整数n(n≤50)，表示房子东西方向的长度。后面的m行，每行有n个整数，每个整数都表示平面图对应位置的方块的特征。每个方块中墙的特征由数字P来描述(0≤P≤15)。数字P是下面的可能取的数字之和:
1(西墙 west)
2(北墙 north)
4(东墙 east)
8(南墙 south)
室内的墙被定义两次:例如方块(1，1)中的南墙也被位于其南面的
方块(2，1)定义了一次。
建筑中至少有两个房间。

输出格式

第1行:1个整数表示房间总数:第2行:1个整数，表示最大房间的面积(方块数)、

样例

输入样例

4
7
11 6 11 6 3 10 6
7 9 6 13 5 15 5
1 10 12 7 13 7 5
13 11 10 8 10 12 13

输出样例

#include <bits/stdc++.h>
using namespace std;
struct node
{
	int x,y,v;
	node(){};
	node(int a,int b,int c)
	{
		x = a;
		y = b;
		v = c;
	}
};
node que[10010];
int a[60][60];
int b[60][60];
int cnt;
int cntt;
int ma;
int n,m;
int head,tail;
int dx[] = {0,1,0,-1};
int dy[] = {1,0,-1,0};


int main()
{
	
	cin>>n>>m;
	for(int i = 1;i<=n;i++)
	{
		for(int j = 1;j<=m;j++)
		{
			cin>>a[i][j];
		}
	}
	cnt = 0;
	ma = 0;
	for(int i = 1;i<=n;i++)
	{
		for(int j = 1;j<=m;j++)
		{
			for(int k = 0;k<=tail;k++)
			{
				que[k] = {0,0,1};
			}
			if(b[i][j]==0)
			{
				cntt = 1;
				head = 0;
				tail = 0;
				que[++tail] = {i,j,0};
				cnt++;
				b[i][j] = cnt;
				while(head<tail)
				{
					head++;
					for(int ii = 0;ii<4;ii++)
					{
						int tx = que[head].x+dx[ii];
						int ty = que[head].y+dy[ii];
						if(ii==0)
						{
							if((a[tx][ty]==2||a[tx][ty]==4||a[tx][ty]==8||a[tx][ty]==6||a[tx][ty]==12||a[tx][ty]==10||a[tx][ty]==14||a[tx][ty]==0)&&b[tx][ty]==0&&tx>=1&&tx<=n&&ty>=1&&ty<=m)
							{
								que[++tail] = {tx,ty,que[head].v+1};
								b[tx][ty] = cnt;
								cntt++;
							}
						}
						else if(ii==1)
						{
							if((a[tx][ty]==1||a[tx][ty]==4||a[tx][ty]==8||a[tx][ty]==5||a[tx][ty]==12||a[tx][ty]==9||a[tx][ty]==13||a[tx][ty]==0)&&b[tx][ty]==0&&tx>=1&&tx<=n&&ty>=1&&ty<=m)
							{
								que[++tail] = {tx,ty,que[head].v+1};
								b[tx][ty] = cnt;
								cntt++;
							}
						}
						else if(ii==2)
						{
							if((a[tx][ty]==2||a[tx][ty]==1||a[tx][ty]==8||a[tx][ty]==3||a[tx][ty]==11||a[tx][ty]==10||a[tx][ty]==9||a[tx][ty]==0)&&b[tx][ty]==0&&tx>=1&&tx<=n&&ty>=1&&ty<=m)
							{
								que[++tail] = {tx,ty,que[head].v+1};
								b[tx][ty] = cnt;
								cntt++;
							}
						}
						else if(ii==3)
						{
							if((a[tx][ty]==2||a[tx][ty]==4||a[tx][ty]==1||a[tx][ty]==6||a[tx][ty]==3||a[tx][ty]==5||a[tx][ty]==7||a[tx][ty]==0)&&b[tx][ty]==0&&tx>=1&&tx<=n&&ty>=1&&ty<=m)
							{
								que[++tail] = {tx,ty,que[head].v+1};
								b[tx][ty] = cnt;
								cntt++;
							}
						}
						
					}
					
				}
				ma = max(ma,cntt);
			}
		}
	}
	
	cout<<cnt<<endl<<ma;
	
	return 0;
}