P3372 【模板】线段树 1

【模板】线段树 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1. 将某区间每一个数加上 $k$。
2. 求出某区间每一个数的和。

输入格式

第一行包含两个整数 $n,m$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 $3$ 或 $4$ 个整数，表示一个操作，具体如下：

1. 1 x y k：将区间 $[x,y]$ 内每个数加上 $k$。
2. 2 x y：输出区间 $[x,y]$ 内每个数的和。

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

样例 #1

样例输入 #1

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

样例输出 #1

11
8
20

提示

对于 $30\%$ 的数据：$n\le 8$，$m\le 10$。
对于 $70\%$ 的数据：$n\le {10}^3$，$m\le {10}^4$。
对于 $100\%$ 的数据：$1\le n,m\le {10}^5$。

保证任意时刻数列中所有元素的绝对值之和 $\le {10}^{18}$。

【样例解释】

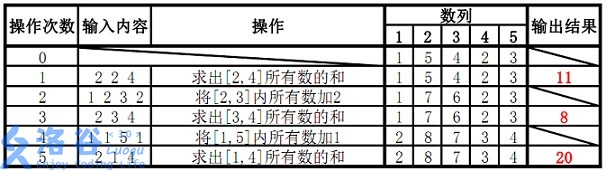
思路

这道题是线段树的简单模板，只要按照格式写就行了。学过的小伙伴们可以直接看代码，我也会有一些注释，不懂得就私聊或评论区发给我吧！

代码

#include<iostream>
using namespace std;
#define ls id<<1//定义左儿子
#define rs id<<1|1//定义右儿子
#define int long long
const int N=1e5+10;
int n,m;
int a[N];
struct node
{
	int l,r,sum,lazy;
}tr[N<<2];//定义结构体类型的线段树数组
void push_up(int id)//向上传递
{
	tr[id].sum=tr[ls].sum+tr[rs].sum;//即当前的总和为左儿子的和与右儿子的和相加
}
void push_down(int id)//向下传递
{
	tr[ls].sum+=tr[id].lazy*(tr[ls].r-tr[ls].l+1);//需要传递的数的总值
	tr[rs].sum+=tr[id].lazy*(tr[rs].r-tr[rs].l+1);//同上
	tr[ls].lazy+=tr[id].lazy;//加上累计值
	tr[rs].lazy+=tr[id].lazy;//同上
	tr[id].lazy=0;//将旧的存储变为零
}
void build(int id,int l,int r)//建树
{
	tr[id].l=l,tr[id].r=r;//初始化数据内容
	tr[id].sum=tr[id].lazy=0;
	if(l==r)//即当前是叶子结点，到底了
	{
		tr[id].sum=a[l];//赋值
		return;
	}
	int mid=l+r>>1;//取平均值
	build(ls,l,mid);//在左边至中间进行建树
	build(rs,mid+1,r);//在中间至右边进行建树
	push_up(id);//向上传递数值
}
void add_tree(int id,int l,int r,int k)//增加数值
{
	if(tr[id].l>r||tr[id].r<l)return;//即不符合当前范围
	if(tr[id].l>=l&&tr[id].r<=r)//即符合当前范围
	{
		tr[id].sum+=(tr[id].r-tr[id].l+1)*k;//累加总共要加的数值
		tr[id].lazy+=k;//lazy加上每个变量需要加的数
		return;
	}
	if(tr[id].lazy)//如果已经有存着的数还没传递
		push_down(id);//向下传递
	add_tree(ls,l,r,k);//左儿子寻找合适范围并增加
	add_tree(rs,l,r,k);//右儿子寻找合适范围并增加
	push_up(id);//向上传递
}
int sum_tree(int id,int l,int r)//求和
{
	if(tr[id].l>r||tr[id].r<l)return 0;//如超过范围则结束
	if(tr[id].l>=l&&tr[id].r<=r)return tr[id].sum;//在范围内则返回sum的值
	if(tr[id].lazy)push_down(id);//如果有值尚未传递，就向下传递
	return sum_tree(ls,l,r)+sum_tree(rs,l,r);//返回左儿子所寻找到的值加上右儿子所寻找到的值
}
signed main()
{
	ios::sync_with_stdio(false);//读写优化
	cin.tie(0);
	cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	build(1,1,n);//建树
	while(m--)
	{
		int opt,l,r,k;
		cin>>opt>>l>>r;
		if(opt&1)
		{
			cin>>k;
			add_tree(1,l,r,k);
		}
		else
			cout<<sum_tree(1,l,r)<<endl;
	}
	return 0;
}

后记

点个赞吧！