试实现邻接表存储图的广度优先遍历。
函数接口定义:
void BFS ( LGraph Graph, Vertex S, void (*Visit)(Vertex) );
其中LGraph是邻接表存储的图,定义如下:
/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
Vertex AdjV; /* 邻接点下标 */
PtrToAdjVNode Next; /* 指向下一个邻接点的指针 */
};
/* 顶点表头结点的定义 */
typedef struct Vnode{
PtrToAdjVNode FirstEdge; /* 边表头指针 */
} AdjList[MaxVertexNum]; /* AdjList是邻接表类型 */
/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数 */
int Ne; /* 边数 */
AdjList G; /* 邻接表 */
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */
函数BFS应从第S个顶点出发对邻接表存储的图Graph进行广度优先搜索,遍历时用裁判定义的函数Visit访问每个顶点。当访问邻接点时,要求按邻接表顺序访问。题目保证S是图中的合法顶点。
裁判测试程序样例:
#include <stdio.h>
typedef enum {false, true} bool;
#define MaxVertexNum 10 /* 最大顶点数设为10 */
typedef int Vertex; /* 用顶点下标表示顶点,为整型 */
/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
Vertex AdjV; /* 邻接点下标 */
PtrToAdjVNode Next; /* 指向下一个邻接点的指针 */
};
/* 顶点表头结点的定义 */
typedef struct Vnode{
PtrToAdjVNode FirstEdge; /* 边表头指针 */
} AdjList[MaxVertexNum]; /* AdjList是邻接表类型 */
/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数 */
int Ne; /* 边数 */
AdjList G; /* 邻接表 */
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */
bool Visited[MaxVertexNum]; /* 顶点的访问标记 */
LGraph CreateGraph(); /* 创建图并且将Visited初始化为false;裁判实现,细节不表 */
void Visit( Vertex V )
{
printf(" %d", V);
}
void BFS ( LGraph Graph, Vertex S, void (*Visit)(Vertex) );
int main()
{
LGraph G;
Vertex S;
G = CreateGraph();
scanf("%d", &S);
printf("BFS from %d:", S);
BFS(G, S, Visit);
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:给定图如下
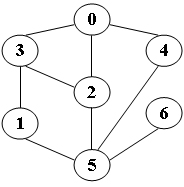
2
输出样例:
BFS from 2: 2 0 3 5 4 1 6
代码长度限制 16 KB
时间限制 400 ms
内存限制 64 MB
一种可能的解答方式:
/** Breadth First Search:广度优先遍历
* 一般而言,用队列来实现,这里可以用数组借助双指针来模拟队列
* LGraph Graph:传入未进行访问过的图,邻接表的方式存储
* Vertex S:起始访问的点
* void (*Visit)(Vertex):传入一个函数的指针,指向一个用于处理顶点的访问操作的函数
**/
void BFS ( LGraph Graph, Vertex S, void (*Visit)(Vertex) ){
// 此节点已经被访问
Visited[S] = true;
// 调用访问函数
Visit(S);
// 因为最大顶点数为10,声明的数组的大小可以粗略估计是100以内
int dispatch[100] = {0};
// 声明数组读取位置和处理位置
int read= 0,write = 0;
// 首节点放入
dispatch[read++] = S;
while(read > write){
// 获取当前读取位置的邻接表头指针
PtrToAdjVNode cur = Graph->G[dispatch[write++]].FirstEdge;
// 如果当前边表的指针存在并且
// 未访问过,则访问和处理然后下一个,
// 访问过则直接看下一个是否符合要求,没有下一个会跳出循环
while(cur){
// 当前邻接点没有访问过就
// 调用访问函数,修改为访问过,读取其邻接的点存入待访问数组
if(!Visited[cur->AdjV]){
Visit(cur->AdjV);
Visited[cur->AdjV] = true;
dispatch[read++] = cur->AdjV;
}
cur = cur->Next;
}
}
}
运行结果:





 文章介绍了如何在邻接表结构的图中实现广度优先搜索(BFS)算法,使用队列模拟,从给定的起始顶点S开始遍历并调用Visit函数处理每个顶点。
文章介绍了如何在邻接表结构的图中实现广度优先搜索(BFS)算法,使用队列模拟,从给定的起始顶点S开始遍历并调用Visit函数处理每个顶点。
















 867
867

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








