PTA 6-5 二叉搜索树中的最近公共祖先

在一棵树T中两个结点u和v的最近公共祖先(LCA)，是树中以u和v为其后代的深度最大的那个结点。现给定某二叉搜索树(BST)中任意两个结点，要求你找出它们的最近公共祖先。

函数接口定义：

int LCA( Tree T, int u, int v );

其中Tree的定义如下：

typedef struct TreeNode *Tree;
struct TreeNode {
    int   Key;
    Tree  Left;
    Tree  Right;
};

函数LCA须返回树T中两个结点u和v的最近公共祖先结点的键值。若u或v不在树中，则应返回ERROR。

裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>

#define ERROR -1
typedef struct TreeNode *Tree;
struct TreeNode {
    int   Key;
    Tree  Left;
    Tree  Right;
};

Tree BuildTree(); /* 细节在此不表 */
int LCA( Tree T,  int u, int v );

int main()
{
    Tree T;
    int u, v, ans;

    T = BuildTree();
    scanf("%d %d", &u, &v);
    ans = LCA(T, u, v);
    if ( ans == ERROR ) printf("Wrong input\n");
    else printf("LCA = %d\n", ans);

    return 0;
}

/* 你的代码将被嵌在这里 */

输入样例1 （对于下图给定的树）：

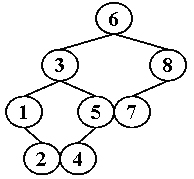
2 7

输出样例1：

LCA = 6

输入样例2 （对于例1中的树）：

1 9

输出样例2：

Wrong input

代码长度限制                                                                                                                        16 KB

时间限制                                                                                                                                400 ms

内存限制                                                                                                                                64 MB

一种可能的解答方法：

// 此函数用于寻找二叉搜索树是否含有值为x的节点
int find(Tree T,int x)
{
    // 如果树为空
    if(!T)
        return 0;
    // 找到了节点返回1，表示找到了
    if(T->Key==x)
        return 1;
    // 当前找的值小于目标值，说明目标x在当前节点的右边，递归遍历右子树
    if(T->Key<x)
        return find(T->Right,x);
    // 当前找的值大于目标值，说明目标x在当前节点的左边，递归遍历左子树
    if(T->Key>x)
        return find(T->Left,x);
}
// 寻找最近的公共祖先
int LCA( Tree T, int u, int v ){
    // 如果树为空，直接返回错误
    if(!T)
        return ERROR;
    // 如果树不存在这俩点，直接返回错误
    if((!find(T,u))||(!find(T,v)))
        return ERROR;
    // 当前的节点等于某个后代，说明已经找到最近的公共祖先
    if((u==T->Key)||(v==T->Key))
        return T->Key;
    // 当前节点刚好在u和v之间，直接返回当前节点（因为是二叉搜索树，
    // 从根节点慢慢往下遍历，第一次遇到的正好卡在中间的节点就是公共祖先，
    // 高一级就会大于或小于所有节点，低一级就不可能是公共祖先了，
    // 也遍历不到那里）
    if((u>T->Key&&v<T->Key)||(u<T->Key&&v>T->Key))
        return T->Key;
    // 目标节点大于当前节点，往右子树递归
    if(u>T->Key)
        return LCA(T->Right,u,v);
    // 目标节点小于当前节点，往左子树递归
    if(u<T->Key)
        return LCA(T->Left,u,v);
}

运行结果：