【Datawhale|天池】心跳信号分类预测 (4) - 模型之 XGBoost

本文链接：https://blog.youkuaiyun.com/ming_hu_yong/article/details/115221800

本文深入探讨了XGBoost算法，从基础的CART决策树到XGBoost的目标函数，包括损失函数、正则化项以及如何通过泰勒展开计算叶子节点权重。此外，还介绍了XGBoost如何通过优化目标函数来构建树结构，如通过一阶和二阶导数来决定分裂点，并分析了其与GBDT的区别。最后，讨论了XGBoost的优化策略，如学习率、特征采样和近似算法，以及如何处理数据稀疏性，以提高训练速度和模型性能。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

本文主要分享自己总结的关于 xgboost 的笔记。

基础知识

基学习器 CART
$L(y_i, \hat y_i) = (y_i - f(x_i))^2 \\ Classification: Gini(D) = \sum_{k=1}^K p_k(1-p_k) = 1 - \sum_{k=1}^K p_k^2$
回归单样本的损失函数，和分类时在数据集D上的基尼指数。f 表示树，f(x) 则是 x 对应的叶子节点的值。

对于分类问题，在 CART 分割时，我们按照 Gini 指数最小来确定分割点的位置。即：
$\; min_{v \in A_V} \; \sum_{i=1}^2 \frac {|D_i|}{|D|} Gini(D_i) \\ bestA, best\_v = arg \; min_{A \in features} [ arg \; min_{v \in A_V} \; \sum_{i=1}^2 \frac {|D_i|}{|D|} Gini(D_i) ]$
XGBoost 的目标函数：

$\sum_{i=1}^nL(y_i, \hat y_i) + \sum_{k=1}^K \Omega (f_k) \\ where \quad L(y_i, \hat y_i) = (y_i - f(x_i))^2 \\ \Omega (f) = \gamma T + \frac12 \lambda ||\omega||^2 = \gamma T + \frac12 \lambda \sum_{j=1}^T ||\omega_j||^2$
假设有 n 个样本，K 棵树。目标函数由两部分构成，第一部分用来衡量预测分数和真实分数的差距，另一部分则是正则化项。正则化项同样包含两部分，T 表示叶子结点的个数，w 表示叶子节点的分数。 $\gamma$ 可以控制叶子结点的个数，λ 可以控制叶子节点的分数不会过大，防止过拟合。

自问自答

常用的参数都有哪些？

一开始，当然是要先设置 booster，一版直接默认用 gbtree 就可以了，另外还有两个常用的全局设置项是 nthread、verbosity。

接下来，几个常用的能影响到模型拟合能力的参数是：

num_boost_round(n_estimators)
max_depth(树的深度)
eta(learning_rate)

然后，有两个正则化、类似于用来控制预剪枝的参数是：

gamma(分裂时目标函数增益的阈值)
min_child_weight(分裂时孩子权重之和的阈值)

另外几个用于控制正则项的参数是：

lambda(这是叶子节点 L2 正则项的系数)
alpha(这是叶子节点 L1 正则项的系数)
subsample(训练数据"被随机采样用来训练"的比例)
colsample_bytree(训练数据的所有特征"被随机选择用来训练一棵树"的比例)

对于数据不平衡问题，可能还用到的重要参数是：

scale_pos_weight(一般设置成正例和负例样本数量的比值)
max_delta_step

如何通过优化目标函数值来计算叶子节点权重？

$\sum_{i=1}^nL(y_i, \hat y_i) + \sum_{k=1}^K \Omega (f_k) \\ where \quad L(y_i, \hat y_i) = (y_i - f(x_i))^2 \\ \Omega (f) = \gamma T + \frac12 \lambda ||\omega||^2 = \gamma T + \frac12 \lambda \sum_{j=1}^T w_j^2$
那么，假设树的结构已经确定，每个叶子节点对应于一部分样本，即可以将决策树表示为一个映射 $R^d \to \{1, 2, ..., T\}$ ，每个 d 维的样本 $x_i$ 可以映射到决策树 T 个叶子节点中的一个，要如何计算对应的叶子节点权重和相应的目标函数值呢？

一种简单粗暴的方法是，对于分类问题，将叶子节点的值设置为该节点样本集中样本数量最多类别；对于回归问题，则设置为标签值的平均。但是，这就完全忽略目标函数的存在了，我们的目标是要最小化目标函数。

以下对目标函数进行一些化简：

假设现在学习到了第 t 棵树，记为 $f_t(x)$ ，那么 $\hat y^t = \hat y^{t-1} + f_t(x)$ 。我们的目标是使得 $\hat y^t$ 尽量等于 $y$ ，即 $ \hat y^{t-1} + f_t(x)$ 尽量趋近于 $y$ ，也就是让 $f_t(x)$ 趋近于 $\hat y^{t-1}$ ，换言之， $\hat y^{t-1}$ 就是当前这棵树的拟合目标，或者说样本的标签值（说起来，这和 GBDT 其实是一样的，只是这里目标函数不同，导致最后拟合出来的叶子节点的权重会有所不同）。代入目标函数中：
$Obj^{(t)} = \sum_{i=1}^n L(y_i, \hat y_i^{t-1} + f_t(x_i)) + \Omega(f_t)$
我们知道有泰勒公式二阶展开：
$\Delta x) = f(x) + f'(x)·\Delta x + \frac 12 f''(x)·(\Delta x)^2$
将 $y_i^{t-1}$ 看作上式中的 x， $f_t(x)$ 看作上式中的 $\Delta x$ ， $L(y_i, \hat y_i^{t-1})$ 看作上式的 $f (x)$ 。那么目标函数可以改写成：
$Obj^{(t)} \approx \sum_{i=1}^{n} [L(y_i, \hat y_i^{t-1}) + g_i f_t(x_i) + \frac 12 h_i f_t^2 (x_i)] + \Omega (f_t)$
这里的 $g_i， h_i$ 分别是 $L(y_i, \hat y_i^{t-1})$ 关于 $\hat y_i^{t-1}$ 的一阶导和二阶导。若以平方误差作为损失函数，即 $L(y_i, \hat y_i^{t-1}) = (y_i - \hat y_i^{t-1})^2$ ，那么有 $g_i = 2(\hat y_i^{t-1} - y_i)$ , $h_i = 2$ 。

由于 $L(y_i, \hat y_i^{t-1})$ 是常数项不影响我们把目标函数最小化，所以上式可以简写成：
$Obj^{(t)} \approx \sum_{i=1}^{n} [g_i f_t(x_i) + \frac 12 h_i f_t^2 (x_i)] + \Omega (f_t)$
假设树的结构已经确定，对目标函数进一步化简：

设每个叶子节点的权重为 $w_j, j \in {1, 2, ..., T}$ ，那么可以将决策树表示成 $w_{q(x)}$ ，即每个样本会映射到第 q(x) 个叶子节点对应的权值。假设 $I_j = \{i|q(x_i) = j\}$ 为第 j 个叶子节点的样本集合，则目标函数可进一步化为：
$Obj^{(t)} \approx \sum_{i=1}^{n} [g_i f_t(x_i) + \frac 12 h_i f_t^2 (x_i)] + \Omega (f_t) \\ = \sum_{i=1}^n [g_i w_{q(x_i)} + \frac 12 h_i w_{q(x_i)}^2] + \gamma T + \frac12 \lambda \sum_{j=1}^T w_j^2 \\ = \sum_{j=1}^T [\sum_{i \in I_j} g_i w_j + \frac 12 \sum_{i \in I_j} h_i w_j^2 + \frac 12 \lambda w_j^2] + \gamma T \\ = \sum_{j=1}^T [(\sum_{i \in I_j} g_i) w_j + \frac 12 (\sum_{i \in I_j} h_i + \lambda) w_j^2] + \gamma T$
我们之前样本的集合，现在都改写成叶子结点的集合，由于一个叶子结点有多个样本存在，因此才有了 $\sum_{i \in I_j} g_i$ 和 $\sum_{i \in I_j} h_i$ 这两项，把这两项简写为 $G_j, H_j$ ，于是上式变成：
$Obj^{(t)} = \sum_{j=1}^T [G_j w_j + \frac 12 (H_j + \lambda) w_j^2] + \gamma T$
假设树的结构已经确定，通过最小化目标函数，求解叶子节点权重：

在当前假设下，上式中只有 $w$ 是变量，这是一个凸函数，为了使其取得最小值，只需要令目标函数一阶导为 0，便可求得：
$\hat w_j = - \frac {G_j}{H_j + \lambda}$
通过求得的叶子节点权重，计算目标函数值：
$Obj^{(t)} = - \frac 12 \sum_{j=1}^T \frac {G_j^2}{H_j + \lambda} + \gamma T$

学习的过程是怎么进行的？

先从总体上进行描述：

学习的过程就是每次拟合一棵树，直到满足停止条件
拟合之前，先计算出每个样本的一阶导（前 t-1 棵树预测值和真实标签值的绝对差值）和二阶导（固定值：2）
用贪心策略生成一棵树
为每个叶子节点计算权值
把新增的决策树加入，这里有个学习率参数，实际上，在这里学习率的作用更多的是控制过拟合。

生成一棵树的具体过程是这样的：

从树的深度为 0 开始，遍历每个特征的每个分割点，寻找到目标函数增益最大的分割点
1. 针对每个特征，把属于该节点的训练样本按特征值升序排列，通过线性扫描的方式来决定该特征的最佳分裂点，并记录下该特征的最大收益(采用最佳分裂点的目标函数增益)
2. 选择收益最大的特征作为分裂特征，该特征的最佳分裂点作为分裂位置
如果收益大于 gamma，且满足 min_child_weight，那么由该节点生长出两个新的节点，每个新节点关联对应的样本集
不断重复以上两个步骤，直到达到树的最大深度or没有满足条件的分割点

这其实是一种贪心策略，因为我们在分割的每一步都尽量使收益最大，即每一步都得到局部最优解，但无法保证一整棵树的收益最大。

本质是梯度提升树，和 GBDT 有什么区别？

我们说 GBDT，一般指的是基于残差(y-f(x)) 的梯度提升树，实际上，如果以误差的平方作为损失函数，那么残差其实就是损失函数关于 f(x) 的负梯度，所以拟合残差就相当于拟合了负梯度（这其实和神经网络中通过梯度下降来训练参数类似），这就是为什么称之为梯度提升树。

xgboost 的在 GBDT 的基础上主要改进了两点，其实从目标函数中都可以看出来。

对于 GBDT，相当于对目标函数中的损失函数这一项进行了一阶泰勒展开，而 XGBoost 用到了二阶展开，更为精确一点；
xgboost 将叶子节点的权重的 L2 范数作为正则项，并直接添加到了目标函数中。

都说 xgboost 效果好，为什么好？

从偏差-方差的角度来理解：

由于决策树本身的灵活性，加上通过 Boosting 的方法，可以通过不断地迭代学习降低偏差；
除了直接在目标函数添加了正则项，还有很多其他措施来减小模型的方差：
1. 比如 subsample，在每一轮只使用一部分随机采样的样本，通过这种随机性来降低前后学习得到的基学习器的依赖(或者说相关性)，其实就是在 Boosting 过程中掺入 Bagging 的思想，用以降低模型的方差。
2. colsample_bytree 也是类似，只不过这里随机采样的不是样本，而是随机选择一部分特征进行训练。

训练速度快，为什么快？

特征间并行：在进行节点的分裂时，需要寻找每个特征的最佳分裂点及其分裂增益，最终选增益最大的那个特征去做分裂，那么不同特征的增益计算就可以并行计算。
决策树的学习最耗时的一个步骤之一就是对特征的值进行排序（因为要确定最佳分割点），xgboost 的做法是在训练之前，预先对数据进行排序，然后保存为block结构，后面的迭代中重复地使用这个结构，大大减小计算量。这个block结构也使得并行成为了可能，在进行节点的分裂时，需要计算每个特征的增益，最终选增益最大的那个特征去做分裂，那么各个特征的增益计算就可以开多线程进行。
近似直方图算法。树节点在进行分裂时，我们需要计算每个特征的每个分割点对应的增益，即用贪心法枚举所有可能的分割点。当数据无法一次载入内存或者在分布式情况下，贪心算法效率就会变得很低，所以xgboost还提出了一种可并行的近似直方图算法，用于高效地生成候选的分割点。
另外，对于训练数据特别稀疏的情况，稀疏感知的分位点寻找算法也能加速训练。

论文阅读笔记

2. 提升树 TREE BOOSTING IN A NUTSHELL

2.1 正则项 Regularized Learning Objective

本节提出了目标函数。其中的正则化项可以防止过拟合。

2.2 泰勒二阶展开 Gradient Tree Boosting

对目标函数二阶泰勒展开。通过最小化目标函数，可以得到叶子节点的权值、以及目标函数值。

分裂前后目标函数值的增益也很容易计算。

2.3 学习率和特征采样（Shrinkage and Column Subsampling）

Shrinkage:

类似于随机梯度下降优化算法中的学习率，Shrinkage 具体做法是对每一轮生成的树的叶子节点权重乘上一个系数 $\eta$ (即希腊字母eta)，这就是为什么 XGBoost 包中学习率参数名称为 eta。

Column Subsampling:

和随机森林里使用的特征采样类似，这是一个 bagging 思想的应用，而且也是第一次被使用在 Tree Boosting 里。效果甚至比传统的 row sub-sampling（样本采样）好。而且，特征采样还能加速训练。

3. 分裂点寻找算法 SPLIT FINDING ALGORITHMS

3.1 精确贪婪算法（Exact Greedy Algorithm）

每一轮boost，生成一棵树。由于枚举所有可能的树结构是NP-hard问题，不可能完成，所以实际做法是，在每次进行节点分裂的时候，以最大化分裂增益（loss reduction）的方式来进行节点的分裂。这是一种贪婪的策略。

事先对训练样本按照特征值排序，可以加速训练。

1562676136590

每一层，对于某一个特征，基于特征列 Block 结构，并行进行所有叶子节点的分裂点寻找。并行的过程，我现在的理解是这样的：

对于某个线程，在顺序遍历某排好序的特征列时，对于每一个特征值，我们都能知道它对应的哪个样本(记为第i个)、哪个叶子节点(记为第 j 个)，也因此就能取得该样本的梯度 $g_i, h_i$ ，并根据 j 计算出 $G_{jL}, H_{jL}$ 和 $G_{jR}, H_{jR}$ 。遍历一趟下来，所有叶子节点在该特征上的最大增益就都出来了。

我之前卡在了这里：就是遍历时，对于每一个特征值，都要计算一遍所有叶子节点的分裂增益，开销应该很大。现在才搞懂，其实只需要计算该特征所在的叶子节点的分裂增益就可以了。这里说的“对于每一个特征值”，指的是每个分裂点前面紧挨着的那个特征值。

你想，对于某个 leaf node ，你只记录了该节点中包含了哪些样本(索引)，你怎么取得这个节点中这些样本的该特征的排序值呢？反正我想了好久就是想不通有啥高效的办法。在这里卡了好久。

所以，其实相当于没有遍历叶子节点这一说，只是，在遍历特征的所有分裂点的过程中，隐式地完成了对所有叶子节点的遍历。这也是为什么 xgb 总是满二叉树。

参考：XGBoost原理及并行实现中的 “method 3” 部分。

3.2 近似算法（Approximate Algorithm）

当数据无法一起加载进内存，或者在分布式环境下，精确贪婪算法效率很低。即便正常情况下，有些连续值特征的取值个数可能非常多，这样计算起来开销很大，而且还容易过拟合。所以可以使用分桶的方式，把特征的取值分割成确定数量的部分。即，我们对每个特征都 propose 对应的候选分裂点们（由加权分位点算法生成，每次生成一系列候选分裂点称作一次proposal），可用于每棵树(global)，或者每次分裂(local)。分桶后，需要汇总每个桶内的 $g_i$ 和 $h_i$ （难道这就是论文中的“construct approximate histograms of gradient statistics”？）。

全局（global）：在树构建之前，确定所有特征的候选分裂点，然后在树的所有层次 split finding 时都使用相同的proposals（即候选分裂点）。这种方法需要较少的proposal steps，但需要更多的候选分裂点（才能达到和local版本相同的效果），因为在每次分裂后，候选点们并没有被提纯。

局部（local）：re-propose after each split. 这样的好处是，每次分裂后，样本减少，纯度更高，相当于对候选分裂点进行了提纯(refine)，所以需要的候选分裂点可以较少。潜在地，也更适合于构建深层的树。

1562676158411

XGBoost支持在单机环境下高效地使用精确贪婪算法，或者在任何环境下使用局部或全局的近似算法。

3.3 加权分位点算法（weighted quantile sketch）

以第 k 个特征为例，对于每一个样本，由前面的 t-1 棵树可以得到其二阶导 h，以此作为该样本的权重。n 个样本的集合记为： $D_k = \{(x_{1k}, h_1), (x_{2k}, h_2), ..., (x_{nk}, h_n)\}$

对样本按照特征值升序排列，那么对于一个值 z，可以得到样本值小于 z 的样本权重之和占所有样本权重之和的比例：
$r_k(z) = \dfrac 1{\sum_{(x,h) \in D_k} h} \cdot \sum_{(x,h)\in D_k, x < z} h$
我们的目标是从该特征的这些取值中找到候选分裂点 ${s_{k1}, s_{k2}, ..., s_{kl}\}$ ，满足：

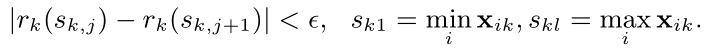
1562681605008

这里 $\epsilon$ 是一个近似系数。直觉上可知，大约有 $\epsilon$ 个候选分裂点。

若使用均方误差作为损失函数，那么实际上所有样本的 h 值都为 2。对于所有样本权重相等的情况，一个已知的分位点算法 quantile sketch 可以解决该问题。

XGBoost支持对样本设置权重，这样一来样本的二阶导 h 也应当乘以相应的权重，这就导致每个样本的权重可以各不相同。本文提出的加权分位点算法可以解决该问题。

3.4 稀疏感知的分裂点寻找（Sparsity-aware Split Finding）

数据稀疏可能由几个原因造成：

数据值缺失
统计值经常为 0
人为的特征工程（比如 one-hot）

当样本的某个数据值缺失时，该样本会被分到默认的分支（获得最大增益的方向）。

具体的算法思路如下：

对于每个特征：
	假设将缺失值分到右分支的情况下，遍历所有特征值不缺失的特征值，寻找最佳分裂点
	再假设将缺失值分到左分支的情况下，遍历所有特征值不缺失的特征值，寻找最佳分裂点
	得到增益最大的分裂点，同时，该最大增益是在哪种假设情况下得到的，哪种假设就作为缺失值的默认分支

需要注意的是，该算法将 non-presence 视作缺失值处理，并按照学得的方向进行分支。

我所理解的 non-presence 是类似于 one-hot 之后的 0 值，不知道对不对？

作者在一个由于 one-hot 导致数据极其稀疏的数据集 Allstate-10K 上进行测试，该稀疏感知算法能比原始算法提升 50 倍的速度。

所以，我的理解是，稀疏感知算法既有效处理了缺失值，又加速了训练。

4. 系统设计 SYSTEM DESIGN

4.1 Column Block for Parallel Learning

训练树的时候，最消耗时间的部分是，对数据进行排序。本文提出一种方法，将数据保存在内存单元里，保存的结构被称为 block。

每一个 block 存储一列特征，在 block 中，特征值已经排好序，并且记录了每个特征值对应的样本索引(这样可以节省大量的存储空间)。block 的数据格式是压缩的列（CSC格式）。Block 中特征之所以记录了指向样本的索引，是为了能根据特征的值来取梯度。

输入数据的排序只在训练开始前计算一次，之后每次迭代都可以复用。

4.2 Cache-aware Access

使用Block结构的一个缺点是取梯度的时候，是通过索引来获取的，而这些梯度的获取顺序是按照特征的大小顺序的。这将导致非连续的内存访问，可能使得CPU cache缓存命中率低，从而影响算法效率。

因此，对于exact greedy算法中, 使用缓存预取（cache-aware prefetching）。具体来说，对每个线程分配一个连续的buffer，读取梯度信息并存入Buffer中（这样就实现了非连续到连续的转化），然后再统计梯度信息。

对于大规模数据，效果十分明显，大约快了一倍。

在 approximate 算法中，对Block的大小进行了合理的设置。定义Block的大小为Block中最多的样本数。设置合适的大小是很重要的，设置过大则容易导致命中率低，过小则容易导致并行化效率不高。经过实验，发现2^16比较好。

4.3 Blocks for Out-of-core Computation

当数据量太大不能全部放入主内存的时候，为了使得out-of-core计算成为可能，将数据划分为多个Block并存放在磁盘上。计算的时候，使用独立的线程预先将Block放入主内存，因此可以在计算的同时读取磁盘。

但是由于磁盘IO速度太慢，通常跟不上计算的速度。因此，需要提升磁盘IO的吞吐量。Xgboost采用了2个策略：

Block压缩（Block Compression）：将Block按列压缩（LZ4压缩算法？），读取的时候用另外的线程解压。对于行索引，只保存第一个索引值，然后只保存该数据与第一个索引值之差(offset)，一共用16个bits来保存
offset，因此，一个block一般有2的16次方个样本。
Block拆分（Block Sharding）：将数据划分到不同磁盘上，为每个磁盘分配一个预取（pre-fetcher）线程，并将数据提取到内存缓冲区中。然后，训练线程交替地从每个缓冲区读取数据。这有助于在多个磁盘可用时增加磁盘读取的吞吐量。