摘要: 分享对论文的理解. 原文见 X. Wang et al., KGAT: Knowledge Graph Attention Network for Recommendation, KDD 2019.
0. 论文贡献
- 在协同知识图谱 (Collaborative knowledge graph) 里显示地对高阶关系建模, 使用项目信息进行更好的推荐系统建模.
- 提出一个新方法 KGAT, 在图神经网络框架下提供高阶模型.
- 又快又好.
- 提供代码: https://github.com/xiangwang1223/knowledge_graph_attention_network.
1. 基础思想
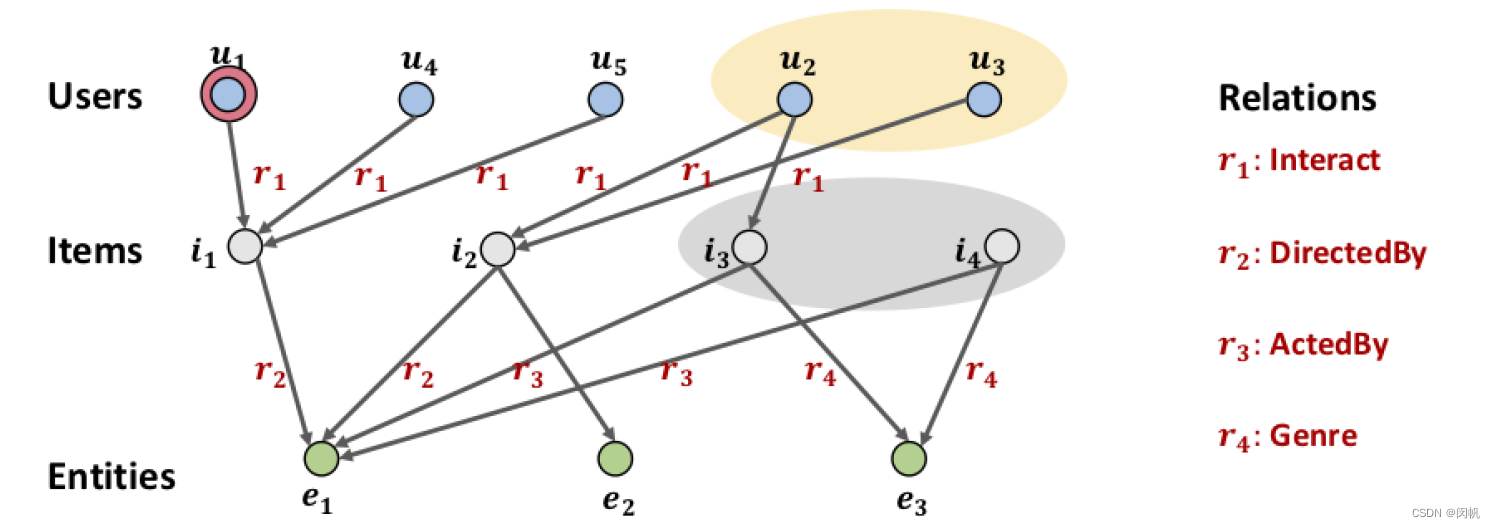
user 与 user, user 与 item 的关系具有一定传递性. 传递的次数即为相应的阶 (order). order = 3 时, u 1 u_1 u1 与 i 3 i_3 i3 和 i 4 i_4 i4 产生联系; order = 4 时, u 1 u_1 u1 与 u 2 , u 3 u_2, u_3 u2,u3 产生联系.
2. 问题建模
| 符号 | 含义 | 备注 |
|---|---|---|
| U \mathcal{U} U | 用户集合 | |
| I \mathcal{I} I | 项目集合 | |
| G 1 \mathcal{G}_1 G1 | 用户-项目二部图 | G 1 ⊆ U × I \mathcal{G}_1 \subseteq \mathcal{U} \times \mathcal{I} G1⊆U×I, 可以认为是有向图 |
| E \mathcal{E} E | 实体集合 | 可以是用户或项目 |
| R \mathcal{R} R | 关系集合 | |
| G 2 \mathcal{G}_2 G2 | 知识图 | G 2 ⊆ E × R × E \mathcal{G}_2 \subseteq \mathcal{E} \times \mathcal{R} \times \mathcal{E} G2⊆E×R×E, 为有向图 |
| A \mathcal{A} A | 项目实体对齐 | A ⊂ I × E \mathcal{A} \subset \mathcal{I} \times \mathcal{E} A⊂I×E |
| G \mathcal{G} G | 统一的知识图 | G ⊆ E ′ × R ′ × E ′ \mathcal{G} \subseteq \mathcal{E}' \times \mathcal{R}' \times \mathcal{E}' G⊆E′×R′×E′ |
| E ′ \mathcal{E}' E′ | 所有实体 | E ′ = E ∪ U \mathcal{E}' = \mathcal{E} \cup \mathcal{U} E′=E∪U, 包含用户、项目、项目的属性 |
| − r -r −r | 关系的逆向 | 电影被演员主演 |
-
用户-项目二部图.
{ ( u , y u i , i ) ∣ u ∈ U , i ∈ I } \{(u, y_{ui}, i) \vert u \in \mathcal{U}, i \in \mathcal{I}\} {(u,yui,i)∣u∈U,i∈I}, y u i = 1 y_{ui} = 1 yui=1 表示用户与项目有联系 (看过电影、买过商品).
吐槽: 搞机器学习的人才写得出来这种模型, 明明就是一个常见的图, 根本不需要 y u i y_{ui} yui. -
项目知识图
{ ( h , r , t ) ∣ h , t ∈ E , r ∈ R ) } \{(h, r, t) \vert h, t \in \mathcal{E}, r \in \mathcal{R})\} {(h,r,t)∣h,t∈E,r∈R)}. -
项目实体对齐
A = { ( i , e ) ∣ i ∈ I , e ∈ E } \mathcal{A} = \{(i, e) \vert i \in \mathcal{I}, e \in \mathcal{E}\} A={(i,e)∣i∈I,e∈E} 有误. 其实 A \mathcal{A} A 是后者的子集. -
问题描述
输入: 协同知识图 G \mathcal{G} G;
输出: y ^ u i \hat{y}_{ui} y^ui, 即用户 u u u 与项目 i i i 有关联 (喜欢, 想要购买) 的可能性.
3. 方法
嵌入 (embedding) 是指为每个实体学习一个向量, 用于表示它.
嵌入之后, 就可以利用向量间的距离计算实体的相似性 (关联性).
4. 疑问
- 明明是一个三部图 (用户、项目、属性), 为什么非得把用户与项目做成二部图,又把项目与属性做成一个知识图谱?





 本文解读了X.Wang等人在KDD2019上提出的KGAT模型,该方法针对协同知识图谱中的高阶关系建模,通过图神经网络实现更精确的推荐。它利用用户-项目二部图和知识图谱结构,有效捕捉实体间复杂联系。疑问部分探讨了为何将用户项目关系和属性分开建模。
本文解读了X.Wang等人在KDD2019上提出的KGAT模型,该方法针对协同知识图谱中的高阶关系建模,通过图神经网络实现更精确的推荐。它利用用户-项目二部图和知识图谱结构,有效捕捉实体间复杂联系。疑问部分探讨了为何将用户项目关系和属性分开建模。

















 4088
4088

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








