深度神经网络优化（二）- Optimization algorithms

第二篇关于优化算法，介绍mini-batch以及momentum, RMSprop和Adam等优化算法

Mini-batch gradient descent

关于mini-batch，机器学习笔记最后一篇有所提及，不再赘述，这里强调三点：

1. mini-batch size 的选择，更倾向于去选择2的次方，一般会考虑16，32，64，128，256，512等数字，这会在某种程度上相对于别的mini-batch size运算更快一点，因为更符合电脑的存储方式。
2. 对于mini-batch，我们一般会进行数据shuffle来打乱数据。
3. 由于样本数不会正好整除我们选择的mini-batch size，所以进行partition来处理最后一组数据。

def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
    
    np.random.seed(seed)            # To make your "random" minibatches the same as ours
    m = X.shape[1]                  # number of training examples
    mini_batches = []
        
    # Step 1: Shuffle (X, Y)
    permutation = list(np.random.permutation(m))
    shuffled_X = X[:, permutation]
    shuffled_Y = Y[:, permutation].reshape((1,m))

    # Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.
    num_complete_minibatches = math.floor(m/mini_batch_size) # number of mini batches of size mini_batch_size in your partitionning
    for k in range(0, num_complete_minibatches):
        mini_batch_X = shuffled_X[:, k * mini_batch_size : (k+1) * mini_batch_size]
        mini_batch_Y = shuffled_Y[:, k * mini_batch_size : (k+1) * mini_batch_size]

        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)
    
    # Handling the end case (last mini-batch < mini_batch_size)
    if m % mini_batch_size != 0:
        mini_batch_X = shuffled_X[:, num_complete_minibatches * mini_batch_size : m]
        mini_batch_Y = shuffled_Y[:, num_complete_minibatches * mini_batch_size : m]

        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)
    
    return mini_batches

Exponentially weighted（moving） averages

在讲解momentum，RMSprop，Adam优化算法之前，引入EMA（指数平均数指标），所谓EWA（EMA），它的公式如下图左上角所示。
在下图中关于days-temperature的图，我们看到蓝色的点代表了真实的数据，那很明显有很多噪点，那如果我们想要了解温度变化的大概趋势呢，我们就需要运用所谓local average（moving average），即对于即将要求取的temperature，我们集合之前5天、10天或者50天的温度求平均值来得到，这样曲线就会平滑。那么所谓的EMA就是一种对于moving average的近似。根据 $\beta$ 的取值，EMA相当于求取的之前 $\frac{1}{1-\beta }$ 天的平均值。
如下图 $\beta =0.9$ ，曲线为红色。 $\beta =0.98$，曲线为绿色。$\beta$ 越大相当于求取平均利用的天数就越多，自然就会越平滑而且越滞后。

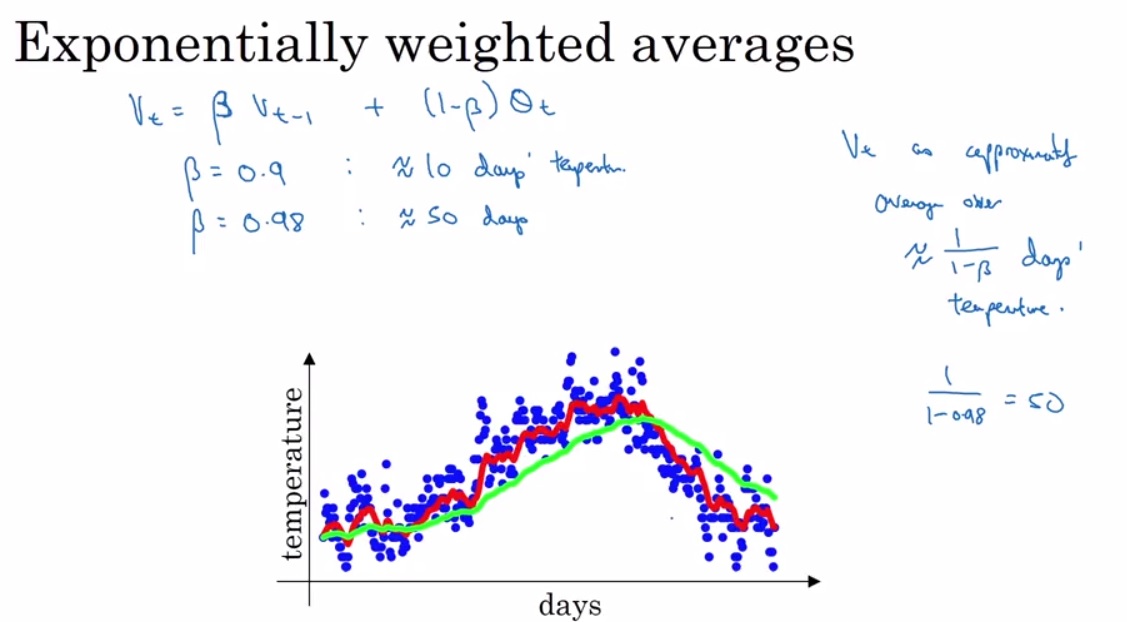
那么为什么我们不直接利用一个移动窗口来计算最近10天或者50天的平均值呢，那是因为，EMA只需要存储两个数据，即当天的温度和前一天算出来的温度，而移动窗口需要记录更多的数据，这将带来更多的运算量。

Bias correction in EMA

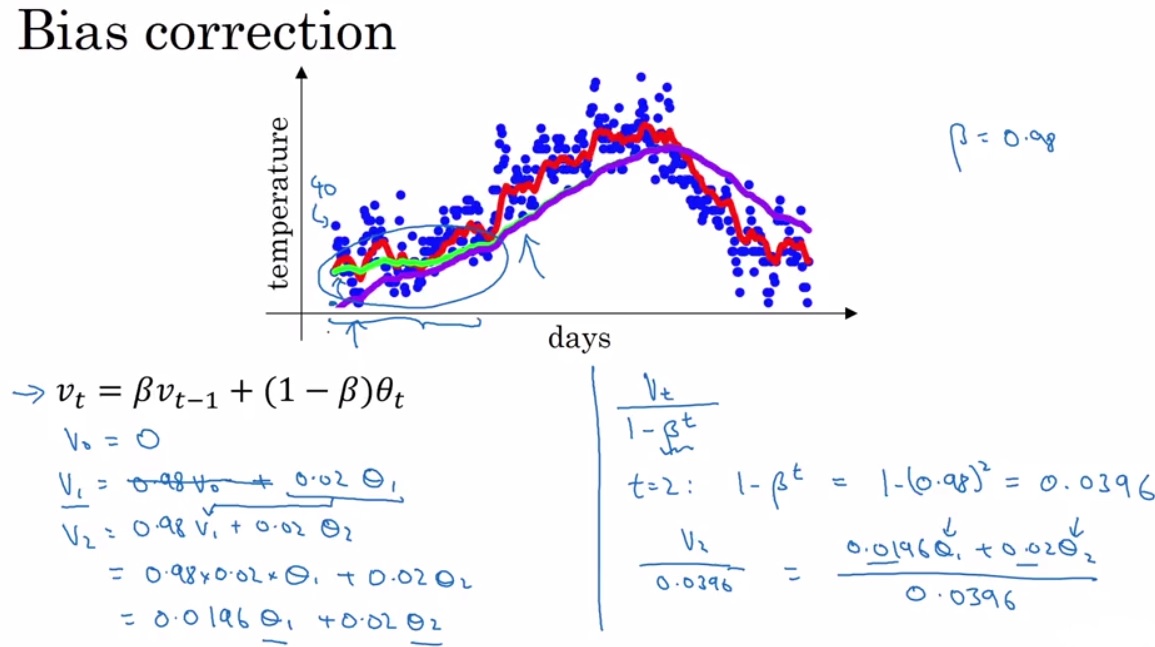
关于EMA的误差矫正，计算 $v_1$ 的时候，我们需要 $v_0$，但是我们没有，于是我们将它初始化为0，那么这将会在我们的前期运算中带来误差，很好理解，我的窗口比如需要囊括之前10天的值，但是现在只有1天的值但是我依然除以了10，这自然就会偏小，如下图紫色曲线，随着时间推移，误差会慢慢消失，所以下图紫色曲线在后面与绿色重合。为了一开始就矫正这种误差呢，我们在每一次迭代之后都进行一次运算操作
$$\frac{v_t}{1-{\beta }^t}$$
这样就不会出现如下情况了。

Gradient descent with momentum

终于来到我们的第一个优化算法，momentum。它的算法如下，你会发现它好像就是用到了我们刚才引入的EMA，对dW,db，分别运用EMA重新计算梯度，然后进行更新。

那么它为什么好呢，下图中，一般的batchGD我们会得到蓝色的曲线，我们发现蓝色曲线在椭圆两侧上下跳动，如果我们采用momentum会是什么结果呢，会变成红色曲线，因为momentum实质上运用的是EMA，EMA实质上是近似moving average，也就是我们会运用最近的几次梯度进行求平均，那么神奇的事情就要出现了，如图纵向的梯度求平均会上下抵消（一正一负），而水平的梯度由于方向一致会保留。那么自然加快了收敛。

RMSprop（root mean square prop）

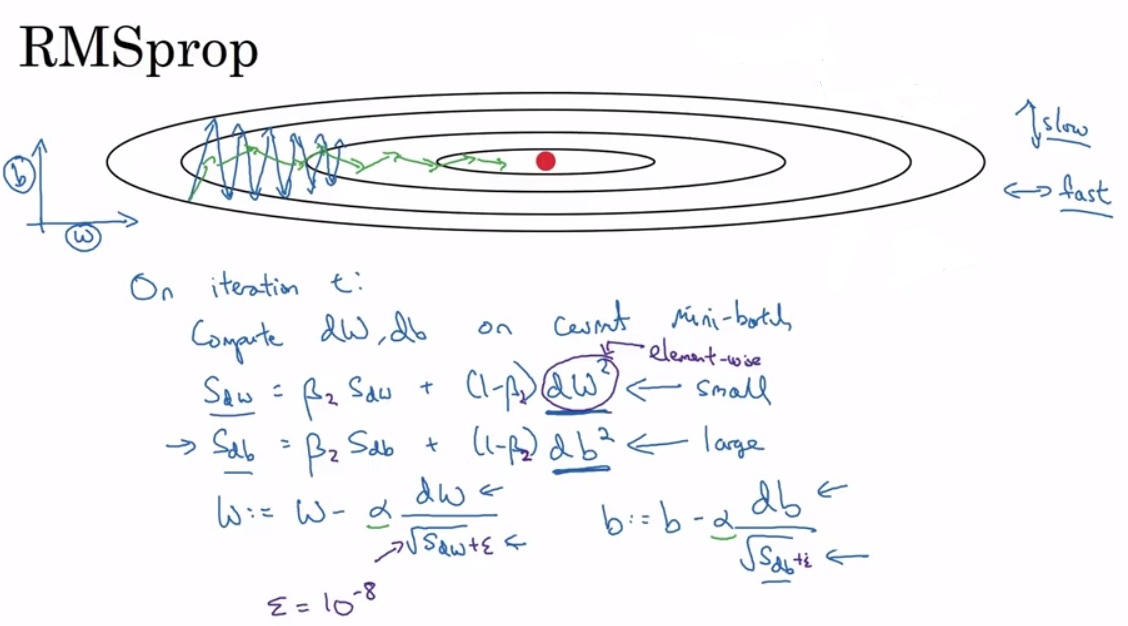
第二个优化算法，RMSprop。同样地也是在EMA的基础上，不过它引入了平方和平方根。如下图，为了方便理解，我们将图中横向和纵向表示为b和W。那么我们希望b的梯度能够缓一点，而W的梯度快一点，由于图中本身b的梯度很大（上下跳跃），那么$d{b}^2$ 就会很大，导致 $s_{db}$ 很大，最终使得 $\frac{db}{\sqrt{s_{db}}}$就小。同理由于dW小，最终$\frac{dW}{\sqrt{s_{dW}}}$就大。那么下图蓝色曲线就会变成绿色。
最后强调一点，一般我们会在梯度下降公式中 $\frac{dW}{\sqrt{s_{dW}}}$ ，$\frac{db}{\sqrt{s_{db}}}$的分母上加上 $ϵ$ 为了防止python对过小的数字进行舍入变成inf。

Adam optimization algorithm

最后一个优化算法，Adam（adaptive momentum estimation）。这是Andrew教授强推的优化算法，因为是实际运用中发现，它适用于大多数的深度学习结构，能够取得很好的效果。Adam本质就是momentum和RMSprop的结合，如下图。

对于超参数$\beta$的取值，$\beta 1$一般取0.9，$\beta 2$一般取0.999.

Learning rate decay

学习速率衰减，有助于优化算法的收敛，不至于在最优解附近跳转。
一般用到的衰减方法有：

1. $$\alpha =\frac{1}{1+\text{decay rate }\ast \text{epoch num}}\ast {\alpha }_0$$
2. $$\alpha =0.95^{\text{epoch num}}\ast {\alpha }_0$$
3. $$\alpha =\frac{k}{\sqrt{\text{epoch num}}}\ast {\alpha }_0$$

The problem of local optimal

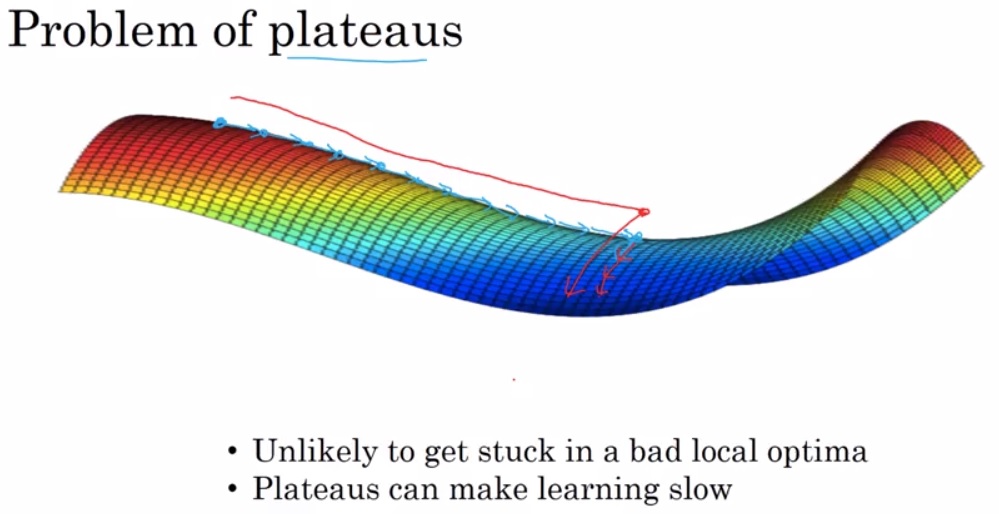
我们知道神经网络的损失函数并不是凸函数，是有很多局部最优解的。但对于深度学习来说，随着参数维度的提高，其实如下图左所示这样的local optimal是很少见的，大多数都是下图右侧的这种鞍点，因为local optimal需要满足所有的参数在该点呈现凸性，这样的概率是很低的。

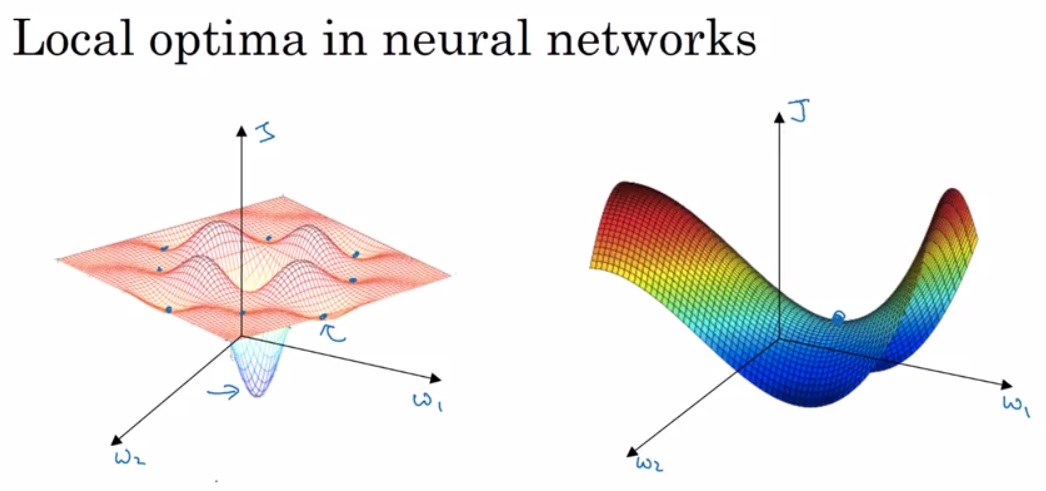
对于这种鞍点呢，最大的问题在于在plateaus上的缓慢下降，会大大增加我们的时间。当然可喜的是，刚才提到的优化算法可以加快我们的收敛，部分解决在plateaus上下降缓慢的问题。

---