COMSOL弱形式解微分方程

COMSOL中建模

在COMSOL中，根据模型向导，选择一维稳态弱形式偏微分方程(w)（数学-＞偏微分方程接口），因变量可以设置为T。

对于几何模型，通过线段间隔 命令建立一段线段，左端点为1，右端点为5。

可以看到COMSOL弱形式偏微分方程(w) 给出的方程形式，我们需要做的就是对被积函数weak 的表达式自定义输入，其默认表达式为-test(Tx)*Tx+1[m^2]*test(T)。

式中Tx表示T对x的导数，test(Tx)则表示Tx的试函数，第一项表示方程（1）中的被积函数，第二项表示热源项，本例不包含热源，因此将其移除。负号是因为 COMSOL 中约定输入框中的表达式在等号（如设定窗口的“方程”栏所示）右侧，而上述推导的方程(1)中的积分则在等号左侧。接下来是处理边界条件，右击弱形式偏微分方程(w)，可以看到COMSOL内置了狄利克雷等多种边界条件，在这里选择自定义边界条件，将鼠标置于更多 项，选择弱贡献。

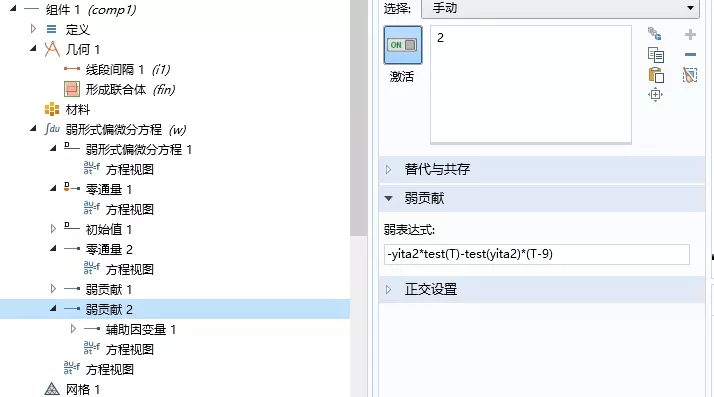
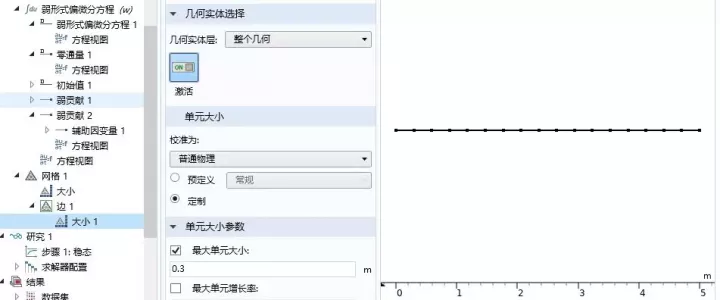
网格划分：右击网格1，选择边，右击边，选择大小(size),单元大小自定义，最大单元大小参数设置为0.3，构建网格。

使用 COMSOL Multiphysics 计算解

现在可以点击计算求解。

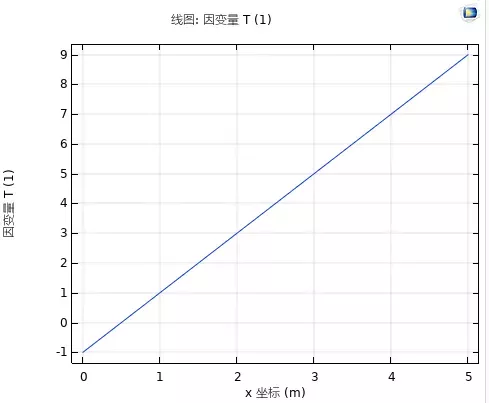
结果是一条斜率为2的直线，左端点处的值为-1，右端点处的值为9。这与T在右端点处值为9，一阶导在左端点处为2，二阶导为0的约束条件一致。