动态规划I
动态规划具备了以下 三个特点:
- 把原来的问题分解成了几个相似的子问题。
- 所有的子问题都只需要解决一次。
- 储存子问题的解。
-
动态规划的本质,是对问题状态的定义和状态转移方程的定义(状态以及状态之间的递推关系)
-
动态规划问题一般从以下四个角度考虑:
- 状态定义
- 状态间的转移方程定义
- 状态的初始化
- 返回结果
适用的场景:最大值/最小值,可不可行,是不是,方案个数
1. Fibonacci数列
1.1 剑指offer10.1—Fibonacci数列
链接:link

解法一:递归的方法也是可以做出来的,但是或许在一定条件限制下就会超时,所以尽量不使用递归的方法,并且它还容易造成栈溢出的情况。
class Solution {
public:
int Fibonacci(int n) {
//可以使用递归的方法来做,但是很有可能会造成超时情况
if(n == 1 || n == 2)
return 1;
return Fibonacci(n-1) + Fibonacci(n-2);
}
};
解法二:你会发现如果使用递归的方法,会存在大量的重复计算,但是如果我们不在倒着求,而是正着求,保留它每一步的结果,那么当我们求F(n)的时候,其实只需要将F(n-1) + F(n-2)相加即可
class Solution {
public:
int Fibonacci(int n) {
vector<int> v(n+1,0);
v[1] = 1;
for(int i = 2;i<=n;++i)
{
v[i] = v[i-1] + v[i-2];
}
return v[n];
}
};
解法三:在不像解法二一样,不保存所有前面的子过程结果,而是使用迭代法的方式
class Solution {
public:
int Fibonacci(int n) {
if(n == 1 || n == 2)
return 1;
int fn1 = 1;
int fn2 = 1;
int ret = 0;
for(int i = 3;i<=n;++i)
{
ret = fn1 + fn2;
fn1 = fn2;
fn2 = ret;
}
return ret;
}
};
类似题型:剑指offer10.2—变态青蛙跳台阶
- 题目:一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法?
- 题解:解法和上面的斐波那契是一样的,既然一次只能够跳一个台阶或者2个台阶,那么f(n) = 最后一步跳一个台阶的总数 + 最后一步跳2个台阶的总数,会发现写出来的代码其实就是上面的结果。
1.2 牛客网—矩形覆盖
链接:link.

题解:
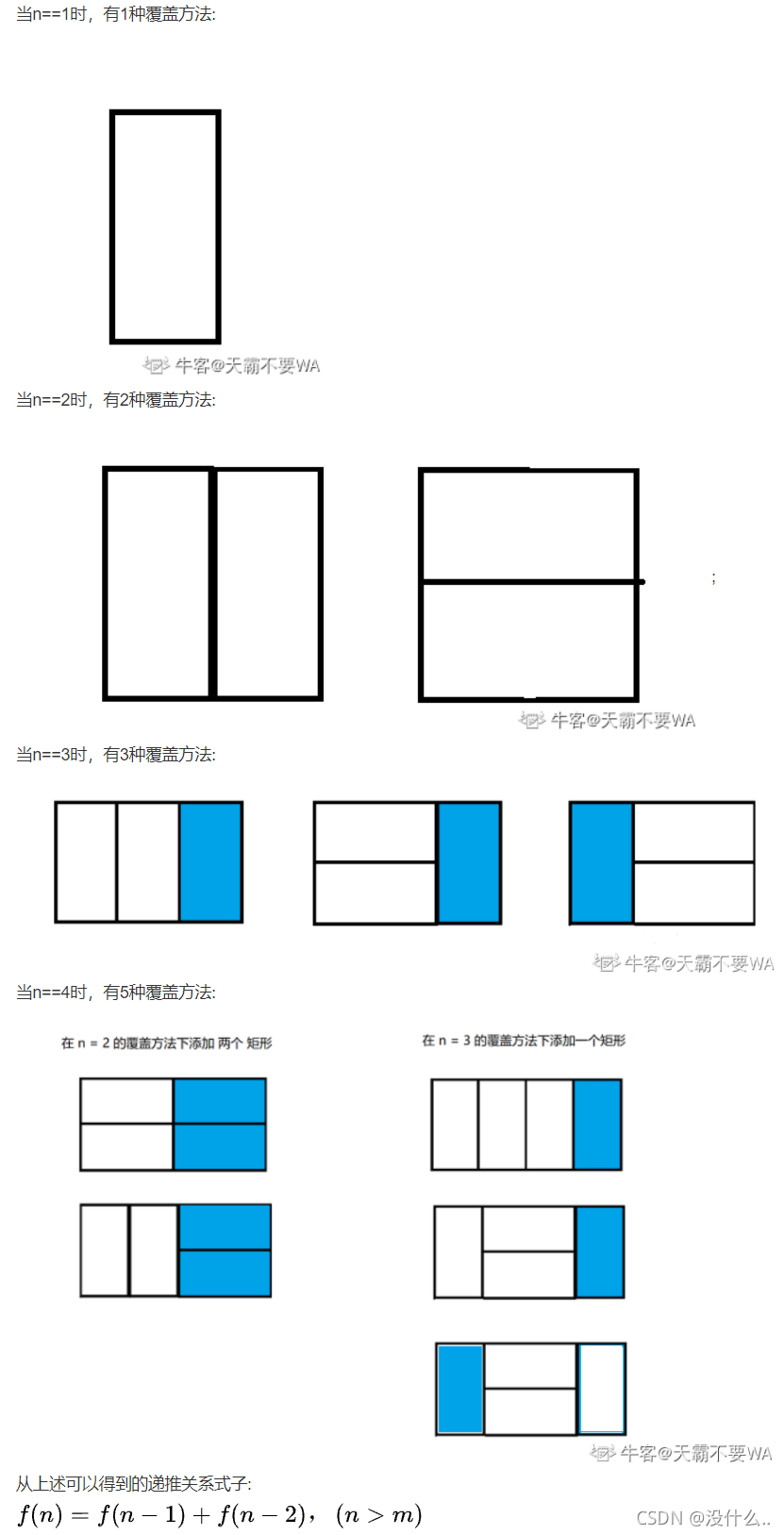
和上面一样也是一种斐波那契类型的题目,要学会灵活应变,方可以变通这类题,本题采用的是迭代的方法。
class Solution {
public:
int rectCover(int number) {
if(number == 0 || number == 1 || number == 2)
return number;
int f1 = 1,f2 = 2,ret = 0;
for(int i = 3;i<=number;++i)
{
ret = f1 + f2;
f1 = f2;
f2 = ret;
}
return ret;
}
};
2. 变态青蛙跳台阶
链接: link.

这道题是对上面那道青蛙跳台阶的的变形,最大的区别就是在于这里不止一次可以跳一个台阶,还能够一次跳n个台阶。
f(n) = f(n-1) + f(n-2) + … + f(0) 最后一个台阶跳一节,那么跳到f(n-1)的方法+最后一个步跳2个台阶,那么要算出跳到f(n-2)的总方法,依次类推下去,发现f(n-1) = f(n-2) + f(n-3)+…+f(0) ,两个一合并,就是f(n) = 2f(n-1) 的递推公式。
class Solution {
public:
int jumpFloorII(int number) {
//F(n) = 2F(n-1);
if(number <= 0)
return 0;
int ret = 1;
for(int i = 1;i<number;++i)
{
ret *= 2;
}
return ret;
}
};
3. 剑指offer42题—最大连续子数组合
链接:https://leetcode-cn.com/problems/lian-xu-zi-shu-zu-de-zui-da-he-lcof/

题解:dp[i]表示以nums[i]为结尾的连续子数组最大和
- dp[i-1] > 0时,dp[i] = array[i] + dp[i-1],说明此时以nums[i-1]为下标的数组和的贡献是正数,那么再加上此时的nums[i]只会将连续子数组和变的更加的大。
- dp[i-1] < 0时,dp[i] = array[i] ,说明此时以nums[i-1]为下标的数组和的贡献是负数。
- 对于前i-1个连续的数组和如果是负数那么对于第i下标的数并不会有贡献,反而成为了累赘,但是如果前i-1个连续的数组和位正,那么对于第i个数是有贡献的。
class Solution {
public:
int maxSubArray(vector<int>& nums) {
if(nums.empty())
return 0;
int sum = nums[0];
int max = nums[0];
for(int i = 1;i<nums.size();++i)
{
sum = std::max(sum+nums[i],nums[i]);
if(sum > max)
{
max = sum;
}
}
return max;
}
};
4. LeetCode第120题—三角形最小路径和
链接:https://leetcode-cn.com/problems/triangle/

题解:
子问题:从(0,0)到达最后一行的(i,j)位置的最小路径和
那么这里需要开始考虑了,谁能够到达(i,j)坐标呢?(i,j) 一> (i+1,j),(i+1,j+1),那么我们在反着推回来,谁能够到达 (i-1,j),(i-1,j-1) 一>(i,j),所开辟的二维数组里面相当于每个位置都存储的是走到当前位置的最小路径和,此时能够求出来所有的,但是还不知道走到最后一行的那个(i,j)下标才是最小的,所以还需要在把最后一行的结果在遍历一遍,比较一下。

class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
//从(0,0)到达最后一行的(i,j)位置的最小路径和
//那么首先得是最后一行那个最小的,如何到达他,作为考虑
if(triangle.empty())
return 0;
int row = triangle.size();
int col = triangle[0].size();
//不再原本的二维数组中进行修改,而是重新和他开辟一个一样的
vector<vector<int>> vv(triangle);
for(int i = 1;i<row;++i)
{
for(int j = 0;j<=i;++j)
{
if(j == 0)
{
vv[i][j] = vv[i-1][j] + triangle[i][j];
}
else if( j == i)
{
vv[i][j] = vv[i-1][j-1] + triangle[i][j];
}
else
{
vv[i][j] = std::min(vv[i-1][j],vv[i-1][j-1]) + triangle[i][j];
}
}
}
//上面是求出来到达每个结点的最小路径和,但是并不知道谁是最小的
//所以还需要从最后一行中选出来最小的
int result = vv[row-1][0];//选最后一行的第一个当最小值
for(int i = 1;i<row;++i)
{
result = std::min(vv[row-1][i],result);
}
return result;
}
};
5. 路径问题
对于这类题,从左上角走到右下角的路径总数,他每次要么往下走要么往右走,只有这两种可能,那么对于右下角这个位置来说,能走到他的也只有他的左边过来,或者上边过来,所以这里就可以把他们切割为子问题,那么走到右下角的路径总数就是,走到左边的位置 + 走到上面的位置路径之和。
5.1 LeetCode第62题—路径总数I
链接:https://leetcode-cn.com/problems/unique-paths/


class Solution {
public:
int uniquePaths(int m, int n) {
//但是也不能无休止的进行下去呀,所以要有一个停止的条件
//你会发现第一行或者第一列能到的路径就只有一条
vector<vector<int>> vv(m,vector<int>(n,1));
for(int i = 1;i<m;++i)
{
for(int j = 1;j<n;++j)
{
vv[i][j] = vv[i-1][j] + vv[i][j-1];
}
}
return vv[m-1][n-1];
}
};
5.2 LeetCode第63题—路径总数II
链接:https://leetcode-cn.com/problems/unique-paths-ii/

题解:这道题和上面的区别就在于或许会遇见障碍物,如果是第一行或者第一列中任意一个位置有障碍物,那么他后面的所有位置都无法到达,是这道题初始化条件需要留意的点。
class Solution {
public:
//1.如果第一行中的任意一个位置有障碍物,那么到达这个位置的路径为0,如果都没有那么到达的就是1
//2.当然列依旧满足
//3.就是要开辟一个m*n的二维数组,用来记录能够到达每一个位置的路径总数,那么最后只需要返回vv[m-1][n-1],因为
//上面已经把能到达(m,n)的全部都已经算出来了,只需要相加就可以了
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
if(obstacleGrid.empty() && obstacleGrid[0].empty())
return 0;
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
vector<vector<int>> vv(m,vector<int>(n,0));
for(int i = 0;i<m;++i)
{
if(obstacleGrid[i][0])
break;
else
vv[i][0] = 1;
}
for(int i = 0;i<n;++i)
{
if(obstacleGrid[0][i])
break;
else
vv[0][i] = 1;
}
for(int i = 1;i<m;++i)
{
for(int j = 1;j<n;++j)
{
if(obstacleGrid[i][j])
{
vv[i][j] = 0;
}
else
{
vv[i][j] = vv[i-1][j] + vv[i][j-1];
}
}
}
return vv[m-1][n-1];
}
};
5.3 剑指offer第99题—最小路径之和
链接:https://leetcode-cn.com/problems/0i0mDW/

题解:对于这类题你会发现其实他们之间是有相通的,我就开辟一个二维数组,专门用来记录走到每个位置所需要的最小路径和,走到右下角的位置只能够是来自于它的左边和上面,所以我只需要从他们两个之间在选择一个较小值即可。对于这个二维数组的第一行和第一列,这里就相当于初始化。

class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
if(grid.empty()|| grid[0].empty())
return 0;
int row = grid.size();
int col = grid[0].size();
//此时的vv里面存的是到达每一个位置的路径总和
vector<vector<int>> vv(row,vector<int>(col,0));
vv[0][0] = grid[0][0];
for(int i = 1;i<row;++i)
{
vv[i][0] = grid[i][0] + vv[i-1][0]; //这个位置有可能会越数组
}
for(int j = 1;j<col;++j)
{
vv[0][j] = grid[0][j] + vv[0][j-1];
}
for(int i = 1;i<row;++i)
{
for(int j = 1;j<col;++j)
{
vv[i][j] = grid[i][j] + std::min(vv[i-1][j],vv[i][j-1]);
}
}
return vv[row-1][col-1];
}
};
5.4 剑指offer47题—礼物的最大价值
LeetCode链接:https://leetcode-cn.com/problems/li-wu-de-zui-da-jie-zhi-lcof/

class Solution {
public:
int maxValue(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
vector<vector<int>> dp(m,vector<int>(n,0));
dp[0][0] = grid[0][0];
//这一步是在初始化第一列
for(int i = 1;i<m;++i)
{
dp[i][0] = dp[i-1][0] + grid[i][0];
}
//这一步是在初始化第一行
for(int j = 1;j<n;++j)
{
dp[0][j] = dp[0][j-1] + grid[0][j];
}
for(int i = 1;i<m;++i)
{
for(int j = 1;j<n;++j)
{
dp[i][j] = std::max(dp[i][j-1],dp[i-1][j]) + grid[i][j];
}
}
return dp[m-1][n-1];
}
};
6. 剑指offer46题—把数字翻译成字符串
LeetCode题目链接:https://leetcode-cn.com/problems/ba-shu-zi-fan-yi-cheng-zi-fu-chuan-lcof/

解题思路:这道题最主要的就是看当前的数字是否能够和前面的数字进行组合,所以的dp数组也是这样进行定义的,前i个数字能够翻译的方法数量。
class Solution {
public:
// dp[i] 表示前i个数的翻译方法数量
int translateNum(int num) {
//对于一个整数你想要确定他的具体某一位其实是不容易的,所以我们把他转换为字符串
string str = to_string(num);
vector<int> dp(str.size() + 1,0);
dp[0] = 1;
dp[1] = 1;
for(int i = 2;i<=str.size();++i)
{
if(str[i-2] == '1' || str[i-2] == '2' && str[i-1] <= '5')
{
//说明此时这一位是可以和前面进行组合的,可以通过123进行推导
//dp[i] = 单独翻译和组合翻译
dp[i] = dp[i-1] + dp[i-2];
}
else
{
//这一位是不影响结果的,因为它必须单独拎出来翻译,就比如126这个数字
dp[i] = dp[i-1];
}
}
return dp[str.size()];
}
};
7. LeetCode第91题—解码方法
LeetCode题目链接:https://leetcode-cn.com/problems/decode-ways/

这道题其实和上面的把数字翻译成字符串有一区同工的地方,但是这里的边界条件以及需要注意的事项更多。其实从题目中也可以读出来一点,那就是对于‘0’是不可以单独翻译的。这才是这道题控制边界的关键
class Solution {
public:
//感觉这道题和把数字翻译为字符串的题型是一样的
//前i个字符解码的总数
//但是这道题还有一个需要注意的点:那就是如果前面那个数字是0,那么这个0不能做前置
//这道题的边界处理我他妈是服了,好像死活解释不同了
//s[i-1] 是否等于'0'这分析边界的关键
int numDecodings(string s) {
int n = s.size();
vector<int> dp(n+1);
if(s[0] == '0')
return 0;
dp[0]= 1;
dp[1] = 1;
for(int i =2;i<=n;++i)
{
//这个就是满足组合的情况,但是此时还需要和前面进行组合
//这个0必须和前面构成组合
if(s[i-2] == '1' || s[i-2] == '2' && s[i-1] <= '6')
{
if(s[i-1] == '0')
dp[i] = dp[i-2];
else
dp[i] = dp[i-2] + dp[i-1];
}
else
{
//这里表示的是前一个字符依旧不满足情况了,此时当前这个还是字符‘0’
//比如说"00" "130"
//这段代码是啥意思,还需要好好想想哦,此时有0压根就不可能出来一个完整的翻译
//因为出现‘0’,即不能够单独翻译,也不能够组合翻译
if(s[i-1] == '0')
return 0;
else
dp[i] = dp[i-1];
}
}
return dp[n];
}
};
8. 剑指offer14题—剪绳子

解题思路:这道题和下面的整数拆分题目是一致的,只不过换了一种表达思路
class Solution {
public:
//这道题脑子就有问题呢,压根就没有思考清楚题目,你仔细看就会发现,这个m并不是题目中所给的,是你自己划分的
int cuttingRope(int n) {
//切割的段数最少都是2
vector<int> dp(n+1,0);
//题目要求剪出来的绳子也是整数长度
for(int i = 2;i<=n;++i)
{
int curMax = 0;
for(int j = 1;j<i;++j)
{
curMax = std::max(curMax,std::max(j*(i-j),j*dp[i-j]));
}
dp[i] = curMax;
}
return dp[n];
}
};
9. LeetCode343题—整数拆分
LeetCode链接:https://leetcode-cn.com/problems/integer-break/

解题思路:
这道题和剪绳子是有相似之处的。

class Solution {
public:
//将其拆分为k个正整数(这个k的大小是>=2的)的和,并使整数的乘积最大化
//dp[i]表示将整数i拆分为k个正整数的乘积的最大值
//其中dp[0] = dp[1] = 0
//当i>=2的时候,第一段截取的长度为j(1<= j<= i-1),那么剩余的就是i-j的长度,要么就不在拆分了,要么继续将i-j拆解为多段,计算
int integerBreak(int n) {
vector<int> dp(n+1,0);
dp[0] = dp[1] = 0;
for(int i = 2;i<=n;++i)
{
int curMax = 0;
//这个j表示的是第一段的长度
for(int j = 1;j<i;++j)
{
curMax= std::max(curMax,max(j*(i-j),j*dp[i-j]));
}
dp[i] = curMax;
}
return dp[n];
}
};
10. LeetCode第96题—不同的二叉搜索树(理解不透彻)
LeetCode链接:https://leetcode-cn.com/problems/unique-binary-search-trees/

解题思路:假设n个节点存在二叉排序树的个数是G(n),1为根节点,2为根节点,…,n为根节点,当1为根节点时,其左子树节点个数为0,右子树节点个数为n-1,同理当2为根节点时,其左子树节点个数为1,右子树节点为n-2,所以可得G(n) = G(0)G(n-1)+G(1)(n-2)+…+G(n-1)*G(0)
class Solution {
public:
//对于题目来说,你首先就应该确定的是什么是二叉搜索树?定义是什么
int numTrees(int n) {
vector<int> dp(n+1);
dp[0] = 1;
for(int i = 1;i<=n;++i)
{
for(int j = 1;j<=i;++j)
{
//:G(n) = G(0)*G(n-1)+G(1)*(n-2)+...+G(n-1)*G(0)
dp[i] += dp[j-1]*dp[i-j];
}
}
return dp[n];
}
};
11. LeetCode第221题—最大正方形

class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
if(m == 0 || n == 0)
return 0;
//dp[i][j] 表示以下标(i,j)为右下角所能构成的最大正方形边长
int Maxside = 0;
vector<vector<int>> dp(m,vector<int>(n,0));
for(int i = 0;i<m;++i)
{
for(int j = 0;j<n;++j)
{
if(matrix[i][j] == '1')
{
if(i == 0 || j == 0)
dp[i][j] = 1;
else
dp[i][j] = std::min(std::min(dp[i][j-1],dp[i-1][j]),dp[i-1][j-1]) + 1;
Maxside = std::max(Maxside,dp[i][j]);
}
}
}
int area = Maxside*Maxside;
return area;
}
};
12. LeetCode第1277题—统计权威1的正方形子矩阵

解题思路:这道题和上面的最大正方形有一区同工的地方,递推方程是一样的,但是他们所代表的意思是不一样的
dp[i][j] 表示的是以下标(i,j)所构成的正方形数量
class Solution {
public:
//这道题其实和最大正方形相同,但是在理解思路上也还是有不同的
//但是递推公式是及其相似的
int countSquares(vector<vector<int>>& matrix) {
//这里的dp[i][j]还表示以该下标(i,j)构成的正方形的个数
int m = matrix.size();
int n = matrix[0].size();
int sum = 0;
vector<vector<int>> dp(m,vector<int>(n));
for(int i = 0;i<m;++i)
{
for(int j = 0;j<n;++j)
{
if(i == 0 || j == 0)
dp[i][j] = matrix[i][j];
else if(matrix[i][j] == 0)
dp[i][j] = 0;
else
dp[i][j] = std::min(std::min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1]) + 1;
sum += dp[i][j];
}
}
return sum;
}
};
参考Blog:























 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








