C++：树和二叉树

C++：树和二叉树

树

定义

• 非线性数据结构
• 能够很好的描述具有分支和层次特性的数据集合

线性数据结构：每一个元素都只与前一个元素和后一个元素相连，如链表等数据结构是线性数据结构。

非线性数据结构：并非每一个元素都只与前一个和后一个元素相连。

基本术语

• 节点（node）：树中的每一个元素
• 子节点/孩子（child node）：一个节点下面，只需一条边相连的节点
• 父节点/父亲（father node）：一个节点上面，只需要一条边相连的节点
• 兄弟节点（sibling node）：父节点相同的子节点
• 根（root)：没有父节点，没有兄弟节点的节点。
• 度（degree）：一个节点拥有的子节点的个数
• 一棵树的度：一棵树中最大的节点度数
• 终端节点/叶子（leaf node）：度为0的节点
• 深度（depth）：树中节点的最深层次数
• 森林（forest）：m（m>=0）棵互不相交的树的集合
• 空树（empty tree）：由0个节点的树组成的和
  
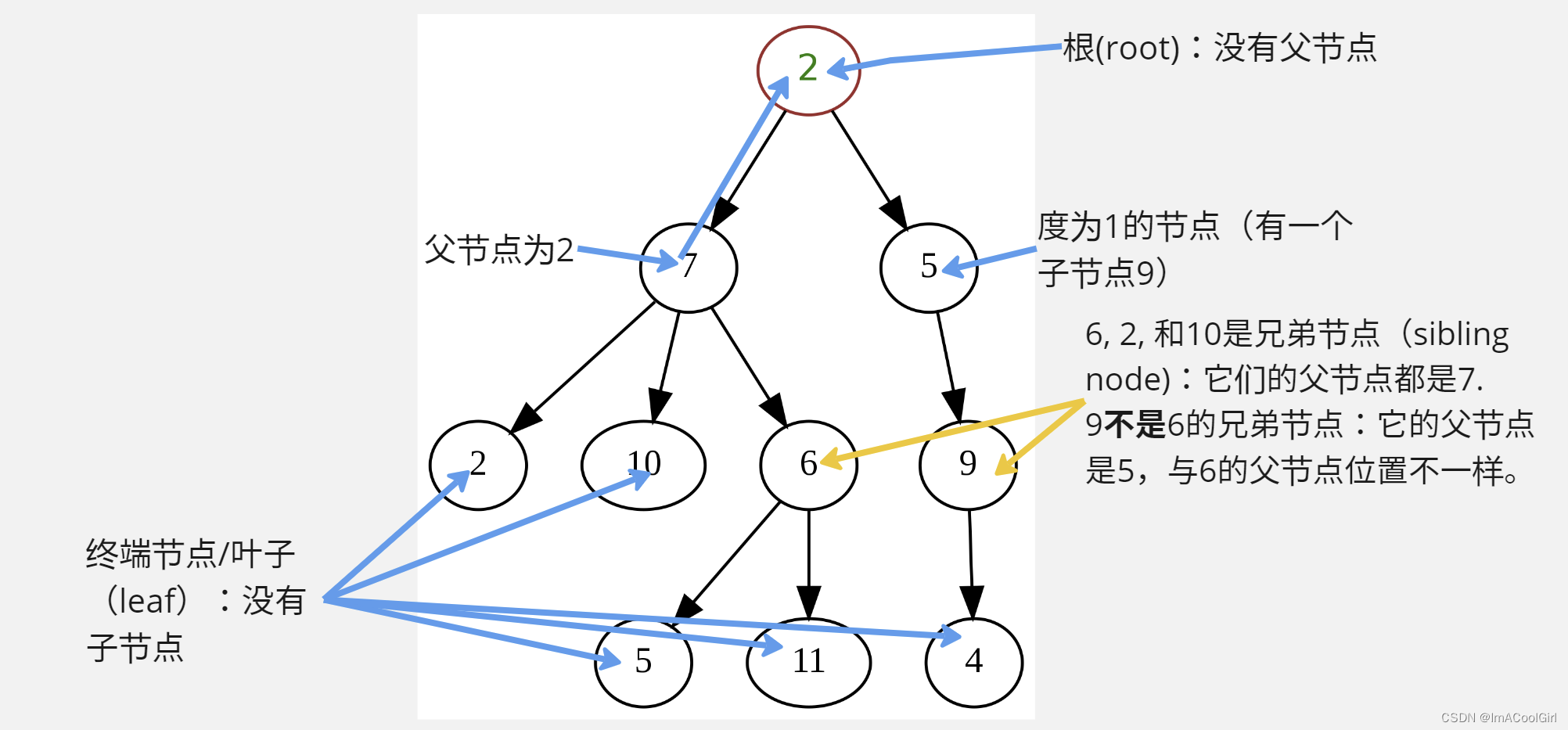
  这棵树的度（degree）是3，因为它所有节点中节点最大的度是3（7的度是3：它的子节点是2，10，和6）。这棵树的深度（depth）是3或者4（有的书和题目规定根的那一层是第0层，其它的规定则认为根的那一层是第1层）。

特征，特点

• 每个元素都是一个节点（node）
• 每棵树，有且仅有一个根（root）
• 树中的每个节点有且只有一个父节点（除根外）
• 子树不相交
• 有N个节点的树有N-1条边

二叉树 (Binary Tree)

定义

一棵树的度为2或以下，它就是一棵二叉树。简单来说，二叉树就是每个节点最多有两个子节点的树。

基本术语

• 左子树：一个节点在左边的子节点
• 右子树：一个节点在右边的子节点

二叉树的五种形式：

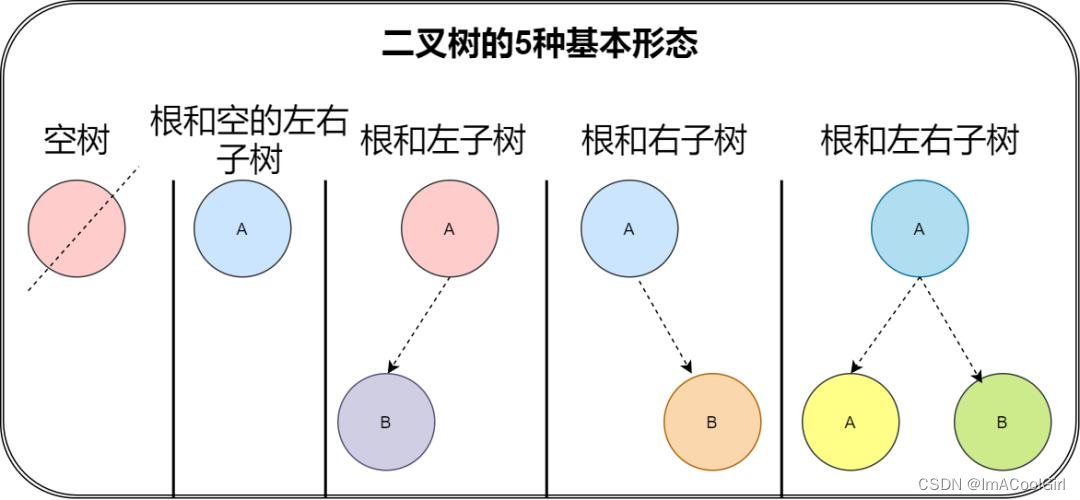
（来源于搜狐网，“二叉树就是这么简单（面试常考点）”）

特殊的二叉树

斜二叉树

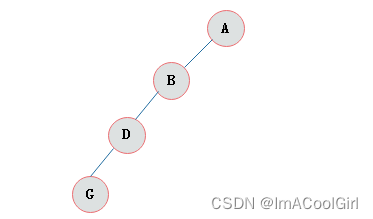
（来源于优快云博客，用户AllenC6的博客“二叉树详解”）
斜二叉树指的是子节点都是左子节点或都是右子节点的二叉树。以上图片是一颗左斜二叉树。

满二叉树/完美二叉树

完美二叉树就是每一个节点（除叶节点外）都有两个子节点的树。如图所示。

完全二叉树

完全二叉树和完美二叉树虽然名字相近，但却不是同一个概念。

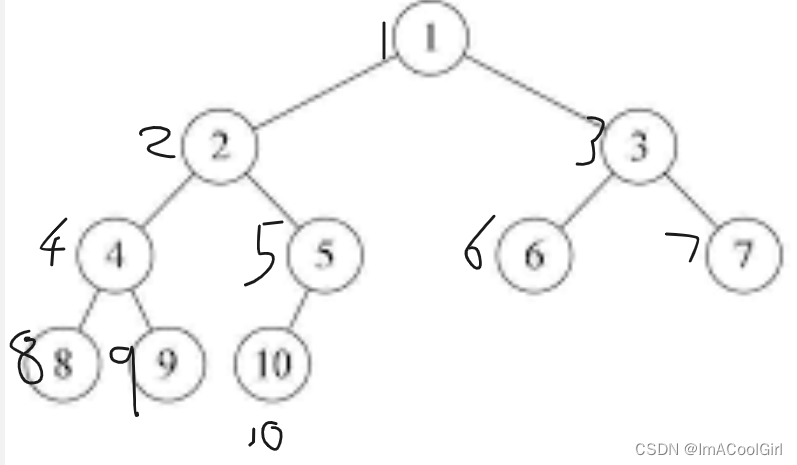
完全二叉树指的是：一棵二叉树，把它的子节点按照从上往下，从左往右的顺着表上序号，并且将与其深度一样的完美二叉树进行同样操作。如果这棵二叉树所有节点的编号与完美二叉树的节点的同样编号位置相同， 这棵树叫做完全二叉树。以上就是一颗完全二叉树。

性质

• 一个二叉树对第i层的最大节点数为:2^i-1，i>=1.
• 深度为k的二叉树最大节点总数为2^k-1，k>=1.
• 对任何非空二叉树，若n0表示叶节点的个数，n2是度为2的非叶节点个数，那么n0=n2+1.

感谢阅读。