LeetCode 62.63. Unique Paths（不同路径）

Unique Paths（不同路径）题目

解析

思路：
拿到这个题目有两种思路，递归和动归。下面分析两种方法的选择理由和可行性。
递归：递归一般用于处理题目中有重复出现的选择和判断的情况，可以套用相同的方法来解决。递归的优点是可以应对各种输入的变化，实现完全的枚举以及剪枝操作。但是当情况复杂的时候，可能会申请过多的空间造成超时或者空间不足，在空间使用很大的情况下也会影响到时间的。在这题可以用递归来求解，但是当m和n数值比较大的情况下时间是不够用的，于是我们不选择它。
动归：动态规划的选择一般基于题目中有求解目标并且可以抽象出轴维度的题。这题有坐标，求解目标是路径数。那么可以很容易发现状态就是每个格子到目标的路径，状态转移方程就是相邻格子之间的路径关系。在这题使用动态规划的优点是只要O（n^2）的时间复杂度就可以完成任务，后面的格子的状态都是基于前面格子的状态。
状态：
int[][] dp=new int[m][n];
初值：
dp[0][0]=1;
状态转移方程：
边界都是1，其他位置的状态都是右侧和下方的状态之和。

if(i!=0||j!=0){
       	if(i==0){
       			dp[i][j]=dp[i][j-1];
       		}else if(j==0){
       			dp[i][j]=dp[i-1][j];
       		}else{
       			dp[i][j]=dp[i][j-1]+dp[i-1][j];
       		}
 }

边界处理:

if(m<0||n<0){
   return 0;
}

完整代码：

class Solution {
    public int uniquePaths(int m, int n) {
    	if(m<0||n<0){
    		return 0;
    	}
        int[][] dp=new int[m][n];
        dp[0][0]=1;
        for(int i=0;i<m;i++){
        	for(int j=0;j<n;j++){
        		if(i!=0||j!=0){
	        		if(i==0){
	        			dp[i][j]=dp[i][j-1];
	        		}else if(j==0){
	        			dp[i][j]=dp[i-1][j];
	        		}else{
	        			dp[i][j]=dp[i][j-1]+dp[i-1][j];
	        		}
        		}
        	}
        }
        return dp[m-1][n-1];    	
    }  
}

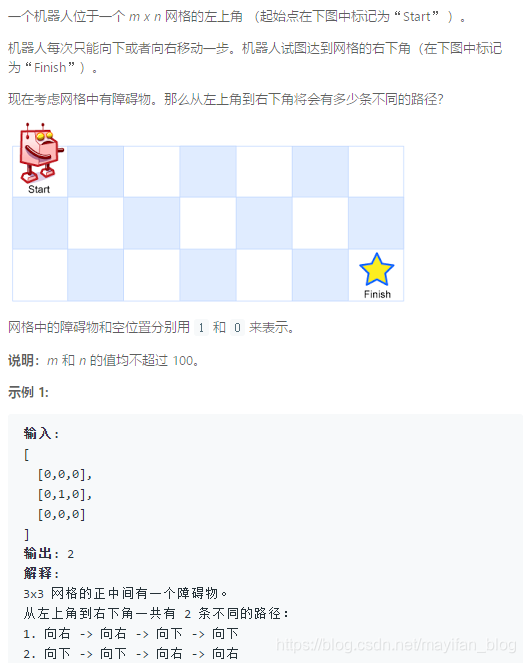
Unique Paths II（不同路径II）题目

解析

思路：
这题加上了障碍物。依然使用动态规划求解，在遇到障碍物的时候把dp值赋0就可以了。
代码：

public class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
    	int m=obstacleGrid.length;
    	int n=obstacleGrid[0].length;
    	if(m<0||n<0){
    		return 0;
    	}
        int[][] dp=new int[m][n];
        dp[0][0]=1;
        for(int i=0;i<m;i++){
        	for(int j=0;j<n;j++){
        		if(obstacleGrid[i][j]==1){
        			dp[i][j]=0;
        		}else{
	        		if(i!=0||j!=0){
		        		if(i==0){
		        			dp[i][j]=dp[i][j-1];
		        		}else if(j==0){
		        			dp[i][j]=dp[i-1][j];
		        		}else{
		        			dp[i][j]=dp[i][j-1]+dp[i-1][j];
		        		}
	        		}
        		}
        	}
        }
        return dp[m-1][n-1];    
    }
}