广度优先遍历之求两点之间的最短距离

# -*- coding: UTF-8 -*-
'''
   *****************LLL*********************
   * @Project ：leetcode                       
   * @File    ：lll_106求顶点到各个节点的最短路径.py
   * @IDE     ：PyCharm             
   * @Author  ：LLL                         
   * @Date    ：2022/5/31 9:45             
   *****************************************
'''
from collections import deque

# 邻接表来表示图
graph = {
    1: {2, 3},
    2: {1, 4},
    3: {1, 4},
    4: {2, 3, 5},
    5: {4}
}


# 广度优先遍历求解最短距离
def bfs_min_distance(root, target):
    queue = deque()
    visited_dic = {node: False for node in graph}  # 记录节点是否被访问
    d_dic = {node: 0 for node in graph}  # 记录根节点到每一个节点的最短路径
    path_path = {node: None for node in graph}  # 记录每一个节点的直接前驱

    # 首先将根节点加入队列中
    queue.append(root)
    while len(queue):
        cur_node = queue.popleft()

        neighbor_nodes = graph[cur_node]
        for neighbor_node in neighbor_nodes:
            if not visited_dic[neighbor_node]:  # 如果相邻的节点没有被访问就加入到队列中
                queue.append(neighbor_node)
                path_path[neighbor_node] = cur_node  # 前驱为当前节点
                d_dic[neighbor_node] = d_dic[cur_node] + 1  # 到根节点的距离=前驱节点到根节点的距离+1

        visited_dic[cur_node] = True  # 当前节点已被访问

    # 根节点到目标节点的路径
    end = target
    path = [end]
    while end:
        end = path_path[end]
        path.append(end)
    path.pop()
    path.reverse()

    return path, d_dic[target]


if __name__ == '__main__':
    print(bfs_min_distance(1, 4))

其实原理上还是广度优先遍历(或者说是层序遍历可能会更形象一些)，只不过除了需要一个队列来记录访问的顺序外，这里额外定义了3个字典保存一些附带的信息：

        visited_dic = {node: False for node in graph}  # 记录节点是否被访问

        d_dic = {node: 0 for node in graph}  # 记录根节点到每一个节点的最短路径
        path_path = {node: None for node in graph}  # 记录每一个节点的直接前驱

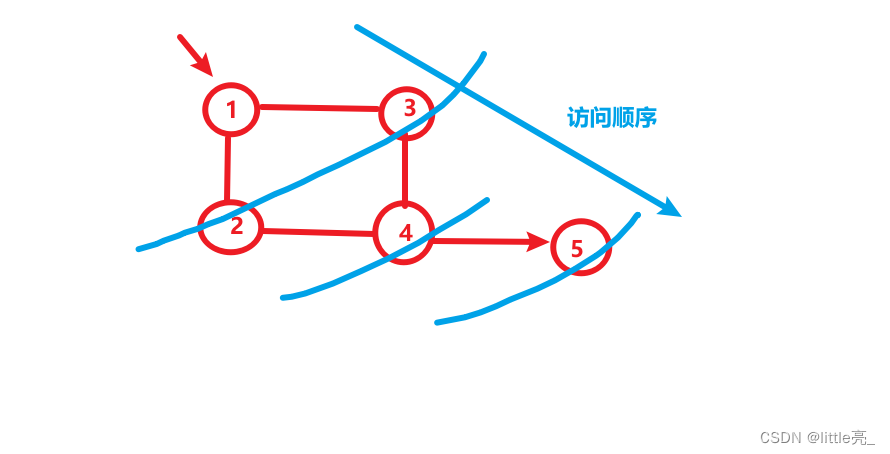
 访问到当前节点时，首先获取当前节点的邻接节点，然后遍历这些邻接节点，只要是没有访问的邻接节点就将其加入队列中，然后更新这个邻接节点的前驱（就是当前节点），然后更新根节点到这个邻接节点的距离（到根节点的距离=前驱节点到根节点的距离+1），最后修改当前节点为已访问的。（这个可能有点不好理解，所以要想搞懂最好可以拿一张草稿画一下这个过程）

访问每一个节点的操作都是如上重复的操作，直到访问到所有节点为止。

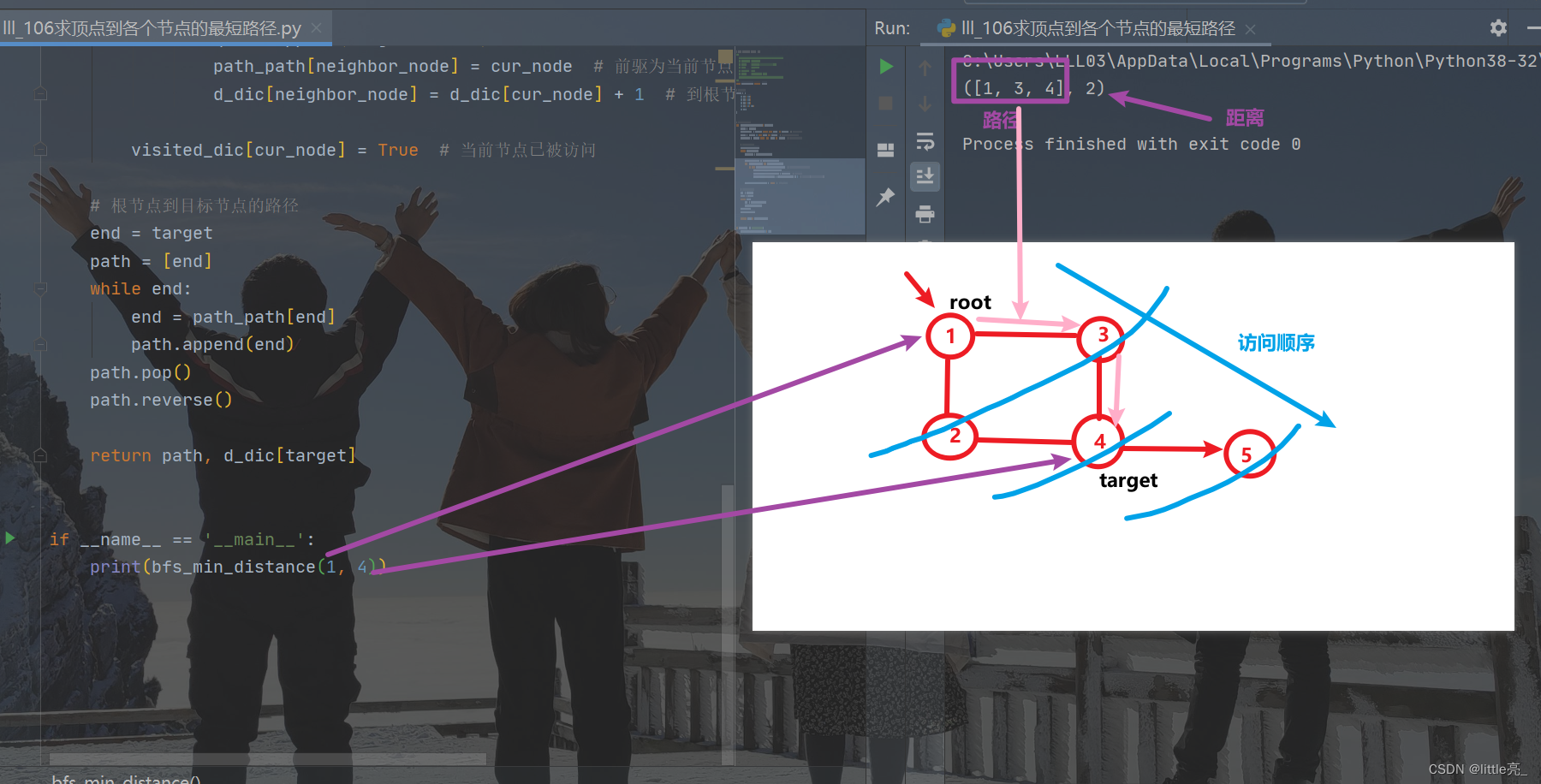
同步更新于个人博客系统： 广度优先遍历之求两点之间的最短距离