✅作者简介:热爱数据处理、建模、算法创新的Matlab仿真开发者。
🍎更多Matlab代码及仿真咨询内容点击 🔗:Matlab科研工作室
🍊个人信条:格物致知。
🔥 内容介绍
多智能体系统控制近年来发展迅速,其在机器人集群、无人机编队、交通流控制等领域展现出巨大的应用潜力。其中,蜂拥控制作为一种重要的多智能体协同控制策略,致力于实现智能体间的自组织和集体行为,例如聚集、分离、一致性等。本文将深入探讨两种典型的蜂拥控制策略:单个领导者-跟随者模式和四个领导者多智能体蜂拥控制,并结合Matlab仿真进行分析与比较。
一、 单个领导者-跟随者模式
单个领导者-跟随者模式是一种相对简单的蜂拥控制策略。系统中存在一个领导者智能体,其余智能体均为跟随者。跟随者智能体根据自身状态以及对领导者状态信息的感知,调整自身运动轨迹以跟随领导者。这种模式的优势在于实现简单、计算量较小,易于理解和实现。然而,其缺点也十分明显:领导者智能体失效将导致整个系统瘫痪,系统的鲁棒性较差;领导者需要具备全局信息或较强的感知能力,这在实际应用中可能难以满足。
在该模式下,跟随者智能体的控制算法通常基于距离和角度信息。例如,可以采用基于人工势场的算法,通过设计斥力项和引力项来模拟跟随者与领导者以及其他跟随者之间的相互作用。斥力项避免跟随者之间发生碰撞,引力项引导跟随者向领导者靠近。具体的算法可以表达为:
distance = sqrt((x(i) - leader_x)^2 + (y(i) - leader_y)^2);
angle = atan2(leader_y - y(i), leader_x - x(i));
% 计算控制力
fx = Kp * (leader_x - x(i)) + Kd * (0 - vx(i)); %比例+微分控制
fy = Kp * (leader_y - y(i)) + Kd * (0 - vy(i));
% 更新速度和位置
vx(i) = vx(i) + fx * dt;
vy(i) = vy(i) + fy * dt;
x(i) = x(i) + vx(i) * dt;
y(i) = y(i) + vy(i) * dt; 其中,Kp和Kd分别为比例增益和微分增益,dt为时间步长。上述代码仅为简化示例,实际应用中需要考虑更多因素,例如障碍物规避、通讯延迟等。
二、 四个领导者多智能体蜂拥控制
为了提高系统的鲁棒性和适应性,可以采用多个领导者来引导跟随者。本节研究采用四个领导者引导跟随者进行蜂拥控制的策略。四个领导者可以形成一个虚拟的“中心”,跟随者围绕该中心进行运动。这种策略可以有效避免单个领导者失效带来的问题,并提升系统的整体性能。
四个领导者的位置可以预先设定,也可以动态调整。动态调整策略可以根据环境变化或任务需求调整领导者的位置,使系统能够更好地适应复杂环境。跟随者智能体可以根据与四个领导者的距离和角度信息,计算一个加权平均的控制力,以引导自身运动。权重可以根据距离进行设计,距离越近,权重越大。
具体的算法可以表达为:)
weight = 1./(distance.^2 + eps); % 添加 eps 防止除零错误
weight = weight ./ sum(weight); % 归一化权重
% 计算加权平均控制力
fx = sum(weight .* (leader_x - repmat(x(i),4,1)));
fy = sum(weight .* (leader_y - repmat(y(i),4,1)));
% 更新速度和位置 (与单个领导者模式类似)
% ...
该代码同样是一个简化示例,实际应用中需要根据具体情况调整权重计算方法和控制算法。
三、 Matlab仿真与结果分析
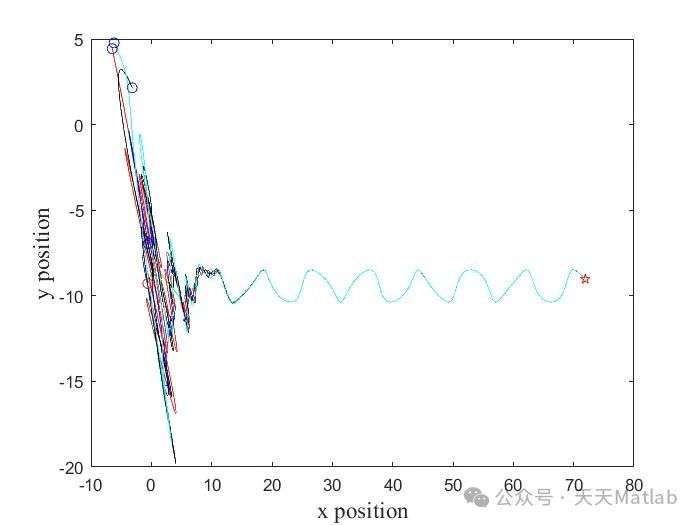
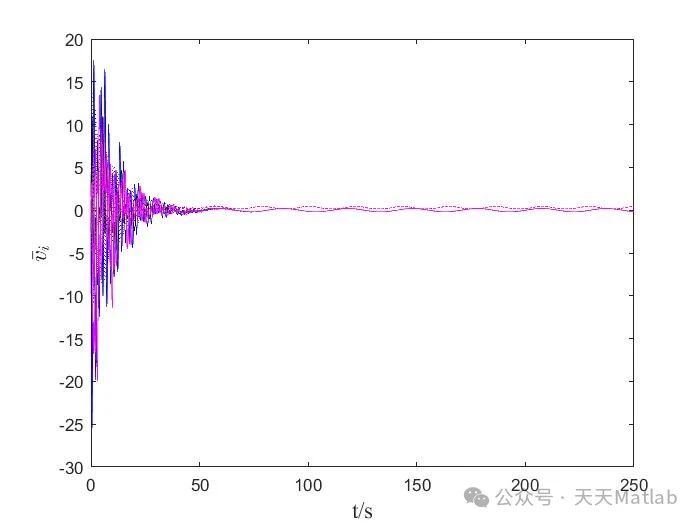
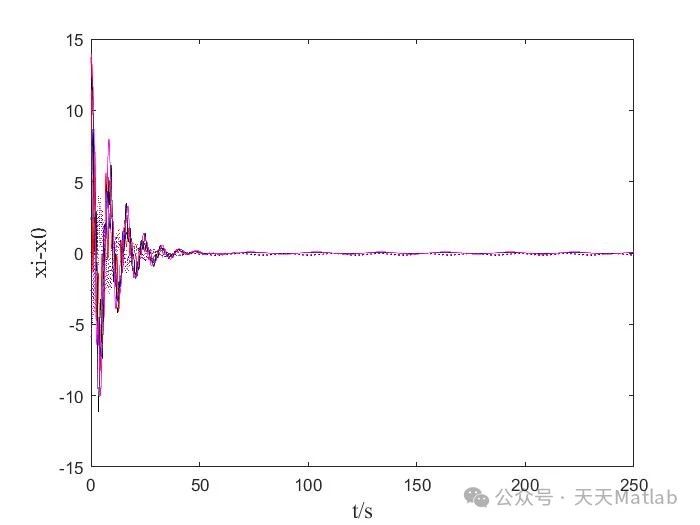
基于上述算法,我们可以利用Matlab进行仿真实验,验证不同策略的有效性和性能。通过改变领导者数量、跟随者数量、控制参数等,可以观察系统在不同情况下的行为。仿真结果可以直观地展现不同策略的优势和不足,为实际应用提供参考。 (此处应包含具体的Matlab仿真代码和结果图表,由于篇幅限制,这里省略。)
四、 结论与未来研究方向
本文研究了单个领导者-跟随者模式和四个领导者多智能体蜂拥控制两种策略,并通过Matlab仿真进行了验证。结果表明,四个领导者模式在鲁棒性和适应性方面优于单个领导者模式。未来研究可以关注以下几个方面:
-
更复杂的控制算法: 研究更先进的控制算法,例如基于模型预测控制、强化学习等,以提高系统的性能和鲁棒性。
-
环境适应性: 研究如何在复杂环境中,例如存在障碍物、动态目标等情况下,实现有效的蜂拥控制。
-
通讯拓扑结构: 研究不同通讯拓扑结构对系统性能的影响,并优化通讯策略以降低通讯负担。
-
容错机制: 设计有效的容错机制,以提高系统对智能体失效的容忍度。
总而言之,多智能体蜂拥控制是一个充满挑战和机遇的研究领域。通过不断改进控制算法和策略,多智能体蜂拥控制技术将在未来的智能化系统中发挥越来越重要的作用。 进一步的研究将致力于提高算法的效率和鲁棒性,并探索其在更多实际应用场景中的可能性。
⛳️ 运行结果
🔗 参考文献
🎈 部分理论引用网络文献,若有侵权联系博主删除
🌈 各类智能优化算法改进及应用
生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化、背包问题、 风电场布局、时隙分配优化、 最佳分布式发电单元分配、多阶段管道维修、 工厂-中心-需求点三级选址问题、 应急生活物质配送中心选址、 基站选址、 道路灯柱布置、 枢纽节点部署、 输电线路台风监测装置、 集装箱调度、 机组优化、 投资优化组合、云服务器组合优化、 天线线性阵列分布优化、CVRP问题、VRPPD问题、多中心VRP问题、多层网络的VRP问题、多中心多车型的VRP问题、 动态VRP问题、双层车辆路径规划(2E-VRP)、充电车辆路径规划(EVRP)、油电混合车辆路径规划、混合流水车间问题、 订单拆分调度问题、 公交车的调度排班优化问题、航班摆渡车辆调度问题、选址路径规划问题、港口调度、港口岸桥调度、停机位分配、机场航班调度、泄漏源定位
🌈 机器学习和深度学习时序、回归、分类、聚类和降维
2.1 bp时序、回归预测和分类
2.2 ENS声神经网络时序、回归预测和分类
2.3 SVM/CNN-SVM/LSSVM/RVM支持向量机系列时序、回归预测和分类
2.4 CNN|TCN|GCN卷积神经网络系列时序、回归预测和分类
2.5 ELM/KELM/RELM/DELM极限学习机系列时序、回归预测和分类
2.6 GRU/Bi-GRU/CNN-GRU/CNN-BiGRU门控神经网络时序、回归预测和分类
2.7 ELMAN递归神经网络时序、回归\预测和分类
2.8 LSTM/BiLSTM/CNN-LSTM/CNN-BiLSTM/长短记忆神经网络系列时序、回归预测和分类
2.9 RBF径向基神经网络时序、回归预测和分类






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










