【信号处理】基于STFT的阶次分析附matlab代码

 ✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，

代码获取、论文复现及科研仿真合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab完整代码及仿真定制内容点击👇

智能优化算法       神经网络预测       雷达通信      无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机

🔥 内容介绍

基于短时傅里叶变换（STFT）的阶次分析是信号处理领域的一个重要研究方向。STFT是一种将信号分解为时间和频率的方法，它可以帮助我们理解信号在不同时间和频率上的特性。阶次分析则是对信号进行分解并提取其阶次信息的过程，通过阶次分析可以得到信号的频率成分和其对应的振幅信息，从而可以更好地理解信号的特性和行为。

STFT的阶次分析在许多领域都有着广泛的应用，比如音频处理、图像处理、通信系统等。在音频处理中，我们可以利用STFT的阶次分析来提取音频信号的频率成分，从而实现音频的分析和合成。在图像处理中，STFT的阶次分析可以帮助我们理解图像在不同频率上的特性，从而实现图像的压缩和增强。在通信系统中，STFT的阶次分析可以帮助我们理解信号在不同频率上的传输特性，从而实现信号的调制和解调。

STFT的阶次分析在实际应用中有着诸多挑战和难点。首先，STFT的阶次分析需要对信号进行时频分解，这就需要选择合适的窗函数和频率分辨率，以及合适的时间和频率分辨率。其次，STFT的阶次分析需要对信号进行谱分解，这就需要选择合适的谱分解方法和参数，以及合适的阶次提取方法和参数。最后，STFT的阶次分析需要对信号进行阶次提取和重构，这就需要选择合适的阶次提取方法和参数，以及合适的重构方法和参数。

为了克服这些挑战和难点，我们可以采用一些有效的方法和技术。首先，我们可以采用自适应窗函数和频率分辨率，以及自适应时间和频率分辨率，来实现STFT的阶次分析。其次，我们可以采用自适应谱分解方法和参数，以及自适应阶次提取方法和参数，来实现STFT的阶次分析。最后，我们可以采用自适应阶次提取方法和参数，以及自适应重构方法和参数，来实现STFT的阶次分析。

总之，基于STFT的阶次分析是一个重要的信号处理方法，它在许多领域都有着广泛的应用。尽管在实际应用中存在着诸多挑战和难点，但我们可以通过采用一些有效的方法和技术来克服这些挑战和难点，从而实现STFT的阶次分析。希望未来能有更多的研究和实践工作，来进一步完善和发展基于STFT的阶次分析方法，为信号处理领域的发展做出更大的贡献。

📣 部分代码

function [mltc]=mltcurve(TFR,freq,tm,fs,m)​mltc=zeros(m,length(tm));​for i=1:m    %extract the ith curve    [tfs,~]=ecurve(TFR,freq,fs);    mltc(i,:)=tfs(1,:);​    %block the ith curve in TFR    for ss=1:length(tm)        hl=round(tfs(2,ss)/(freq(2)-freq(1))+1);        hh=round(tfs(3,ss)/(freq(2)-freq(1))+1);        TFR(hl:hh,ss)=zeros((hh-hl+1),1);​    end​end​end​​​​​​​​

⛳️ 运行结果

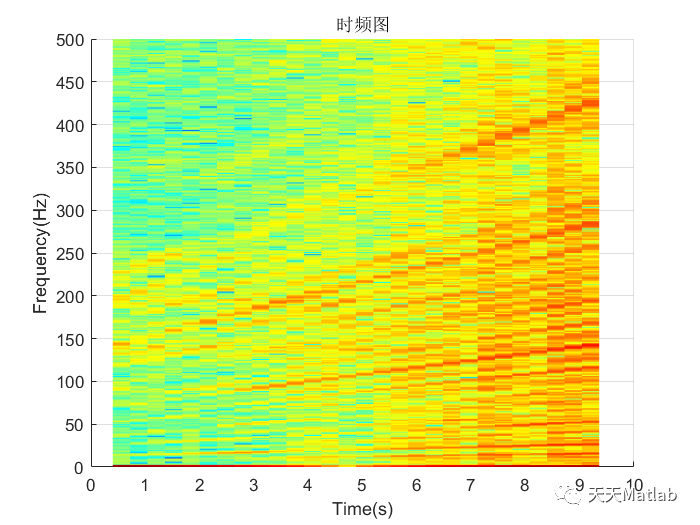
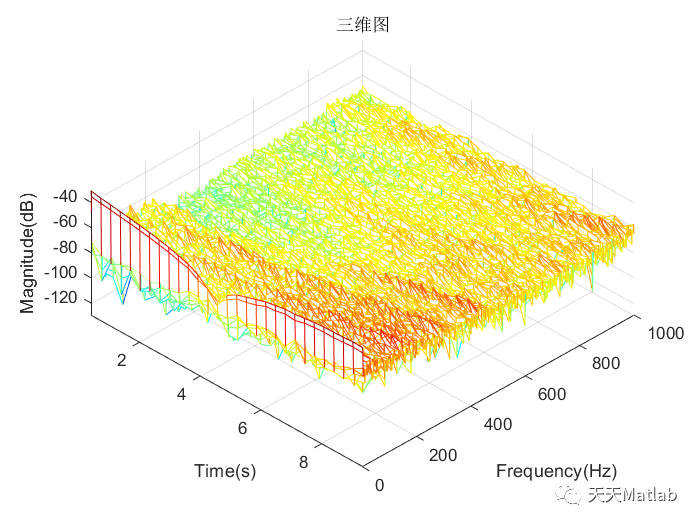
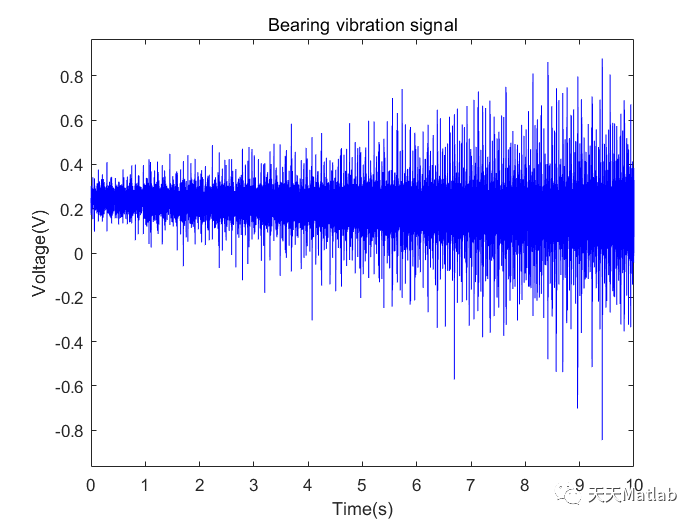
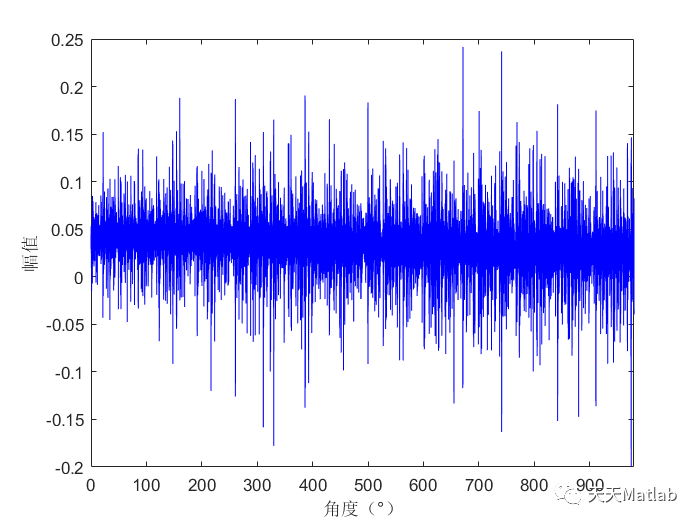
🔗 参考文献

[1] 谢斌.基于MATLAB的时频分析在心电信号分析中的研究与应用[D].陕西师范大学,2012.DOI:CNKI:CDMD:2.1012.424667.

[2] 陆建涛,马会杰,李舜酩,等.一种基于阶次分析和稀疏编码的旋转机械微弱故障信号提取方法.CN202010644002.X[2023-12-11].

[3] 吴康,金阳,周秦.基于STFT和FPO的旋转机械阶次分析[J].湖北汽车工业学院学报, 2023.

🎈 部分理论引用网络文献，若有侵权联系博主删除

🎁  关注我领取海量matlab电子书和数学建模资料

👇  私信完整代码、论文复现、期刊合作、论文辅导及科研仿真定制

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面

卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合