数据插值与拟合

  在工程测量和科学实验中，所得到的数据通常是离散的，要得到这些离散点以外的其他点的数值，就需要根据已知的数据进行插值。插值函数一般由线性函数、多项式、样条函数或这些函数的分段函数充当。

一维插值

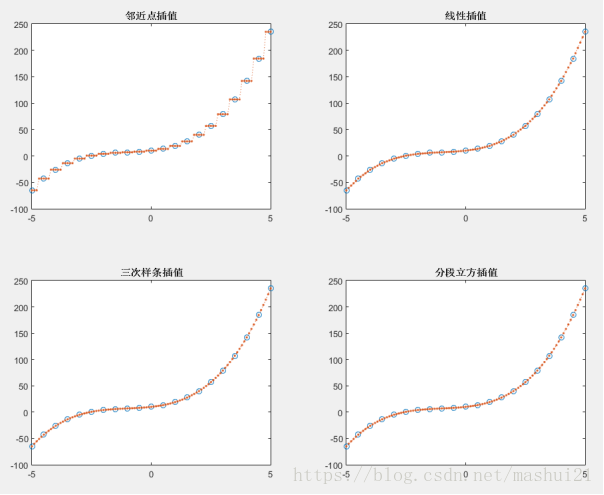
  一维差值:被插值函数只有单一变量，常见的插值函数有临近点插值(nearest)，线性插值(linear)，三次样条插值(spline)和分段立方插值(cubic/pchip)。

  调用形式：

  yi=interp1(x,y,xi,method);

  其中：x为自变量的取值向量，y为x对应的因变量，method为插值方法。

x=[-5:0.5:5];
y=(x.^3)*34+3*x;
x1=[-5:0.1:5]; y1=interp1(x,y,x1,'nearesr');

<