【回归算法解析系列13】神经网络回归（Neural Network Regression）

---

【回归算法解析系列】神经网络回归（Neural Network Regression）

---

1. 神经网络回归：深度学习的回归之道

神经网络回归（Neural Network Regression）通过多层非线性变换捕捉复杂数据关系，核心优势包括：

1. 万能近似定理：可拟合任意连续函数。
2. 自动特征工程：隐层自动学习高阶特征组合。
3. 多模态输入：支持图像、文本、时序等混合数据输入。

适用场景：

• 高维非线性数据（如医学影像预测生物年龄）。
• 多源异构数据融合预测（如用户行为+图像+文本的购买力预测）。
• 实时动态系统建模（如自动驾驶车辆控制）。

---

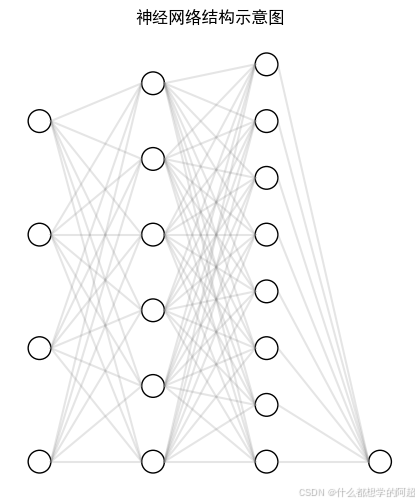
2. 数学原理：从感知机到深度网络

2.1 前向传播公式

对于含 ( L ) 层的全连接网络，第 ( l ) 层输出：
[
\mathbf{z}^{(l)} = \mathbf{W}^{(l)} \mathbf{a}^{(l-1)} + \mathbf{b}^{(l)}, \quad \mathbf{a}^{(l)} = g^{{(l)}(\mathbf{z}}{(l)})
]
其中 ( g^{(l)} ) 为激活函数（如ReLU, Sigmoid）。

2.2 损失函数与反向传播

常用MSE损失：
[
J(\mathbf{W}, \mathbf{b}) = \frac{1}{2N} \sum_{i=1}^N (y_i - \hat{y}_i)^2
]
通过链式法则计算梯度：
[
\frac{\partial J}{\partial \mathbf{W}^{(l)}} = \delta^{(l)} \mathbf{a}^{(l-1)T}, \quad \delta^{(l)} = (\mathbf{W}^{(l+1)T} \delta^{(l+1)}) \odot g’^{{(l)}(\mathbf{z}}{(l)})
]

2.3 激活函数对比

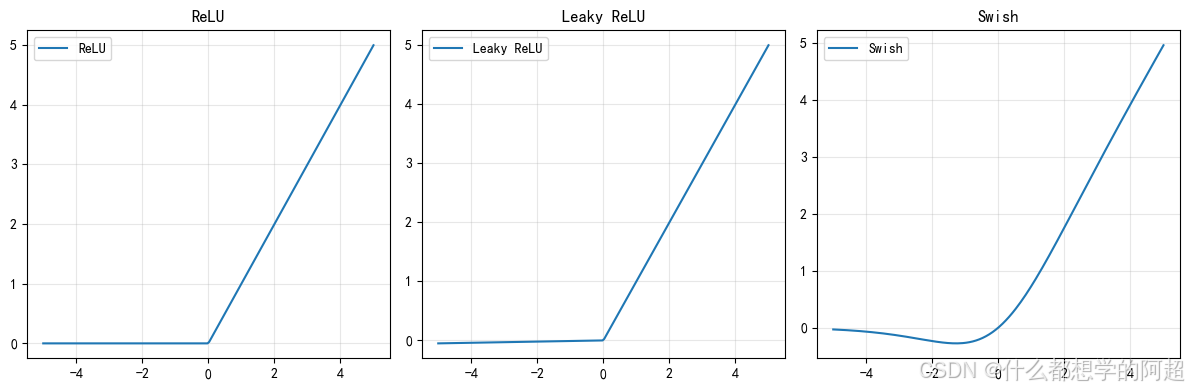
函数	公式	特性
ReLU	( \max(0, x) )	缓解梯度消失，计算高效
LeakyReLU	( \max(0.01x, x) )	解决神经元"死亡"问题
Swish	( x \cdot \sigma(\beta x) )	平滑输出，自门控机制

---

3. 代码实战：图像年龄预测

3.1 数据集准备（UTKFace）

import tensorflow as tf
from tensorflow.keras.preprocessing.image import ImageDataGenerator

# 数据增强配置
train_datagen = ImageDataGenerator(
    rescale=1./255,
    rotation_range=20,
    width_shift_range=0.2,
    horizontal_flip=True
)

# 加载UTKFace数据集
train_generator = train_datagen.flow_from_directory(
    'UTKFace/train',
    target_size=(128, 128),
    batch_size=32,
    class_mode='raw'  # 直接读取年龄数值
)

3.2 构建卷积神经网络

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Dense, Flatten

model = Sequential([
    Conv2D(32, (3,3), activation='relu', input_shape=(128,