什么是堆?
堆是特殊的完全二叉树
什么是完全二叉树?
两种情况:
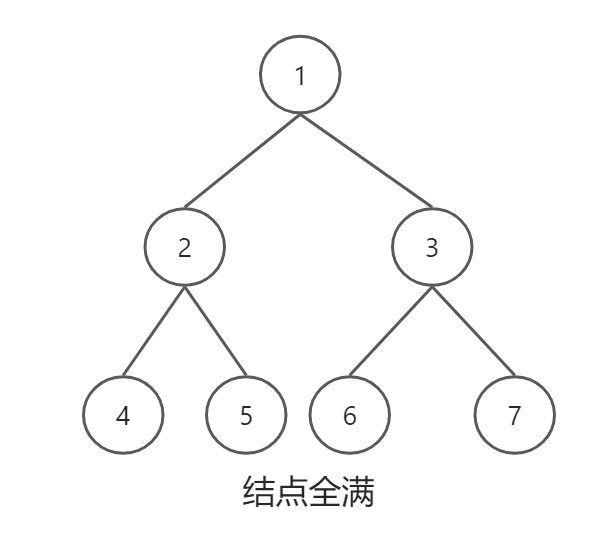
- 二叉树结点全满,为满二叉树
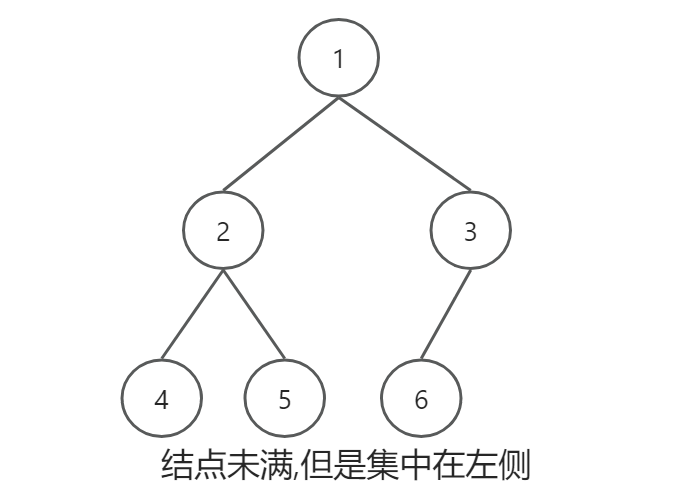
- 二叉树结点除了最后一层全满,并且最后一层有的结点全集中在左侧
堆分两种:大根堆,小根堆
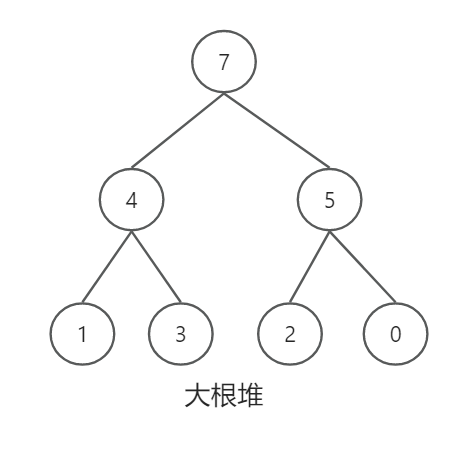
大根堆: 每个节点的值都大于左右孩子点的值
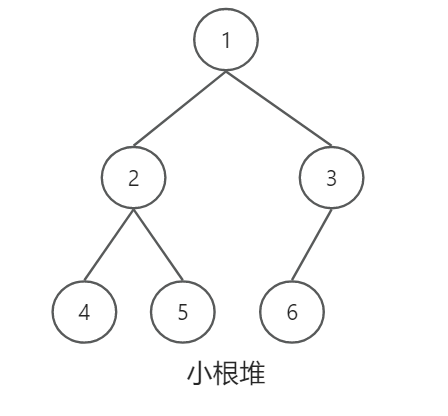
小根堆: 每个节点的值都小于左右孩子点的值
如何表示堆
一般用数组来表示,数组内元素顺序是二叉树的层次遍历
例如:上方的小根堆可以用[1,2,3,4,5,6]来表示
上方的大根堆可以用[7,4,5,1,3,2,0]来表示
因此可以得出:
- 父节点索引i --> 孩子节点索引 i*2以及i*2+1
- 反之可得孩子节点索引i --> 父节点索引 (i-1) / 2
堆的使用---堆排序
注意!!!!企业中的面试常常出现堆排序!!!!!
堆排序思想:
- 首先将乱序的数组构成大根堆,此时能够发现由于大根堆的特性,会导致目前数组最大值在堆的顶端
- 将根节点的元素与最后一个元素交换,即最大的元素已经放在最后,需要排序的数组变成[0,len-1]
- 由于最后一个元素放入根元素,重新构成大根堆
- 重复2,3动作,直到排序完成
注意:一般升序用大根堆,降序使用小根堆
如何构造大根堆?
分析: 大根堆是由父节点,孩子节点构成为单元组成的数据结构
思路如下:
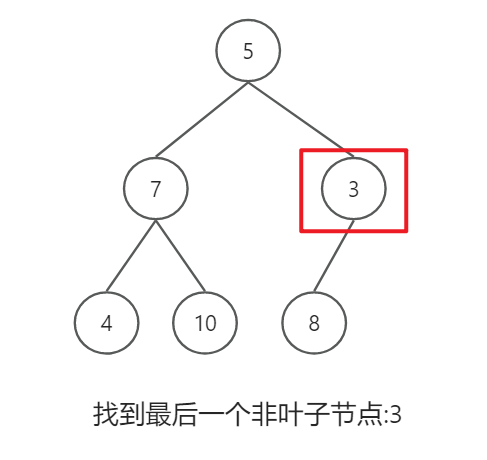
- 找到最后一个子树(最后一个非叶子节点),调整为根元素最大的子树
- 从后往前,将每个子树调整为根元素最大的子树
- 若当前子树发生了变化,则还要从上到下检查他的子树是否需要改变
有点像冒泡排序上浮的思想,从最后一个子树开始,将最大的元素慢慢上浮到顶端
那么如何求得最后一个子树的位置?
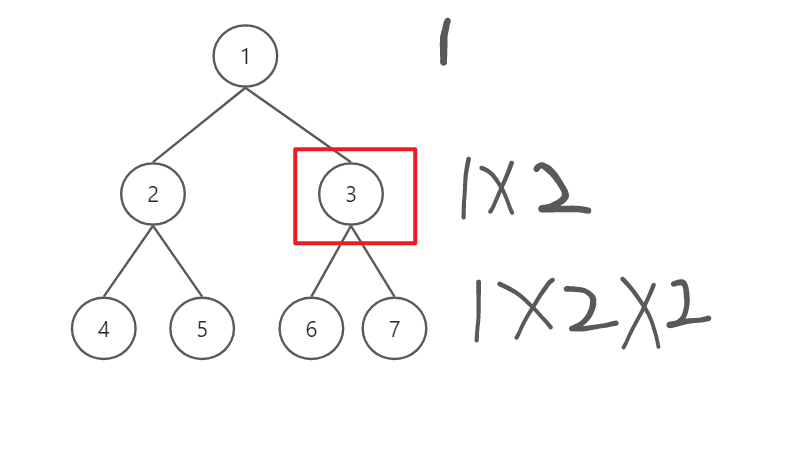
完全二叉树(满二叉树):
由图可知,最后一个非叶子节点应该是3,通过性质可知最后一层之上的所有结点数+1等于最后一层结点数,由此可得最后一个非叶子节点索引应该是len/2 - 1
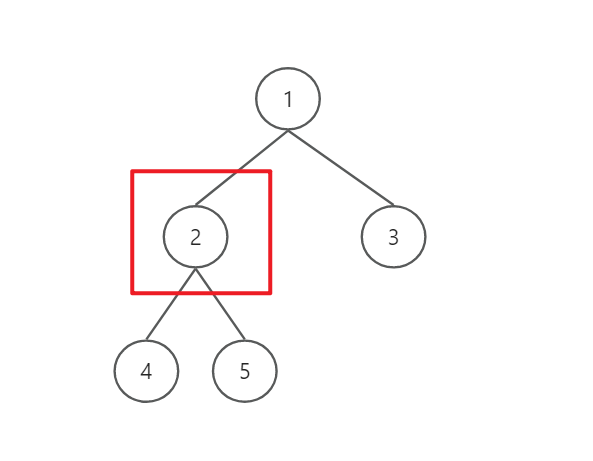
完全二叉树(非满二叉树):
由图可知,由于完全二叉树的性质,将所有子节点都聚集在左侧,因此非满二叉树的第一个非叶子节点索引依旧是len/2 - 1
找到最后一个子树后,每个子树的操作应该是: 判断当前子树的根节点是否是最大的(即比左右节点中的最大值大),若是则直接跳过,不是则交换
代码如下:
public void HeapToBig(int[] arr, int start, int end)
{
int tmp = arr[start];
for (int i = 2 * start + 1; i <= end; i = i * 2 + 1) //i从初始的start子树中的左节点开始,并遍历它的子树
{
//i<end是保证不会下标越界
if (i < end && arr[i] < arr[i + 1])//保证i一定是左右节点中最大值的下标
{
i++;
}
if (arr[i] > tmp) //start中的值始终都是最初start元素的下标
{
arr[start] = arr[i];
start = i;
}
else //若满足条件,则可以直接退出
{
break;
}
}
arr[start] = tmp;
}
public void HeapSort(int[] arr, int len) //len为arr.length
{
//首先将乱序数组调成大根堆,从后往前调整
//这里i--的原因是,len/2 - 1是最后一个子树,前面的元素都会是一个子树的根节点
for(int i=(len-1)/2;i>=0;i--)
{
HeapAdjust(arr, i, len - 1);
}
//每次将根和待排序的最后一个交换,然后再调整
int tmp;
for (int i = 0; i < len - 1; i++)
{
tmp = arr[0];//将堆顶和最后一个位置交换
arr[0] = arr[len - 1-i];
arr[len - 1 - i] = tmp;
HeapAdjust(arr, 0, len - 1 - i- 1);//end为原长度-已排好序长度
}
}举例:
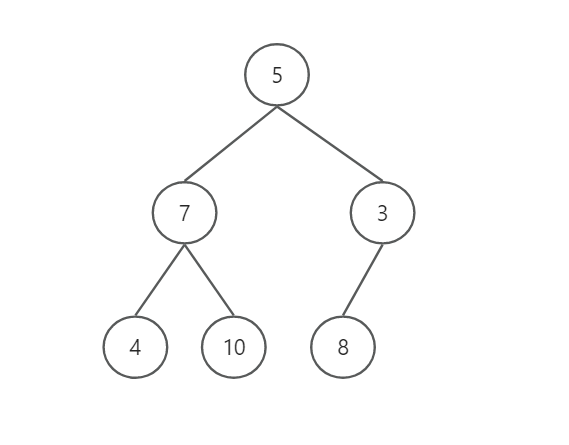
使用堆排序将数组[5,7,3,4,10,8]进行升序排序
将乱序数组变为大根堆
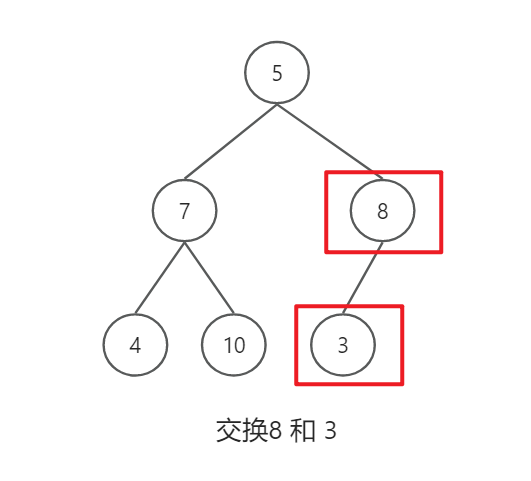
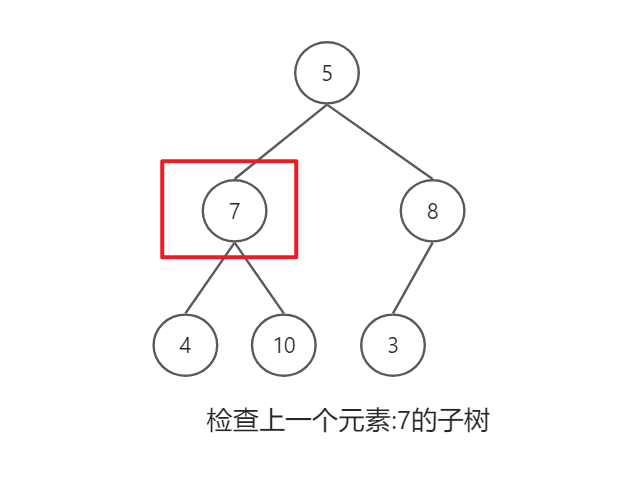
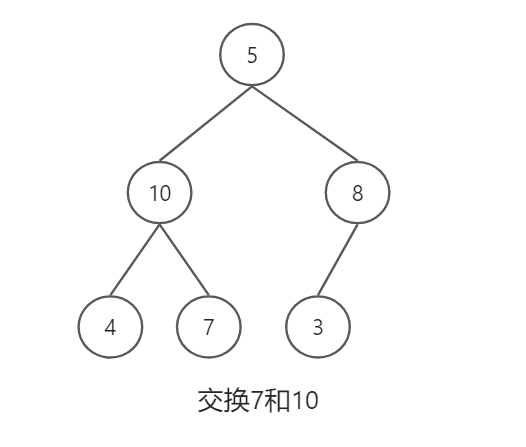
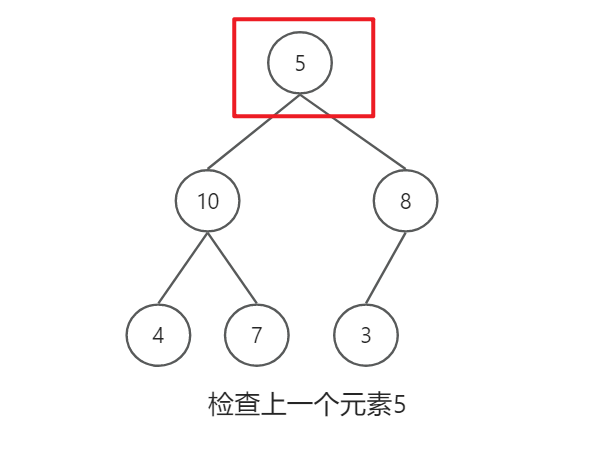
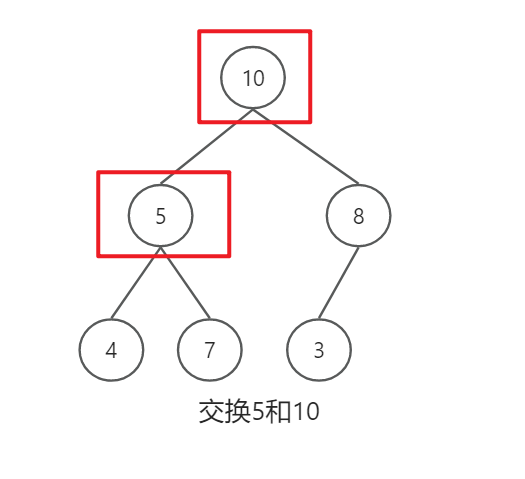
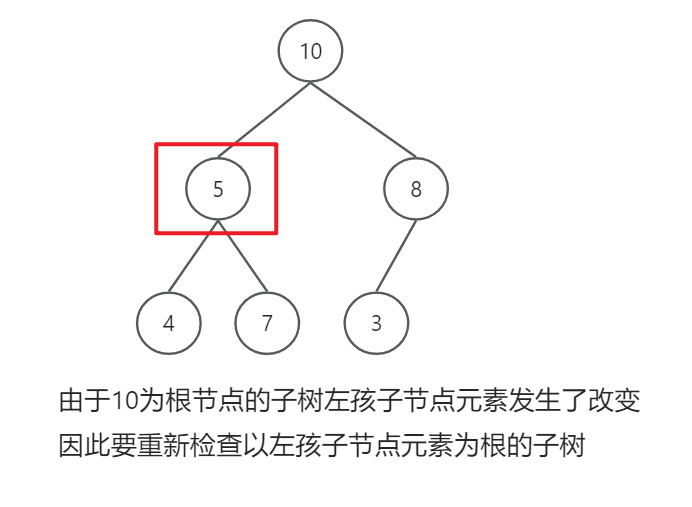
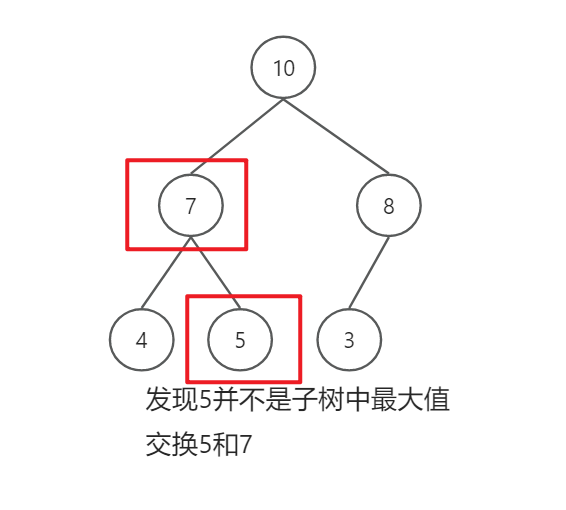
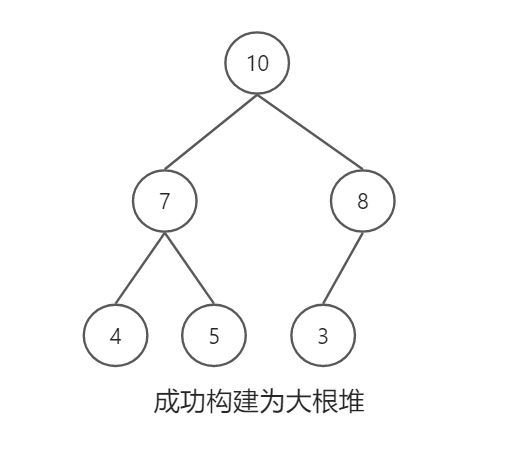






















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








