【两次过】Lintcode 701. 修剪二叉搜索树

最新推荐文章于 2025-05-26 02:30:00 发布

原创最新推荐文章于 2025-05-26 02:30:00 发布 · 196 阅读

0 ·

CC 4.0 BY-SA版权

lintcode 同时被 2 个专栏收录

393 篇文章

订阅专栏

二叉树

67 篇文章

订阅专栏

本文介绍了一种算法，用于修剪二分搜索树，使其所有节点的值位于指定的最小值和最大值之间，同时保持树的二分搜索特性。通过递归地检查每个节点，并修剪不符合条件的子树，可以有效地完成这一任务。

给定一个有根的二分搜索树和两个数字min和max，修整这个树使得所有的数字在这个新的树种都是在min和max之间（包括min和max）。然后这个所得的树仍然是合法的二分搜索树。举个例子，输入是: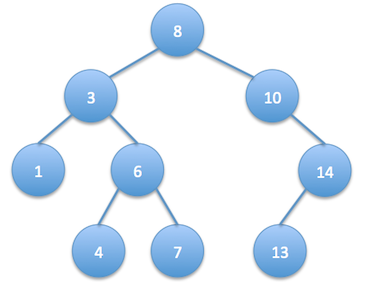

然后我们给定min为5和max为13，这样得到的二分搜索树的结果应该是：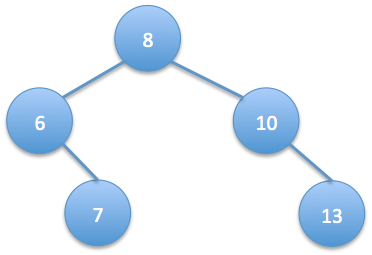

样例

样例1

输入：
{8,3,10,1,6,#,14,#,#,4,7,13}
5
13
输出： {8, 6, 10, #, 7, #, 13}
说明：树的图片在题面描述里已经给出

样例2

输入：
{1,0,2}
1
2
输出： {1,#,2}
说明:
输入是
  1
 / \
0   2
输出是
  1
   \
    2

解题思路：

分治法。若根节点的值小于最小值，则递归调用右子树并返回右子树；
若根节点的值大于最大值，则递归调用左子树并返回左子树；
否则修剪左子树，右子树并返回根节点。

/**
 * Definition of TreeNode:
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left, right;
 *     public TreeNode(int val) {
 *         this.val = val;
 *         this.left = this.right = null;
 *     }
 * }
 */

public class Solution {
    /**
     * @param root: given BST
     * @param minimum: the lower limit
     * @param maximum: the upper limit
     * @return: the root of the new tree 
     */
    public TreeNode trimBST(TreeNode root, int minimum, int maximum) {
        // write your code here
        if(root == null)
            return null;
        
        if(root.val < minimum)
            return trimBST(root.right, minimum, maximum);
        if(root.val > maximum)
            return trimBST(root.left, minimum, maximum);
        
        root.left = trimBST(root.left, minimum, maximum);
        root.right = trimBST(root.right, minimum, maximum);
        
        return root;
    }
}