[Leetcode] 407. Trapping Rain Water II 解题报告

题目：

Given an m x n matrix of positive integers representing the height of each unit cell in a 2D elevation map, compute the volume of water it is able to trap after raining.

Note:
Both m and n are less than 110. The height of each unit cell is greater than 0 and is less than 20,000.

Example:

Given the following 3x6 height map:
[
  [1,4,3,1,3,2],
  [3,2,1,3,2,4],
  [2,3,3,2,3,1]
]

Return 4.

The above image represents the elevation map [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] before the rain.

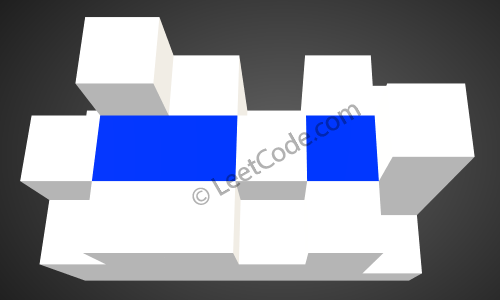
After the rain, water are trapped between the blocks. The total volume of water trapped is 4.

思路：

我记得Leetcode中好像有Trapping Rain Water I这道题目，我也贴出来解题报告了。其实这道题目就是将一维的情况扩展到了二维上，但是基本思路还是一样的：在一维中我们只需要从两个端点中选一个较低者即可，而在二维中可选的点就扩大成了整个矩形的四个边。根据上一道题目知道，我们每次应该先选取边界最小的高度，所以很自然的可以想到优先队列或者小顶堆来保存周围边界。在我们访问过了一个点之后，要继续在矩形的内部遍历，所以还需要保存一个点的位置信息（注意下面的代码将二维位置信息映射到了一维上）。为了防止再次访问已经访问过的点，还需要用一个数组来标记每个点的访问状态。

由于优先队列中的元素个数可达m*n个，所以该算法的时间复杂度应该是O(m*n*log(m*n))，空间复杂度是O(m*n)。

代码：

class Solution {
public:
    int trapRainWater(vector<vector<int>>& heightMap) {
        if(heightMap.size() == 0) {
            return 0; 
        }
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> que;    // smallest height in front
        int row = heightMap.size(), col = heightMap[0].size();  
        vector<vector<int>> visited(row, vector<int>(col, 0));
        int ans = 0, Max = INT_MIN;  
        for(int i = 0; i < row; i++) {  
            for(int j = 0; j < col; j++) {  
                if(!(i == 0 || i == row - 1 || j == 0 || j == col - 1)) {   // boundary grid
                    continue; 
                }
                que.push(make_pair(heightMap[i][j], i * col + j));          // put all the bounary grid in the que
                visited[i][j] = 1;
            }  
        }  
        vector<vector<int>> dir{{1, 0}, {-1, 0}, {0, 1}, {0, -1}};  
        while(!que.empty()) {  
            auto val = que.top(); 
            que.pop();  
            int height = val.first, x = val.second / col, y = val.second % col;
            Max = max(Max, height);     
            for(auto d: dir) {      // for each direction
                int x2 = x + d[0], y2 = y + d[1];  
                if(x2 >= row || x2 < 0 || y2 < 0 || y2 >= col || visited[x2][y2]) {
                    continue;
                }
                visited[x2][y2] = 1;  
                if(heightMap[x2][y2] < Max) {
                    ans += (Max - heightMap[x2][y2]);  
                }
                que.push(make_pair(heightMap[x2][y2], x2 * col + y2));
            }  
        }  
        return ans;  
    }
};