求 1/1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 + 1/7 - 1/8 + ... 1/100的值

使用两种方法对此题求解：

人之所以痛苦，那是因为在成长。 -------magic_guo

for 循环方法和while循环方法：
话不多说，直接上代码：
for循环方法：

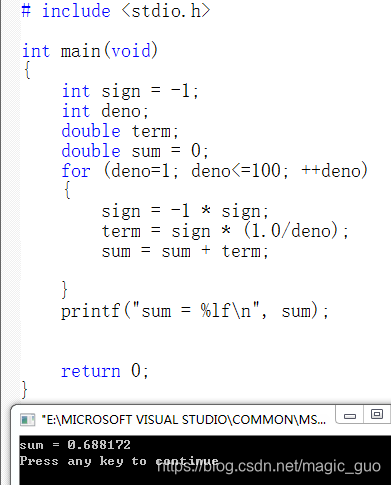
while循环方法：

题解分析：
① 第一项的分子分母都是1
② 第二项的分母是2，以后每一项的分母都是前一项的分母加1
③ 第二项前的运算符为负，后一项的运算符都与前一项的运算符相反

思路：
S1：sign = -1 代表每一项的符号
S2：sum = 0 代表总和
S3：deno = 1 代表当前项的分母
S4：sign = (-1) * (sign) 每一项的符号都会变
S5：term = sign * (1.0/deno) 代表当前项的值
注意：定义term 和 sum 时，要定义为浮点型，无论float或者double都行。
S6：sum = sum + term 计算全部的值
S7：deno = deno + 1 每一次都要将deno（分母）加1
S8：若deno <= 100，返回S4，否则算法结束。

虽说此题为都100的和，大家可以灵活运用，求n项的和，只用将100改为n即可。