为什么织好的毛衣不会散架？科学家也刚知道是怎么回事-优快云博客

真是细节大家应该还对去年奥运会上英国跳水名将汤姆·戴利在观众席上边看比赛边打毛衣的画面记忆犹新吧。

只见这位奥运冠军心无旁骛、技法纯熟地摆弄着毛线针和紫色毛线，隔着屏幕都能感受到他身上的一丝贤惠。
‍

他还在采访中表示，这次来参加奥运会，最怕的不是拿不到金牌，而是没带够毛线。

作为人们生活中常见的一类衣物——毛衣，可以说是大家冬天的御寒神器之一。‍‍‍‍‍‍

一件柔软且回弹性好的毛衣，不论是内搭还是外穿，都是冬季穿搭的一个“万能钥匙”。而且，一件织好的毛衣，不论你怎么拉扯揉搓，基本不会发生太大的变形、损坏甚至散架，可以说是非常耐造和实用了！

那么，问题来了，为什么织好的毛衣不会散架呢？科学家们最近发现了其中奥秘。这其中涉及到我们生活中常见的摩擦力以及物质的态等问题，今天我们就来聊一聊毛衣里的那些事。

无处不在的摩擦力

提到摩擦力，大家肯定都不陌生，它不仅出现在了我们初高中时期的物理课本上，也在我们每天的生活中扮演着重要角色。在走路、汽车、拧瓶盖等各种生活场景中，我们都离不开摩擦力，如果没有摩擦力，不仅鞋带系不紧，就连筷子都没了用武之地。

摩擦力分为静摩擦力、滚动摩擦力和滑动摩擦力。当两个接触面粗糙的物体之间有压力，并且有相对运动趋势的时候，就会产生静摩擦力。当这两个物体之间发生相对运动时，静摩擦力就转变成动摩擦力，这就是我们熟知的库仑摩擦定律。

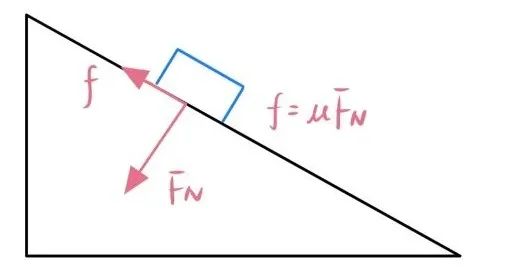
滑动摩擦力的大小与接触面间的压力和接触面的粗糙程度成正比。用公式表示为：

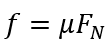
最大静摩擦力一般大于滑动摩擦力。

滚动摩擦力是一个物体在另一个物体上面滚动时产生的摩擦力，滚动摩擦力实际上是一种静摩擦力。例如，放在斜面上的小球，在小球向下滚动过程中，小球与斜面的接触点一直在改变，而每个接触点与斜面之间都是静摩擦力。

这么看起来摩擦力好像总是充当阻力的角色，但是实际上，很多时候正是摩擦力提供了物体向前运动的力。

例如，我们行走的时候，用力向后蹬地，脚与地面之间的静摩擦力就提供了前进的动力；骑自行车的时候，车轮与地面之间的滚动摩擦力也提供了向前的动力。

再比如，我们平时系鞋带的时候，可以打一个平结，并且结中间的鞋带最好扭一下，更不容易散开哦！这是因为平结鞋带比顺结鞋带末端的甩动幅度要小，而且结上的鞋带还扭了一下，所以摩擦力更大，也就不容易散开。

生活中常用的打结方法，左图是顺结，右图是平结

平结上扭一下的地方，可以增加摩擦力，让鞋带不容易松开

全局是稳定还是不稳定？

在地上堆一个沙堆时，缓慢地从上方添加颗粒，沙堆逐渐增高，其倾角θ会越来越大，当超过某一角度θₘ时，沙堆开始崩塌。沙堆的倾角迅速减小到θᵣ时，崩塌停止。那么，这个沙堆到底是稳定还是不稳定呢？我们可以发现，沙堆问题中存在一个明显的阈值θₘ，当低于阈值时，沙堆稳定，否则沙堆开始崩塌，这就是亚稳态。

在物理中，亚稳态是指一种系统处于局部稳定的状态，但它并不是全局最稳定的状态（最低能量状态）。系统在亚稳态中可能会保持一段时间，只有当受到足够的扰动（如外力、热扰动）时，系统才会跳到更稳定的状态。从势能图中，我们可以更进一步认识亚稳态的概念。

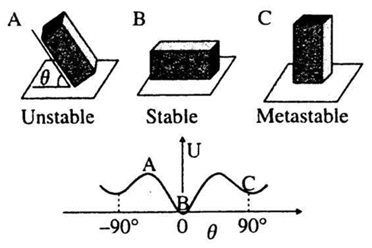
稳态、亚稳态和非稳态

而在自然界中，亚稳态也非常常见，例如过冷液体、超导态、原子的激发态等。

过冷是指一种液体被冷却到其正常凝固温度以下但仍保持液态的现象，它是一种亚稳态现象，在过冷状态下，液体并没有结晶形成固态，只有当有足够的外界扰动（如振动或加入杂质）时，液体才会跳跃出亚稳态，从液体跃迁到固态（也就是稳态）。

“滴水成冰”就是一个典型的过冷现象

织好的毛衣为什么不会散架？

首先，我们得重新认识一下什么毛衣，一件编织手艺复杂的毛衣它的基本结构又有哪些呢？

毛衣其实本质上算是针织物。针织物在成形时是通过织针有规律的运动将经向或者纬向送入的纱线依次弯曲成圈，再将前后生成的线圈相互串套起来形成的。简单来说，就是把纱线变成线圈，然后把线圈串套链接起来。

因此，可以把线圈作为针织物的基本结构单位，每个线圈是由圈干1-2-3-4-5 和沉降弧5-6-7 组成的，圈干又分为上部曲线部分的针编弧2-3-4 和两个侧面直线部分的圈柱1-2 和 4-5。

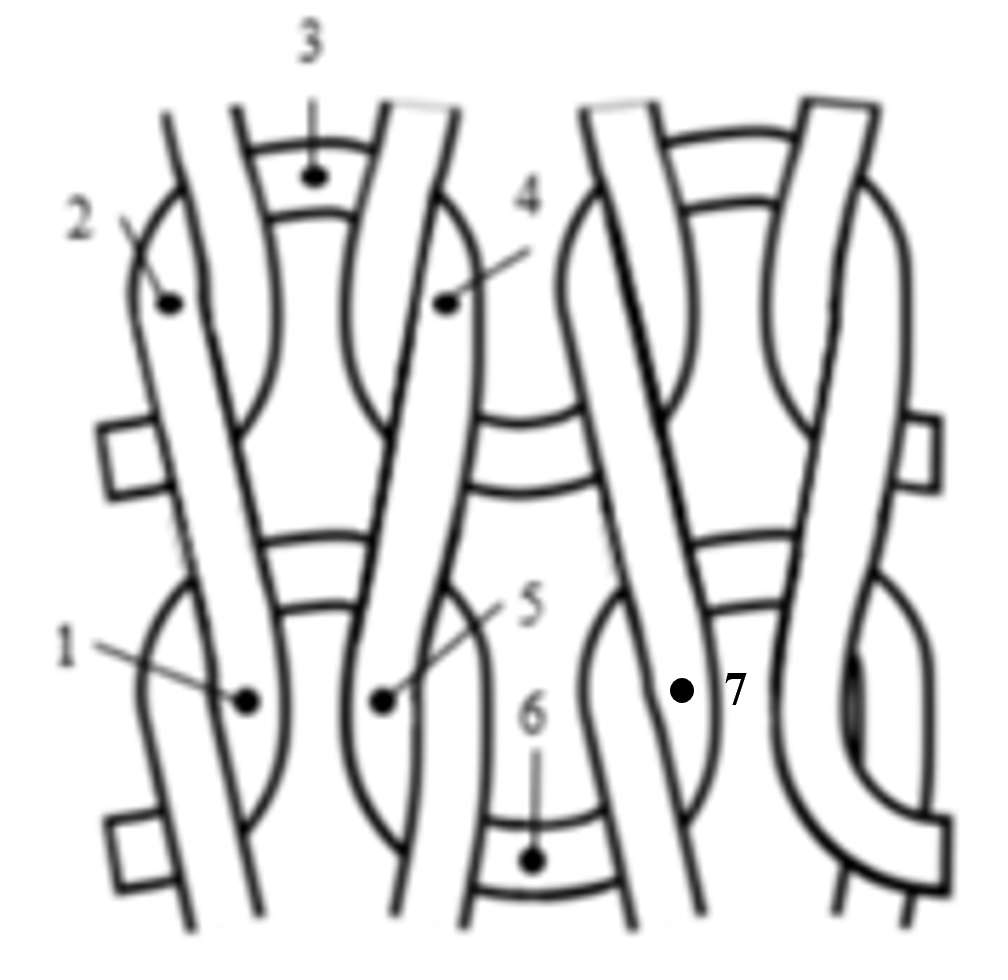
针织物线圈结构

根据编织方向的不同，针织物又可分为纬编和经编两种类型，纬编针织物在线圈成形时是沿织物横向依次进行的，而经编织物则将纱线沿织物纵向垫入同时成圈。

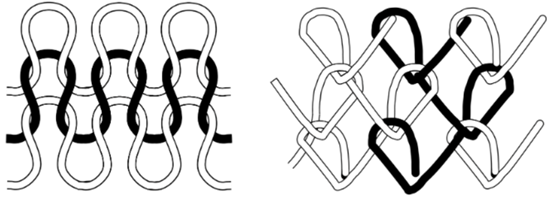
纬编针织物结构图和经编针织物结构图

而在外观上，线圈也有正反之分，圈柱位于其所穿套线圈的针编弧与沉降弧之上的线圈称为正面线圈（圈柱压着圈弧的一面），反之若针圈柱被针编弧与沉降弧所覆盖则称该线圈为反面线圈（圈弧压着圈柱的一面）。

正面

反面

相比其他织物，纬编针织物独特的线圈结构使其具有更好的弹性、延展性、透气性和柔软度，被广泛用于服装、家具纺织品等行业。那么，我们接下来就以纬编的线圈为例。

我们将视角集中在一个个纬编线圈的上，每一条纱线的直径为d，长度为l，这些线圈相互套住，形成环环相扣的网络结构，像锁链一样，每个线圈都与其他线圈交织，支撑着整个结构。而毛衣这类针织物一般由纱线或者羊毛等材质制成，每一个交织的线圈之间都存在摩擦力。

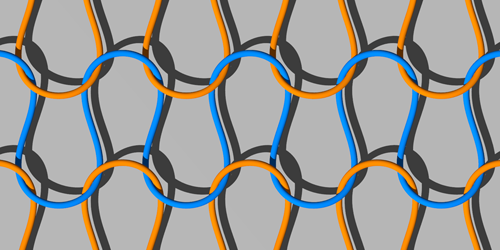
环环相扣的毛衣“网络”

接下来我们就对线圈交织处进行受力分析，当线圈网发生稳定变形时，交织中的纱线发生滑动，此时摩擦力转为滑动摩擦力。根据库仑摩擦定律，切向摩擦力f_ξ^(t)与法向接触力 f_ξ⁽ⁿ⁾之间的关系为：

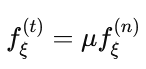
其中，μ为摩擦系数。

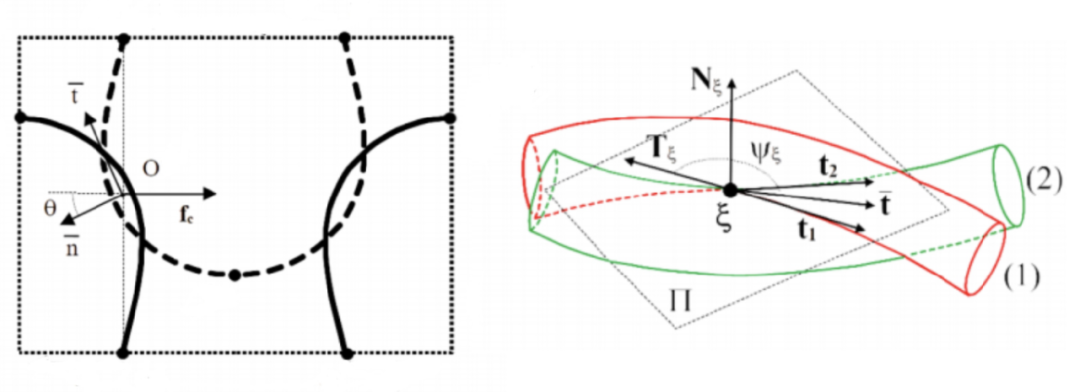
对于两个相交织的纱线1和2来说，虽然实际上存在两个接触点，但是O点中心线之间的距离通常为：1.03d ≈ d，而接触点之间的距离远小于纱线长度l，因此我们可以将两个接触点简化成唯一的接触点O。

在接触点处，出现了法向接触力N_ξ和切向接触力T_ξ，法向接触力垂直于纱线在接触点的切向矢量t_i：

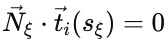
而切向接触力可以写成：

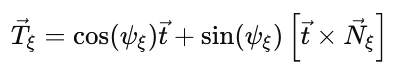
其中，ψ_ξ描述切向接触力和t之间的夹角。

根据接触力的平衡条件，可以得到总接触力f_c：

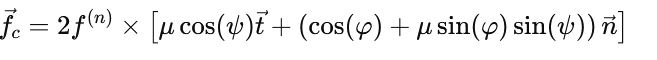
编织倾角tan(θ)：

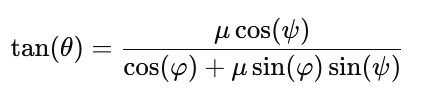
其中，ψ 是接触点切向接触力方向与编织轴方向(t)之间的夹角，φ 是接触点法向力方向(N_ξ)与参考平面的夹角。因此，可以看出编织倾角由摩擦系数μ和几何参数ψ、φ共同决定。

一个月前，Jerôme等人^[1]通过简单的实验验证，他们发现：编织倾角决定纱线的排列紧密程度，影响编织材料的几何和力学性能，并且确保结构的力学平衡和几何稳定性。倾角的变化限制了纱线的滑动和摩擦行为，从而确保结构的稳定性。

同时他们通过实验验证，在无外力的情况下，线圈的摩擦力会导致毛衣处于一系列的亚稳态，这里我们简单介绍产生亚稳态的影响因素：

(1) 摩擦力的限制作用：根据库仑摩擦定律，摩擦力 f ≤ μN 限制了纱线之间的滑动，摩擦力在接触点提供了“势垒”，阻止纱线轻易离开当前排列，形成一种“卡住”的效果。

(2) 几何约束：编织结构中的纱线通过交织形成空间上的几何约束，例如交叉点和线圈的形状，几何约束增加了系统能量势垒，使纱线更难滑动到全局稳态。

(3) 能量耗散：在纱线调整过程中，滑动摩擦会将一部分动能转化为热能，从而降低系统的总能量，动能的减少使纱线无法逃离当前局部能量谷，从而停留在亚稳态。

可以发现，处于一系列亚稳态的毛衣，即使出现了外力拉伸和压缩，毛衣受到扰动会进入其他的亚稳态，从而不容易散架。

用量子纠缠编织空间

除了用纱线编织毛衣，科学家们还用量子纠缠编织时空，纠缠是一种纯粹的量子现象。处于量子纠缠中的粒子，无论相隔多远，当其中一个粒子的状态发生变化，另一个将立刻受到影响。这种强烈的相关性似乎超越了空间和时间，例如，一旦知道一个粒子的自旋，就能马上确定另一个粒子的自旋。也许，正是基本粒子之间的这种深层量子联系将空间和时间连接在了一起。

研究发现所需要的纠缠几何形成树状结构，其中每对纠缠的原子都与另一对纠缠在一起，这种单独的、低层次的纠缠最终构建成一个完全纠缠的系统，进而产生时空体空间。

所以说生活中处处有物理呢！

话已至此，小编也想起了，小时候晚上写作业的台灯下，陪伴在一旁的妈妈手里拿着的不是手机，而是上下翻飞的毛衣针。现在就尝试织一件毛衣送给妈妈\(^o^)/

参考文献：

[1] Crassous J, Poincloux S, Steinberger A. Metastability of a Periodic Network of Threads: Shapes of a Knitted Fabric[J]. Physical Review Letters, 2024, 133(24): 248201.
[2] Daily-Diamond C A, Gregg C E, O'Reilly O M. The roles of impact and inertia in the failure of a shoelace knot[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2017, 473(2200): 20160770.
[3]汤炜.纬编针织物组织结构识别方法研究[D].浙江理工大学,2023.

编辑：悦悦

我们是谁：

MatheMagician，中文“数学魔术师”，原指用数学设计魔术的魔术师和数学家。既取其用数学来变魔术的本义，也取像魔术一样玩数学的意思。文章内容涵盖互联网，计算机，统计，算法，NLP等前沿的数学及应用领域；也包括魔术思想，流程鉴赏等魔术内容；以及结合二者的数学魔术分享，还有一些思辨性的谈天说地的随笔。希望你能和我一起，既能感性思考又保持理性思维，享受人生乐趣。欢迎扫码关注和在文末或公众号留言与我交流！