对称思维的妙用之从解题到本质（五）——挑战网红题之鸭子半圆概率问题-优快云博客

本文链接：https://blog.youkuaiyun.com/magic2728/article/details/129630915

文章通过一个鸭子在半圆内概率的问题，探讨了对称思维在解决数学问题中的应用，强调了直观理解与数学证明的结合。作者分享了错误解答的经验，指出了解题过程中对称性、独立性和互斥性的数学思想，并展示了如何通过极坐标简化问题，但同时也指出在处理复杂情况时需要更巧妙的建模方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

早点关注我，精彩不错过！

在前面的文章中，我们从对称的案例到原理到套路，又回到题目，彻底理解了对称思维在解数学题中的用法。相关内容请戳：

对称思维的妙用之从解题到本质（四）——用三个套路秒杀一众问题

对称思维的妙用之从解题到本质（三）——三个套路总结

对称思维的妙用之从解题到本质（二）——斗地主中有人抓到王炸的概率是多少？

对称思维的妙用之从解题到本质（一）——巴格拉斯效果发生的概率

但是，促使我写这个系列文章的，其实并不是前面这些题，而是三年多前刚疫情开启过年那会，王志伟老师给我发来的一个题目，我当下就给出了错误的解答，并且一度不知情。直到很长时间过去，这题居然成了网红题，被各种疯狂转发，我再度思考它时，才发现我思维上的漏洞，因此才有了以上这个系列。并且，除了这些逻辑就能思考出来的方法，这题的多思路解法也让我不禁想与你分享一番。

鸭子半圆概率问题分析

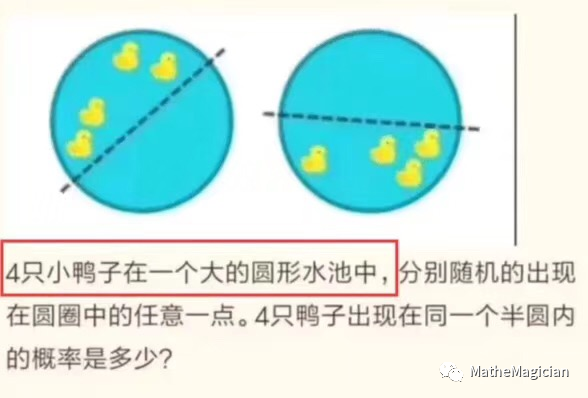
其实答案并不难。感性一点的理解可以这么做：选取其中1只鸭子作为半圆的逆时针圆弧轨迹的起点，那么剩下鸭子是否在这个半圆内的概率都是1 / 2，因位置互相独立，故都在的概率为1 / 2 ^ (n - 1)。而每只鸭子都可以作为选取圆弧的起点，因此是n / 2 ^ (n - 1)，n = 4时，答案是1 / 2。

说到这里，可能小学奥数班的孩子们大体也能理解，并似懂非懂地记忆下了这个过程，可能有类似的问题还能接着套用。可是，以上地解释并不是完全的数学推导，要证明其正确性，还有很多功课需要补足。只是我们愿意相信我们的直觉，且在简单问题上，这些直觉往往还真就是正确的。奥数班给了孩子们思考的机会，可是是否真的抓住机会学透了，就看自身的修为了。

实际上，要完成本题完全数学上形式化的解析，需要非常巧妙地找到建模方法，以及综合应用分类，对称，独立，互斥，等价等诸多数学思想。而形式化表达成这样的思路来源，还是源自对问题本身特点的剖析。

抛去实际背景，本题的纯数学问题为：给定一个圆o以及其内4个点o1~o4，求4个点处在一个半圆内的概率。

如果不考虑针对解决问题的建模方法，此题的解法会推向另一个死板的极端：4个点就是4个平面坐标，各自服从单位圆内的均匀分布，互相独立，这里就有8个自由变量了。然后在一个半圆内，应该是描述为，存在一条有方向的直径（0~2pi），所有的点都在其右手系的半圆内（四指从直径方向转向视线方向，大拇指指向的方向内的半圆），这又是一个自由度。因此，配合上古典概型，这么个简单的问题就变成了一个有9个自由度的微积分问题。因为半圆只是存在就算数，表达式里就会有个奇怪的只要存在值就为1的式子，然后对这个函数在4个平面点的平面内积分……

当然没有人会这么求，我只是举个极端的例子来说明，把数学读傻，而没有一点灵动性的后果，而且这种方法完全没法拓展到n只鸭子的情况才是最致命的。实际上，我们可以发现很多数学性质来转化和化简我们的问题。以上是真的不用任何性质，纯粹把题意直接翻译成数学语言的结果，有些夸张了。但是能否找到最合适的结构，并且能严谨地抵达，既没有想当然的错误，解法也足够简洁，还是需要一番功夫的。

首先，我们采用极坐标来表达鸭子的位置。显然鸭子坐标中的极半径是对结论没有影响的。即，4只鸭子是否出现在同一个指定的半圆内与否情况关于其鸭子极半径变化对称，或者说该结论关心的变量是半径变化函数的不动点。因此顺带的存在这样的半圆，求概率等，就都关于极半径变化对称了。因此，4只鸭子其实仅需要考虑4个角度的自由度就够了。

另外，4只鸭子的题设要求的这个性质，是这些鸭子的集合的性质，我们知道集合的无序性，用集合的话说就是，集合对序列顺序变化的置换操作对称。因此，我们可以给鸭子的编号1，2，3，4，也不失一般性。这里“不失一般性”，说的就是，怎么编号都是这个集合，所以，我们可以用其中的任意一个来代表。

接下来这一步和上面的扑克牌问题有点像，我们可以比较一下异同。相同的部分是，鸭子子在泳池中的角度位置，和Joker在扑克牌叠的位置是等价的。只不过，扑克牌叠是离散序列，这里是连续取值。离散序列的每个元素是要占空间，有质量的，而连续的则是不占地方的质点模型。还有一个根本的不同，就是这里是存在半圆，而那里是随意取了三份，问其中是否存在一个。前者的自由度是整个角度，而后者仅仅是3个选一个而已；后者被等效成了含有大王的那一份，以去掉了这个自由度来化简，那鸭子水池问题中的这个半圆选取的自由度怎么去除呢？核心仍然是对称性，也即某种不变性。接下来我们具体解释一下，为什么可以如本题开头那样来解析。

问题的关键在于我们怎样不重复不遗漏地选择半圆。即把所谓数学上的存在，等价为真的一系列的半圆类型，并且满足不重不漏，也就是能够符合加法原理，或者说是互斥事件的相加公式。

自然我们可以以编号为1的点开始，然后再以劣弧（半圆弧度以内）找点2，显然它们一定在一个半圆内（当二者构成直径，规定以直径方向斜率为正的半圆为所求），而且可以由此约定目标半圆即为起点开始的180度范围。剩下两个点3和4处在这个半圆的概率是1 / 2 ^ (n - 2)，即为所求。

等等，好像和最前面给的答案不一样？难道标准答案不对，或者，你能指出这个解法的问题吗？

问题在于，我们求得的解确实满足题意，可是一定还漏掉的一些解。比如我们的1,2号点，完全也可以处在一个以2位起点的半圆弧上，那样某些上述不包括的情况就也满足题意了。

那能这样分类再加上吗？也不行。因为这一个以1还是2作为半圆起点或终点的划分方案的两个圆弧是有它们之间那段劣弧的重合的，即当一个点处在中间的时候，会被算两次，而这完全取决于两个点之间弧度的大小。这使得这些不互斥的事件根本没法相加，自然也没法用乘法简便计算了。为了算清楚，又必须要引入微积分了。

也就是说，我们没能构造对解决问题有利的对称过程（一只鸭子一只鸭子依次分析的），以在对称对立分类的基础上简化相乘。这个构造过程要重来，并且做到不重复，不遗漏，还能简化计算得了。

在给出更优的计算过程之前，为了提示思路，也为了完整性，不妨给大家展示一下当n比较小时候的计算过程：

鸭子半圆概率问题特例求解

n = 3

前两个点之间以其中一个为0度，另一个为a，范围是[0, pi]，则第3个点要满足条件的角度取值范围是[- pi + a, pi]，由于都是均匀分布，我们只需要对第二个点的角度a积分，第3个点可以直接给出变长积分结果，有：

p = int(0, pi)(pi - (- pi + a) / 2pi)da = 3 / 4

n = 4

同理，不过这里第4个点的取值范围和a, b的值都有关系，对于这样积分上下限变动的问题而言，计算是有些繁琐的，需要大量的分类讨论。不过数形结合一下会很好理解。首先a，b的取值范围是一个六边形，面积是3pi ^ 2，也可以看作是砍掉了两个角的正方形，所以看下来，n = 3情况的概率也是很显然了，那第4个点的位置我们不再考虑，而是跳过去直接计算在这个平面内各点处满足条件的概率，直接积分，也就是这个正多面体的体积即为所求。

首先，原点处代表前3点重合，自然p = 1，而底部六边形其余顶点处，无论是两个pi还是一个0一个pi的地方，加上原点的0，都横跨了一个完整半圆了（取其取到pi端点前的左极限那个半圆，到达以后实际上两侧都符合要求了，但是对积分结果没有影响）。因此，还剩下一半的可能第4点落在这个半圆内的概率为1 / 2。而其他的点的概率，分别受到边界向中间角度压缩过程的影响，是线性过程往(0, 0, 1)集中的，因此，整个概率空间的体积是1 * 4 * pi ^ 2，而对应满足题意的部分是(1 / 2 + 1 / 2 * 1 / 3) * 3 * pi ^ 2，占比是1 / 2，即为所求。

而当n再大到5,6这样的数值的时候，我们的这点微积分巧妙计算的雕虫小技根本不值一提，一般化的解的求解把我们没有对称地进行互斥分类，进而直接用乘法简便运算的弱点暴露无遗。

这些就是我在解这道题时遇到的困惑，强行用高等数学工具是解决了，可是完全看不到作为一个趣味数学题的美感，似乎仍然是没能够构造出足够好的解决问题的对称过程，进而化简。我相信在如此对称的圆上，一定还有巧妙的对称性能够直接跳过这些复杂无用的微积分来把问题解决，那具体怎么解呢？

所以我们还得找到存在半圆的等效表达，以及真正能够互斥划分的方法来化简计算。

核心思路还是前面总结的套路：构造对解决问题有利的对称过程，以在对称对立分类的基础上简化相乘。

那到底怎样划分才是对称又对立的分类呢？

我们下回揭晓。

我们是谁：

MatheMagician，中文“数学魔术师”，原指用数学设计魔术的魔术师和数学家。既取其用数学来变魔术的本义，也取像魔术一样玩数学的意思。文章内容涵盖互联网，计算机，统计，算法，NLP等前沿的数学及应用领域；也包括魔术思想，流程鉴赏等魔术内容；以及结合二者的数学魔术分享，还有一些思辨性的谈天说地的随笔。希望你能和我一起，既能感性思考又保持理性思维，享受人生乐趣。欢迎扫码关注和在文末或公众号留言与我交流！