爱学习,勤思考;学数学,玩魔术。欢迎点击头部蓝字关注MatheMagician,这里有你要的奇迹!
答案是肯定的.例如,你可以利用和、积、幂把表示为2+2、2×2、2².如果你喜欢这个数,你也可以用“取上整函数”(不小于该数的最接近的整数)把表示为 ⌈π⌉ .显然存在无穷多种方式来表示,而哪种是最好的,取决于个人喜好.一般来说,你可以用自己最喜欢的方式来表示1到12,从而制作出专属于自己的数学时钟.

如果你想寻找一些独特的东西,你可以使用e、π、i(虚数单位)通过欧拉恒等式来表示:
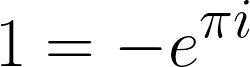
或者,如果你喜欢巴塞尔问题,可以把表示为所有正整数与π的乘积的平方的倒数和的倒数(译者注:原文有误,少了最后的取倒数):
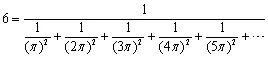
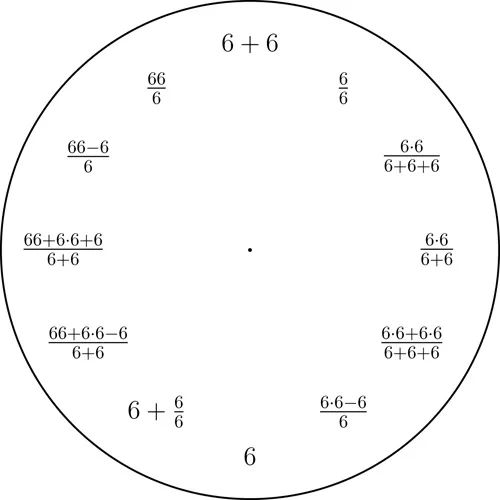
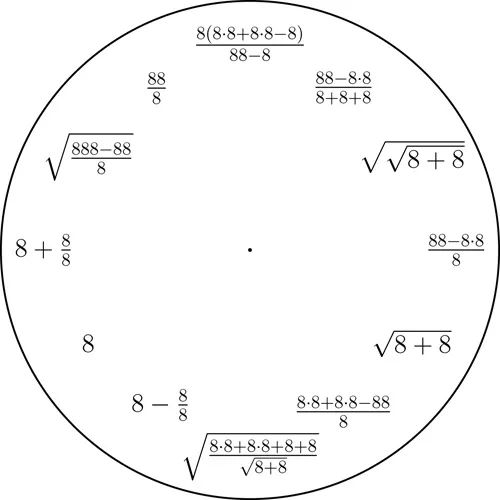
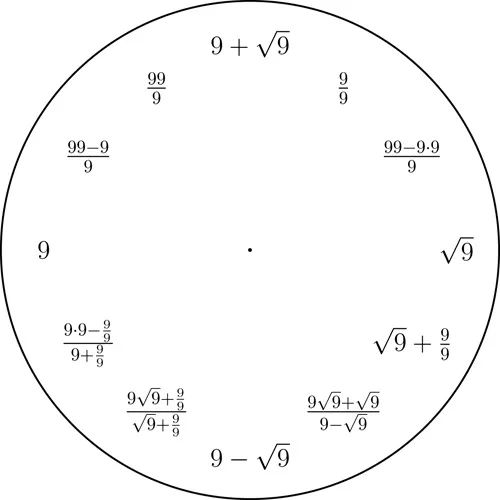
作为一个更具体的例子,你可以从数字1到9中任选一个,然后仅用选定的这一个数字(可以重复使用)和数学符号来表示钟面上所需的所有数字(下面的图中提供了一些示例).
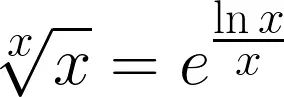
市面上有许多数学时钟,钟面上有着各种各样的表达式.偶尔,你会发现钟面上会有某个数列的前12项,而不是1到12.例如,你可能会碰到前12个斐波那契数:
1,1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144
同样地,你也可以使用字母A到L.
另一种选择是:写下某个方程,使得所要表示的数是该方程的唯一解,例如,把5表示为:
x² + 7 = 10x -18
还有一些数学时钟,钟面上的方程有不止一个解,但恰有一个解在1到12的整数中.一般地,有时数学时钟上是有数学错误的(例如,3并不恰好等于)!
尽管如此,在与数字们相处的过程中,你可以做任何事情来获取乐趣.因此,我们提议你来制作专属于你自己的数学时钟,当然如果你需要一些灵感的话,这里有一些例子.
数学时钟主题
在下面的那些图中,你可以找到各种各样的数学时钟,包括1到12的各种不同的表示法.你可以从中选出一个打印出来,并用它作为钟面(例如,你买一个定制钟面的钟),或者你可以简单地将选定的数字的表达式直接放置在钟面上或周围.你也可以买一些可以直接在钟面上写字的钟,这样你就可以在闲暇的时候更改你的数学时钟.
这里是一些例子:
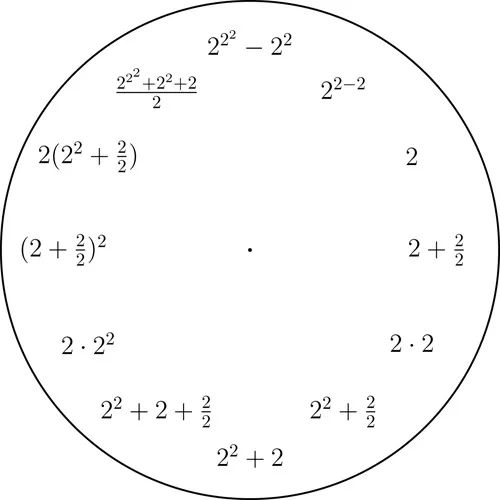
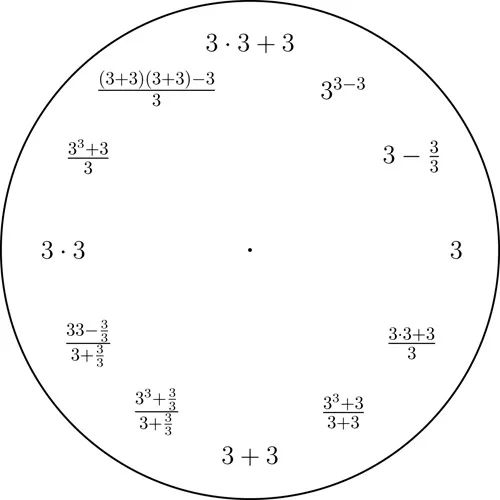
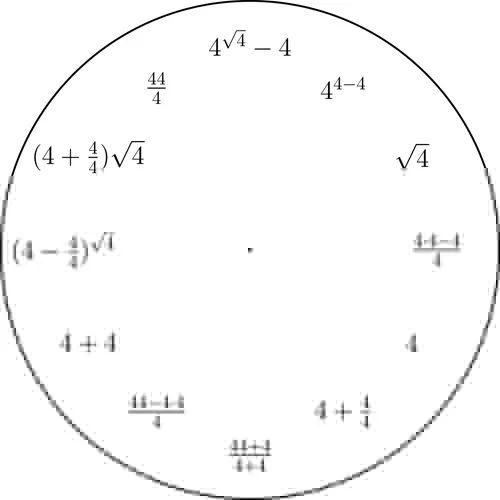
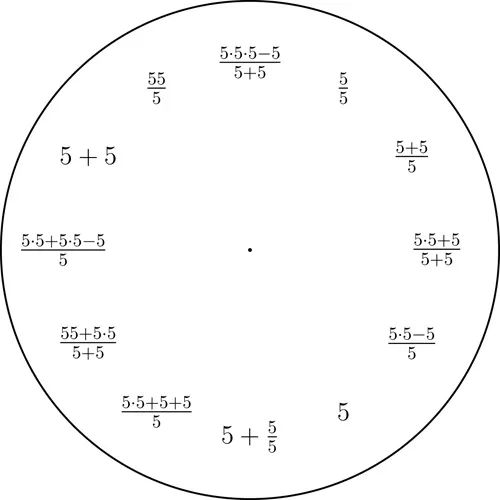
数字1到9的钟
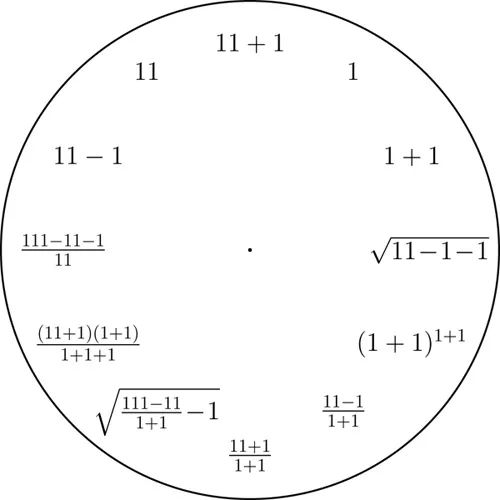
从十进制数字1到9中任意选定一个,然后用只含有选定的那个数字以及算术运算的简短的表达式来表示整数1到12.这里我们使用的是基本的算术运算,以及幂和平方根运算.
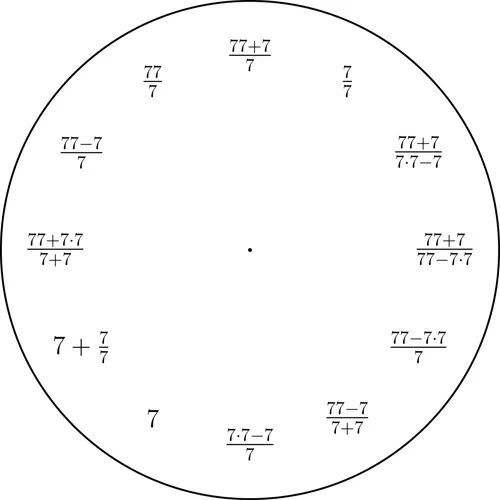
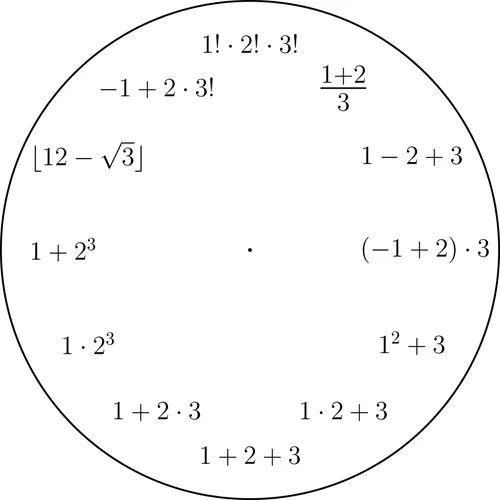
数字1、2、3主题
只可以按照数字1、2、3的次序且每个数字恰好只用一次可以表示整数1到12.这里我们使用基本的算术运算,以及幂、平方根、阶乘运算(正整数n的阶乘,记为n!,定义为从1到n的所有正整数的乘积)和取下整函数 ⌊⌋ (这个函数将一个实数对应到不大于它的最接近的整数).
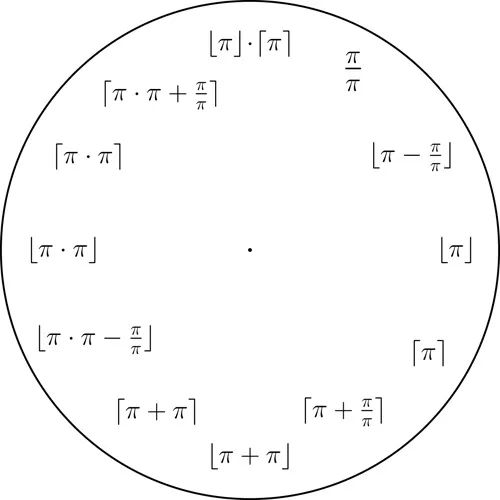
π钟
只使用、基本的算术运算、取下整/取上整函数 ⌈⌉/⌊⌋(这两个函数分别将一个实数对应到不大于/不小于它的最接近的整数)可以表示整数1到12.
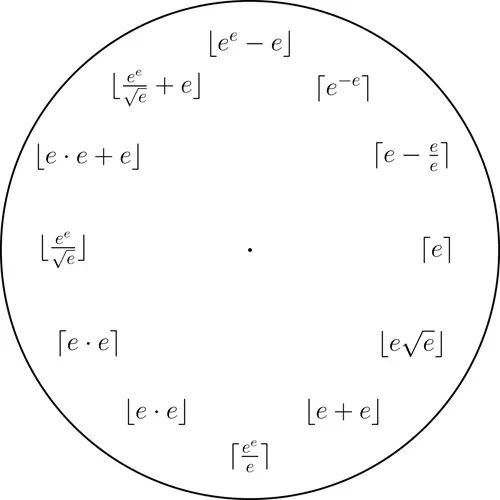
e钟
只使用e、基本算术运算、取幂、取平方根、以及取下整/取上整函数可以表示整数1到12.
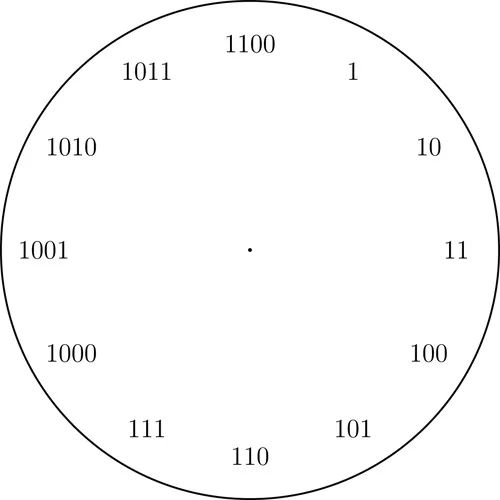
二进制钟
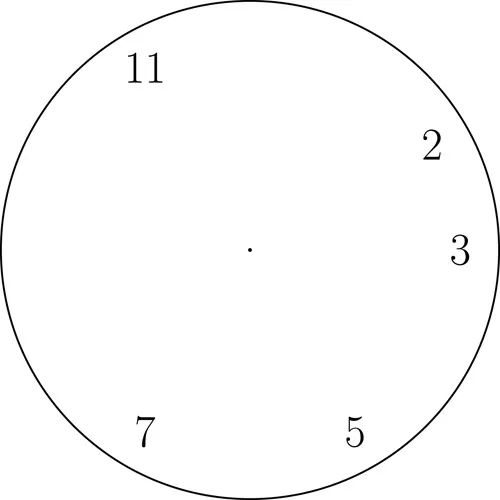
素数钟
在这里,我们只写出1到12中的素数.
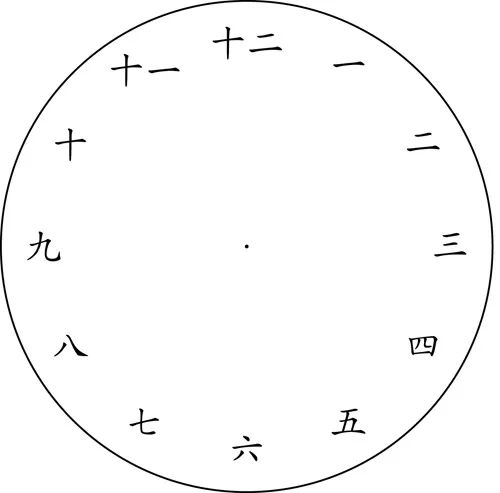
中文数字词钟
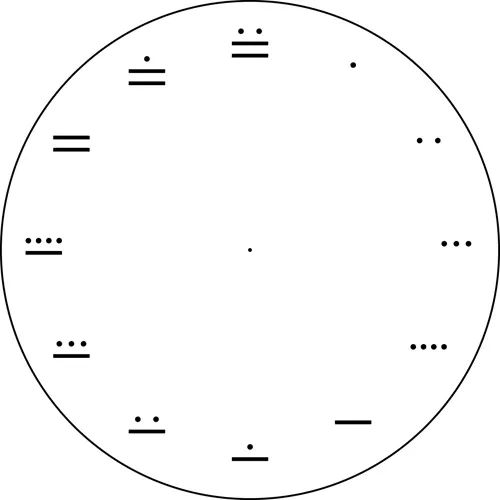
玛雅数字钟
更多的例子...
好了,今天的数学魔术师的分享就到这里,希望各位客官能够喜欢!这里是MatheMagician,有你要的奇迹!
再次感谢各位客官的欣赏,MatheMagician期待您的赞赏哦~
更多精彩内容欢迎扫描下方二维码或点击头部公众号名MatheMagician关注我们,更欢迎把我们的精彩内容奔走相告,我们下期再见!

我们是谁:
MatheMagician,中文“数学魔术师”,是一个十分冷门的职业,原指用喜欢用数学原理设计魔术的魔术师或数学家。但由于数学太过艰深,变成魔术又表演困难,所以这个领域的专业研究者及其罕见。但其实,魔术设计只是数学建模的一个别致的场景;而魔术本身也蕴含着数学之外的诸如心理学,行为科学等其他广阔的议题。我们文章分享的内容涵盖统计,算法,NLP等前沿的数学及应用领域;也包括魔术思想,流程解析,鉴赏等关于魔术的思考;还有大量直接结合二者设计的数学魔术的分享。如果你对数学或者魔术感兴趣,或者喜欢思考和有内涵的文字,我们的内容一定能成为你学习成长的好伙伴!欢迎在文末或公众号留言与我交流!
推荐阅读:





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








