爱学习,勤思考;学数学,玩魔术。欢迎点击头部蓝字关注MatheMagician,这里有你要的奇迹!
写再前面:本系列作品由MathMagician独家首发,一共有七篇,从数学和魔术两个角度对日常生活中“洗牌”这一现象作了挂一漏万的分析。之所以说是挂一漏万,是因为无论数学还是魔术,洗牌中的任何一个小点都够写几篇了。所以,本系列主要选取了一些常见的洗牌方式和相关内容展开作了一些介绍,包括洗牌分类,混乱度评价,过程建模,近似计算,以及几个基本但是及其巧妙的利用洗牌规律设计的魔术。相信聪明的你读完以后,会在数学和魔术上,都对“洗牌”这一现象有着更加深入的认识。
历史文章请戳:
本篇是第三篇:洗牌过程建模
在上一篇文章中,我们介绍了基于熵的关于洗乱的基本定义,还有对于一次洗牌能否洗乱等问题的一个估算,算是对洗牌这个过程的数学模型有一个比较全面的认识。这一篇中,我们就具体的Riffle shuffle,Hindu Shuffle的过程进行建模,进而分析他们到底要几次才能基本洗乱的问题,其中仍然包括一些近似策略。另外,在确定性洗牌中,对比较特殊的Faro Shuffle的一些特殊的性质,我们也作了一些介绍。
Riffle Shuffle的随机过程模型
1. 分叠过程:两叠张数服从一个Categorical分布,其分出来各张的概率正比于以n / 2为期望,某给定方差的正态分布的概率密度值,方差越小标明分得越均匀;
2. 交叉落牌选择:每次落牌仅能从左右两叠中选择一叠,这服从伯努利分布,其概率要正比于剩余叠的张数的幂函数;
3. 落牌张数:考虑到扑克的粘滞效应,每次落下的牌从哪一叠还取决于上一张落牌所在的叠,故两种建模策略:
A. 对和上一次落牌所在叠进行概率分数加权;
B. 直接考虑每次落下张数服从1 + 伯努利分布,n = 剩余张数 - 1,p使得其下落张数期望为常数;当牌数量不足或为1时候,特殊处理。
由此,得洗牌过程中的随机过程如下公式和图所示:
其中,N为整叠牌的张数,Di为每一次落牌后两叠牌的剩余张数;

A模型中:
Sigma为分牌均匀系数,越大表示在期望为均分的条件下,每次越分布均匀的程度(源于方差);
Arpha为均匀系数,越大表明洗牌人能够均分扑克并尽量两叠均匀下落的程度;
Beta为粘滞系数,越大表明洗牌人越会一次落下一叠很大的牌;
B模型中:
Sigma和Arpha同A模型,n为每次落牌在剩余张数足够时的期望张数,同起到粘滞系数的作用。
图1 Riffle Shuffle分叠位置分布图
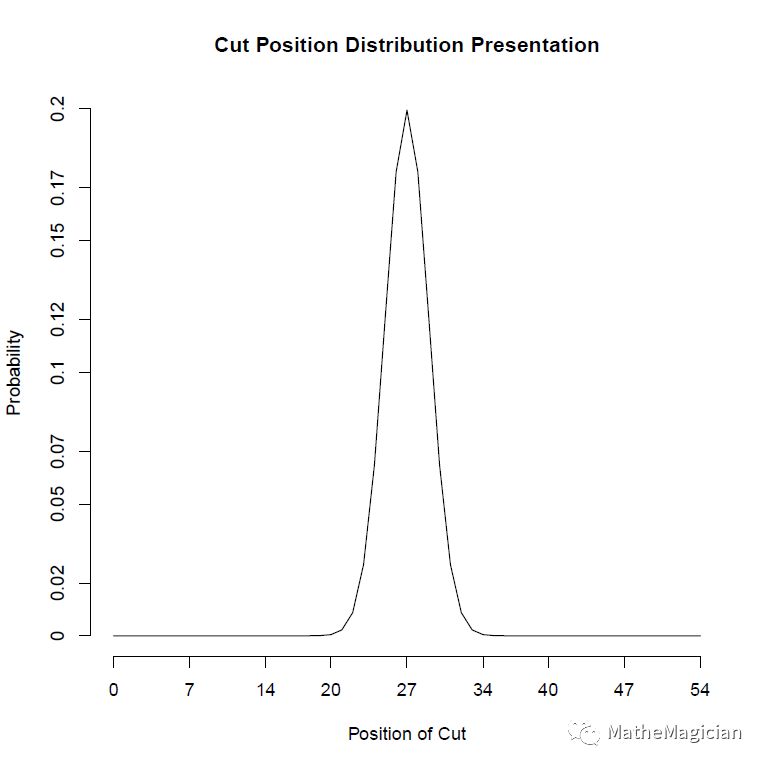
其实这些指标的不同取值已经可以判断一个人的洗牌水平,Sigma需要多次试验,而Arpha,Beta,n有一次洗牌就有足够的样本来估计了。
有趣的是,这种建模方法给不出一定洗出Perfect Shuffle的参数,因为那是另外一种技术了。
在完成这些思考的时候,也参考了一些前人的研究,最有名的是这个:Gilbert–Shannon–Reeds model。详情参考:
https://en.wikipedia.org/wiki/Gilbert%E2%80%93Shannon%E2%80%93Reeds_model
步骤和我的一样,但有几个区别:
1. 分叠过程我最开始也是用的二项分布,毕竟天然就是一个离散有限范围空间内的分布,但是无法同时保持期望为对半切开,空间给定,同时还能有可控的方差来表征一个人能否切均匀的能力,所以选用了正态分布离散化后的结果;
2. 落牌的伯努利分布参数正比于剩下张数的思路是很优秀的,我也借鉴,但是添加幂函数则有能表征其强度了;
3. 落牌其实有个很明显的点原文没有建模到是连续落牌,表明每次选择并非独立的,这里把历史条件考虑进来,或增加每次落牌张数因素构建粒度更粗的过程来描述,是更加贴合真实过程的。
站在巨人的肩膀上,一定可以看得更高,更远。
Hindu Shuffle的随机过程模型
每次以恒定参数的Poisson分布拿走顶部牌叠(假设每次抽的牌张数分布不随着剩余牌减少而变化),何时张数不够则全部拿走结束洗牌,这样的一族随机过程加上最后的Reverse操作即可模拟一次印度洗牌。
比如,给定poisson期望为5,加一得6张为一次期望的洗牌张数,即平均以9叠左右反序整个扑克牌(不是严格9叠,因为最后一叠往往不足量)。
公式描述如下:
其中,lamda为泊松系数,Reverse函数为序列翻转函数。
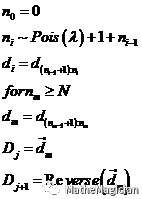
Faro Shuffle的函数过程模型
Faro Shuffle在我们的分类中属于非确定洗牌,本质上牌的熵增为0,所以可以看作并没有洗牌的效果。
其洗一次牌的过程是一个确定性过程,并且可以神奇的找到其恢复成原状的规律:
其中牌张数为偶数2N(否则无法均分进而无法完美洗牌),另外,ord函数在数学上叫做Multipicative Order,恰好即为所求。

对于没有大小王的一副扑克牌,N = 26,故out faro的恢复洗牌数量是8次,而in faro居然要52次之多,看起来这个数值随着牌的张数增加并没有什么规律,这看起来就是一个随机数发生器,而一副扑克牌在out faro下能够8次就完全恢复,不得不说这是一个奇迹搬的巧合。而加了大小王的out faro多了两张牌恰好和没有大小王的in faro结论相同,也要52次,失之毫厘,误差千里啊!
好了有了这些模型以后,我们就可以给出基于上一篇讲的用熵来度量不确定度的方案来具体估计到底洗多少次才能洗乱了,然而这件事情并不简单,在完成这个洗牌混乱评价的定义和过程建模以后,其真实的计算过程远比我们想的复杂。
研究了这么多洗牌方法和混乱度,这里我们放松一下,简单讨论一个前面提到的相关问题:
扑克游戏,一定要洗乱才公平吗?
其实,我们一般的扑克游戏的所谓公平,并不需要洗得完全混乱,只要对玩家和拿到的牌点是独立的,那这个游戏就是公平的。这一点,只需要起牌顺序是随机的就能够做到,至于牌没有洗乱其实是造成斗地主之类的两房差距悬殊而已,但并不是不公平,只是这是一个靠运气多过靠实力的游戏而已。然而依次摸牌过程又相当于一次系统抽样,其实真的没有洗也无所谓了,何况QQ斗地主上还有不洗牌玩法,通过不洗牌加批次抽样使得牌的点数分布差异更大(差异要根据游戏种类来,在斗地主游戏中其实是这副牌好打得程度,即平均胜率),但并不影响游戏的公平性。
那不洗乱的扑克牌到底对游戏有什么伤害呢?
其实这不影响公平,但影响玩家实力发挥的程度。
一个游戏是否依赖实力还是运气则是建立在公平条件下另一个更深的评价维度,可以定义为实力系数(正数)a,有
P(L1 win L2) = logistic(a(L1 - L2))
L1,2为对战双方的实力评分,取正数,其差的绝对值期望应该校正到相等才能相互比较a。a越大则表示实力强的一方完胜,弱的一方完全没有机会,实际上王者荣耀这类实时竞技游戏的玩家匹配大多用的这个方法来评价胜率的。
a如果很大,这一极端就是围棋了。完全信息博弈下,几乎没有任何随机扰动,每一盘棋几乎由你的水平决定而没有临时的运气成分,哪怕先手和后手的一点点的系统误差都在计算目数的时候校正了。
而a接近0的极端就是三公或者石头剪刀布了,他们虽然公平,但是并不存在什么实力的事。
适中的a比如斗地主,升级,德州扑克,麻将等,既有实力成分,又免不了一定运气成分。
需要那么一点点运气加实力的游戏由于双方获胜概率不会悬殊,往往会增加前面说的熵,那么理论上对人们的吸引程度更大(完全随机的又会因为不感兴趣而直接不关注,熵再大也没用),我想足球篮球风靡世界多半和这个有关吧,而围棋再精妙,不搞出个人工智能AlphaGo来,恐怕也难以受到大面积关注。
但是,赌场里面的猜大小,21点之类的游戏连公平都算不上,更靠不了实力了,实力顶多输的少一点而已。
最后,附上一个和今天介绍的完美洗牌相关的魔术,感谢朋友给我提供的点子,解析会在后面的文章中分享。
视频1 完美三明治
大好消息!为回馈MatheMagician的广大用户,本公众号正进行第二期“留言点赞送扑克”活动,详情请点击:当扑克牌遇上数学!查看活动详情,也可以直接扫描下方图片内的二维码直接购买。

好了,今天的数学魔术师的分享就到这里,希望各位客官能够喜欢!这里是MatheMagician,有你要的奇迹!
再次感谢各位客官的欣赏,MatheMagician期待您的赞赏哦~
更多精彩内容欢迎扫描下方二维码或点击头部公众号名MatheMagician关注我们,更欢迎把我们的精彩内容奔走相告,我们下期再见!

我们是谁:
MatheMagician,中文“数学魔术师”,是一个十分冷门的职业,原指用喜欢用数学原理设计魔术的魔术师或数学家。但由于数学太过艰深,变成魔术又表演困难,所以这个领域的专业研究者及其罕见。但其实,魔术设计只是数学建模的一个别致的场景;而魔术本身也蕴含着数学之外的诸如心理学,行为科学等其他广阔的议题。我们文章分享的内容涵盖统计,算法,NLP等前沿的数学及应用领域;也包括魔术思想,流程解析,鉴赏等关于魔术的思考;还有大量直接结合二者设计的数学魔术的分享。如果你对数学或者魔术感兴趣,或者喜欢思考和有内涵的文字,我们的内容一定能成为你学习成长的好伙伴!欢迎在文末或公众号留言与我交流!
往期精彩:
点击阅读原文,往期精彩不错过!




















 790
790

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








