1. 概述
这篇文章提出了一种“try-and-learn”的算法去训练pruning agent,并用它使用数据驱动的方式去移除CNN网络中多余的filters。借助新的奖励机制,agent可以大量移除CNN网络中的filters,并且保持网络的精度在期望的水平内。在网络性能和规模上提供了很好的操控性。
这篇文章中的方法具有如下特点:
1)使用数据驱动的方法去剪枝。并且通过实验数据驱动方法剪枝的效果是好于手工设置的剪枝条件(类似L1与L2范数);
2)文章的方法在网络的性能与规模上在剪枝期间提供了很好地操控性。当确定了网络的期望性能之后,本文的方法可以实现完全自动实现网络剪枝。
为了实现这样的目标,论文中将剪枝问题转化为了“try-and-learn”的学习任务。也就是训练一个pruning agent,使用神经网络建模,输入filter的权重输出该filter是否保留的二值标识。该agent是使用新的奖励机制(尽可能高的裁剪比例)来训练,同时保持网络性能保持在特定的水平上。
直观地把论文中的方法看作是一个“try-and-learn”的过程,最开始的时候从全部的filter中随机剪枝一个,每次进行剪枝操作会通过奖励机制评估。这个评估会返回给agent,这迫使agent去产生更高的回馈。但是这样的操作的可执行空间是很大的,对于有64个filter的层,可能性就有2642^{64}264,论文中给出了一种高效的算法来解决。
2. 网络剪裁
2.1 单层网络剪裁
这里对拥有LLL层卷积的CNN网络使用lll表示,用NlN_lNl表示第lthl^{th}lth层中filter的数量,filter的矩阵可以表示为Wl={w1l,w2l,…,wNll}W^l=\{w_1^l,w_2^l,\dots,w_{N_l}^l\}Wl={w1l,w2l,…,wNll},其中wil∈Rml∗h∗ww_i^l\in R^{m^l*h*w}wil∈Rml∗h∗w,需要训练的agent用πl\pi^lπl表示,它用WlW^lWl作为输入,产生操作的二值标识,Al={a1l,a2l,…,aNll}A^l=\{a_1^l,a_2^l,\dots,a_{N_l}^l\}Al={a1l,a2l,…,aNll},对于agentπl\pi^lπl使用参数θl\theta^lθl参数化,则就可以表示为πl(Al∣Wl,θl)\pi^l(A^l | W^l,\theta^l)πl(Al∣Wl,θl)。
对于这个训练任务给定验证集Xval={xval,yval}X_{val}=\{x_{val}, y_{val}\}Xval={xval,yval},优化的目标函数是L=R(Al,Xval)L=R(A^l, X_{val})L=R(Al,Xval),其中RRR是由两部分组成的,一个是accuracy term,另外一个是efficiency term。
R(Al,Xval)=ψ(Al,Xval,b,p∗)∗ϕ(Al)R(A^l, X_{val})=\psi(A^l,X_{val},b,p^*)*\phi(A^l)R(Al,Xval)=ψ(Al,Xval,b,p∗)∗ϕ(Al)
对于 accuracy term ,它保证在验证集上性能的下降在度量MMM下下降的边界是bbb,bbb这个参数是用来调控剪裁力度与网络性能的。参数p∗p^*p∗是原始网络fff的性能,p^\hat{p}p^是剪裁之后新网络fAl^\hat{f_{A^l}}fAl^的性能。当然在剪裁之后是需要经过训练集finetune再去测量剪裁之后网络的性能的。度量指标MMM在分类问题中就代表准确率,在分割问题中就代表全部的准确率。那么这部分就可以描述为如下的形式:
ψ(Al,Xval,b,p∗)=b−(p∗−p^)b\psi(A^l,X_{val},b,p^*)=\frac{b-(p^*-\hat{p})}{b}ψ(Al,Xval,b,p∗)=bb−(p∗−p^)
p^=M(f^Al,Xval),p∗=M(f,Xval)\hat{p}=M(\hat{f}_{A^l}, X_{val}), p^*=M(f, X_{val})p^=M(f^Al,Xval),p∗=M(f,Xval)
对于 efficiency term ,C(Al)C(A^l)C(Al)代表其中值为1(也就是被保留)的数量,然后其可以使用下面的算式进行度量:
ϕ(Al)=log(NlC(Al))\phi(A^l)=log(\frac{N^l}{C(A^l)})ϕ(Al)=log(C(Al)Nl)
之前提到agent中使用参数θ\thetaθ,那么整个的目标函数就可以使用梯度下降法进行求解,
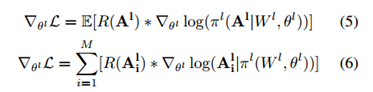
那么整个层的裁剪算法就可以被描述为:

2.2 多层网络裁剪
对于整个网络中的agent使用π={π1,π2,…,πL}\pi=\{ \pi^1,\pi^2,\dots,\pi^L\}π={π1,π2,…,πL}进行表示。其剪枝的策略还是逐层进行的,每剪完一层就进行finetune进行回血,之后再剪下一层,这样一层一层,剪裁比例从小到大得到的剪枝结果是好于一次性剪除所有layer中的filter的。

3. 论文实验
3.1 VGG网络
下图展示分别对各层进行裁剪得到的错误率与剪裁之后filter的前后对比,这里设置的精度边界b=2b=2b=2。
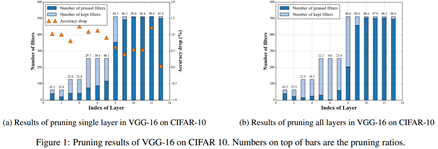
接下来调整裁剪的边界得到下图:
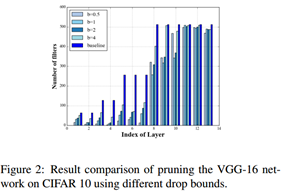
自然的裁剪的精度损失容忍度越大,裁掉的也就越多了。
3.2 ResNet网络
这篇论文中对ResNet的剪裁还是剪裁残差块中的第一个卷积,对于shortcut相连的部分并没有做处理。下图是使用不同精度损失容忍度对ResNet进行裁剪得到的结果
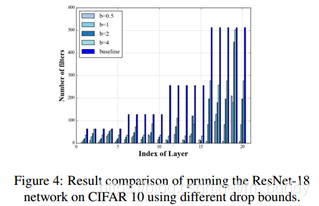
4. 个人总结
这篇论文使用参数化裁剪的形式,使用训练的形式来学习参数,使得裁剪在规定的精度误差范围内朝着裁剪比例尽可能大的方向迭代,从而得到最后的裁剪结果。但是,这篇论文中涉及到的方法并没有开源,直接复现难度比较大,存在风险,最好的还是提供代码,我们先去做复现验证,再决定运不运用到实际中去。





 提出一种try-and-learn算法,用于训练剪枝代理,以数据驱动方式移除CNN多余滤波器,保持网络精度的同时大幅减少网络规模。
提出一种try-and-learn算法,用于训练剪枝代理,以数据驱动方式移除CNN多余滤波器,保持网络精度的同时大幅减少网络规模。



























