1. 概述
使用SFM或者SLAM方法时,其前提假设是所处场景为静态的,也就是其中没有运动的物体。但这样的条件其实在实际中很多时候是不成立的,如道路场景,对此需要一种方法将场景中运动的目标从场景中区分出来。通常情况下会使用如语义分割或是实例分割的形式,抽取场景中固定目标的掩膜,之后从SFM方法中排除出去,从而避免这些运动目标给位姿估计和场景重建带来影响。但是这样的方法存在无法区分真实运动目标的能力,也就是对于属于具备行动能力,如车、人,也会存在静止的情况,一股脑直接从算法中排除出去也不具有合理性。而且语义分割和实例分割需要预先假定可移动目标的类别,不在这些类别中的运动物体是无法被探测到的。
对此,经过一些调研发现无监督视频目标分割(Unsupervised video object segmentation)与所期望的需求由一定关联性,在该类型方法也需要去分析视频数据中的主要运动目标,之后使用mask的形式进行描述,这与期望的效果一致。不过上述无监督视频目标分割在训练的过程中也并不是完全无监督的形式,也需要认为去确定需要分割的mask,这一点上与显著性目标分割有点类似,而运动信息(光流)就显得不是那么至关重要了。不过不管怎么说该类型方法也算是为解决运动目标问题提供一些思考。
此时(03.18.2023)暂就对无监督视频目标分割的一些方法研究,后续对场景中运动目标处理的方法或思路也将在这里进行更新。
03.20.2023更新:
对于运动的物体其属性是不满足相机位姿约束的,也就是在给定的深度值和位姿,经过warp变换之后运动目标的mask与真实图像运动目标的mask是存在一定偏差的,则依据这个特性可从预先定义好的实例mask中区分出实际发生了运动的目标,进而将其排除。
2. 无监督视频目标分割
benchmark:Paper With Code:unsupervised-video-object-segmentation
2.1 MATNet
paper:Motion-Attentive Transition for Zero-Shot Video Object Segmentation
code:MATNet
该方法是motion-appearance的,输入的数据是RGB图像和光流估计,它们分别输入各自编码器抽取特征,使用MAT和SSA模块实现两种类型数据的融合,融合之后的多尺度特征通过BAR模块实现多尺度mask预测。
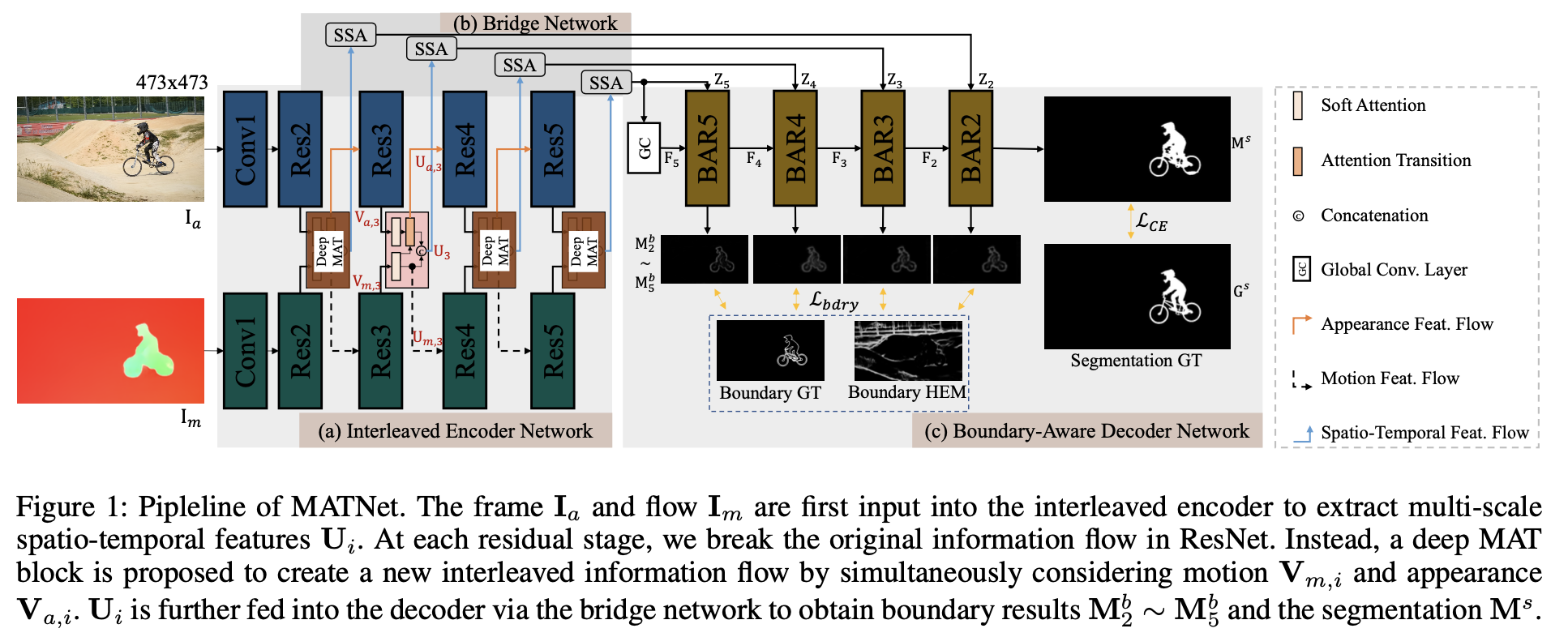
MAT模块:
使用光流和RGB图像的特征做coss-attention操作,其运算步骤如下图所示:
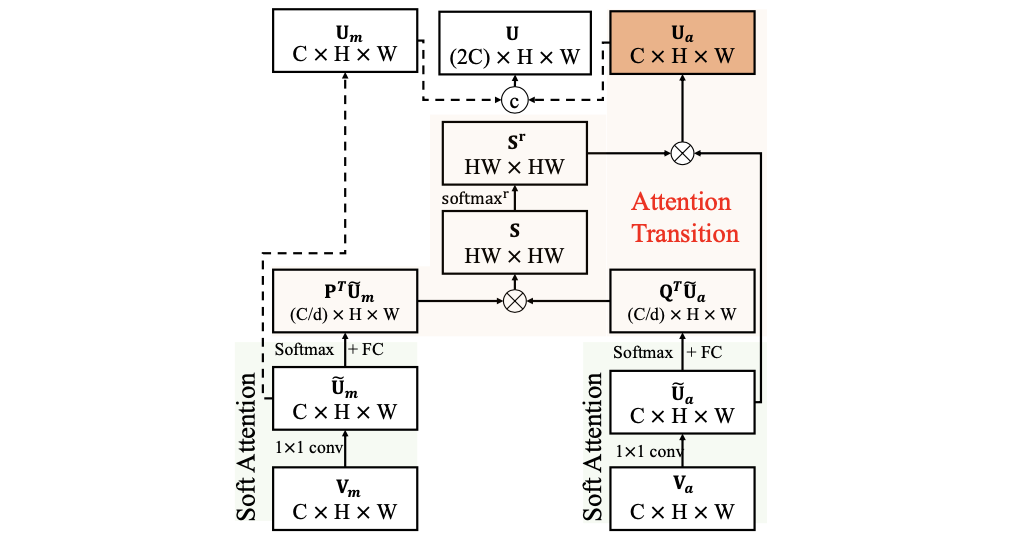
SSA模块:
该模块是通过CABM(channel&spatial上的attention)和一个可学习的scale参数共同构成,用于得到编码器部分最后的特征。
BAR模块:
该模块是用于最后目标mask分割,在其中添加了ASPP和boundary预测用于优化最后分割结果,其结构见下图所示:
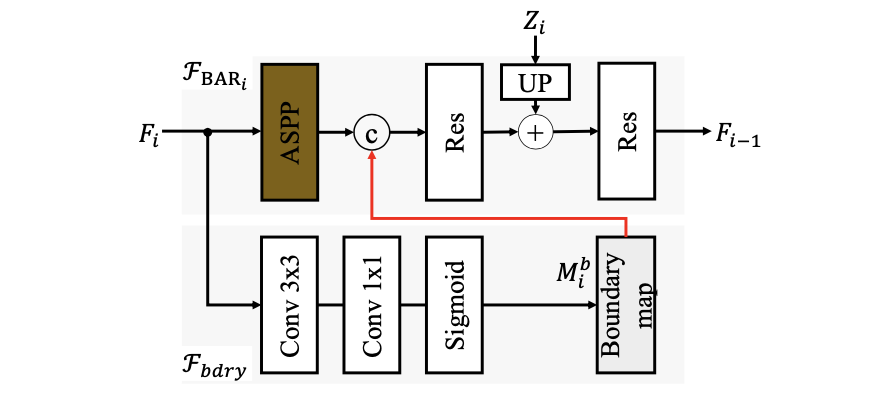
性能比较:
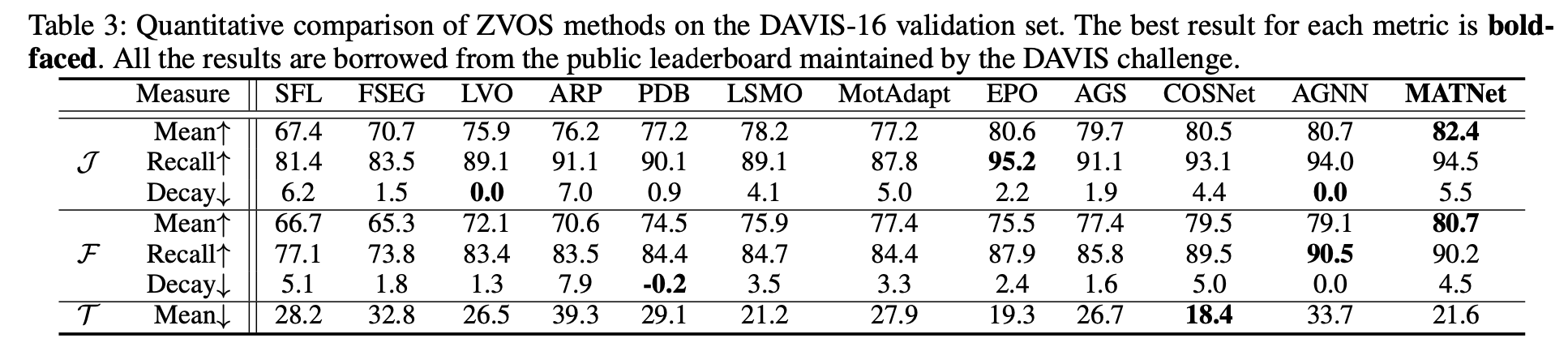
2.2 AMCNet
paper:Learning Motion-Appearance Co-Attention for Zero-Shot Video Object Segmentation
code:AMC-Net
这篇文章提出的方法结构与上一篇文章的结构相似,也是在motion和appearance之间建立关联性,之后通过多尺度预测得到最后结果,其网络结构见下图所示:
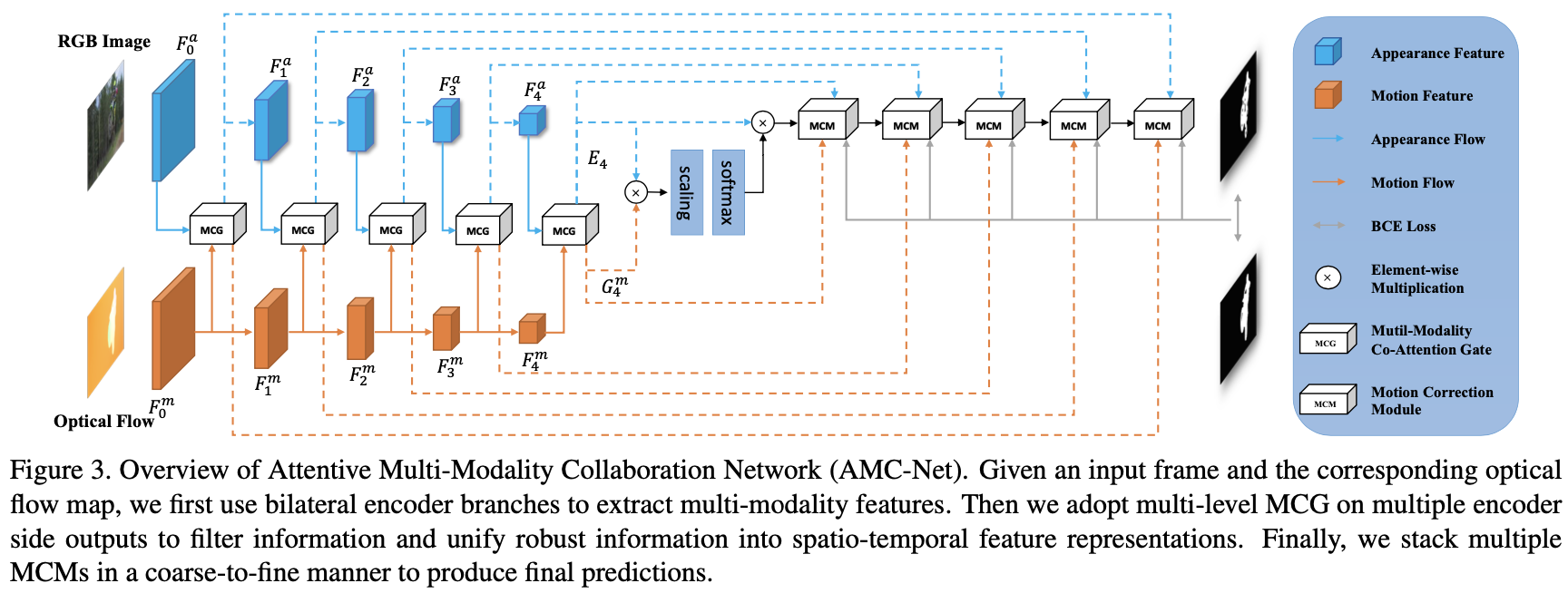
与前面的方法不同的是motion-appearance特征聚合方法以及最后解码单元存在差异,这两者的结构如下图:
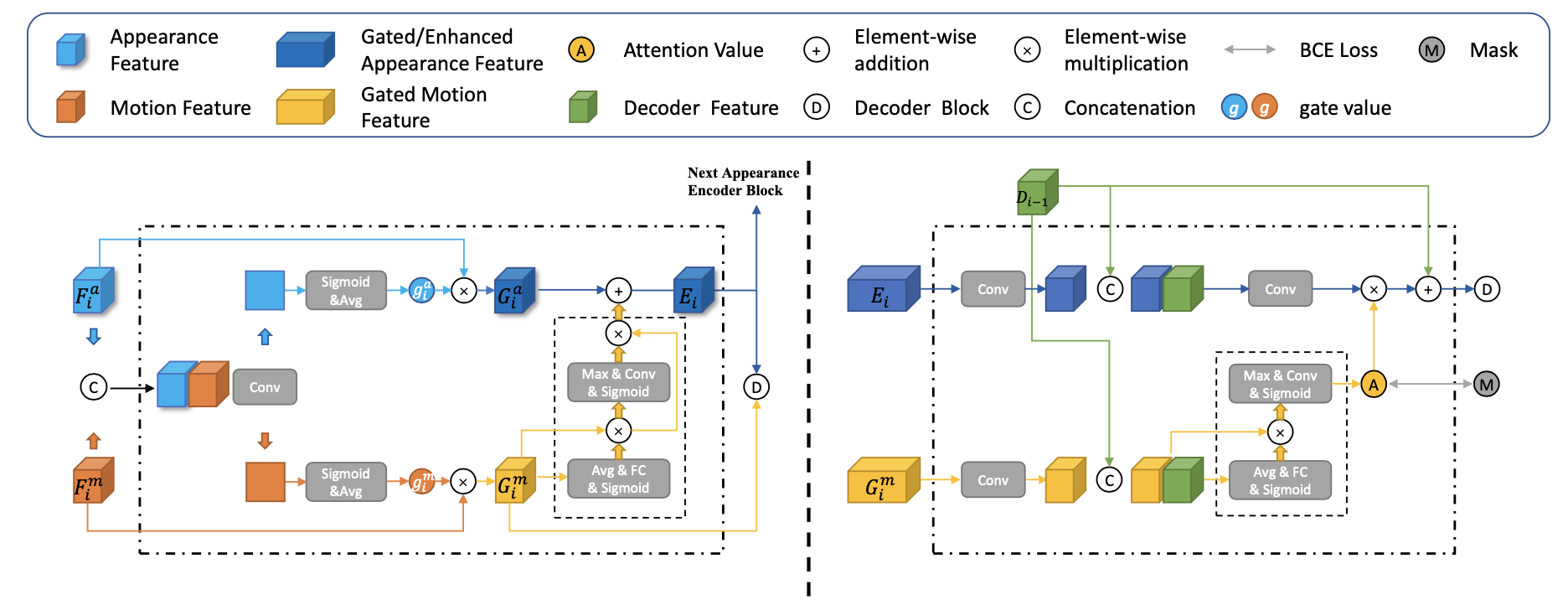
性能比较:
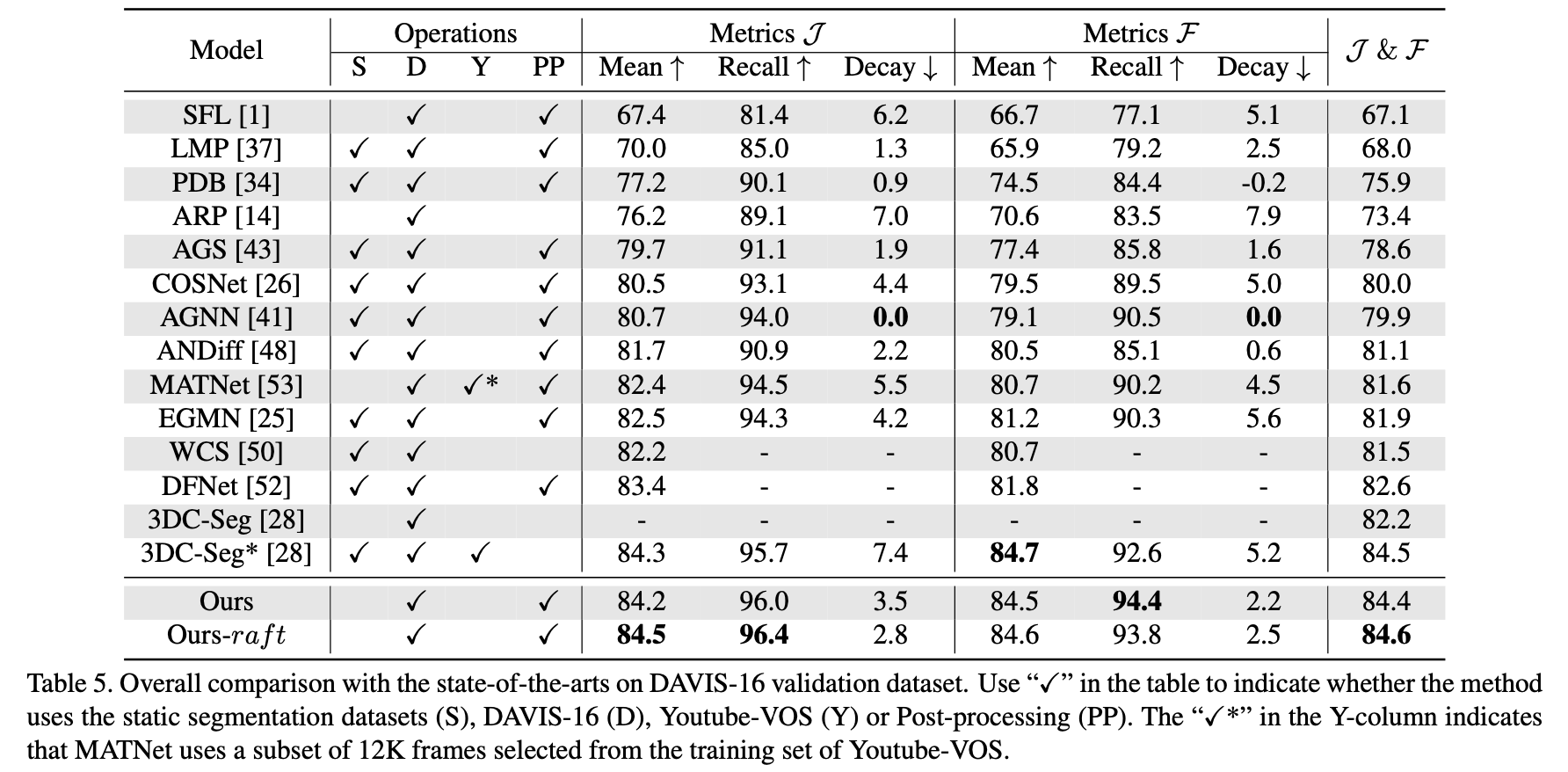
2.3 TMO
paper:Treating Motion as Option to Reduce Motion Dependency in Unsupervised Video Object Segmentation
code:TMO
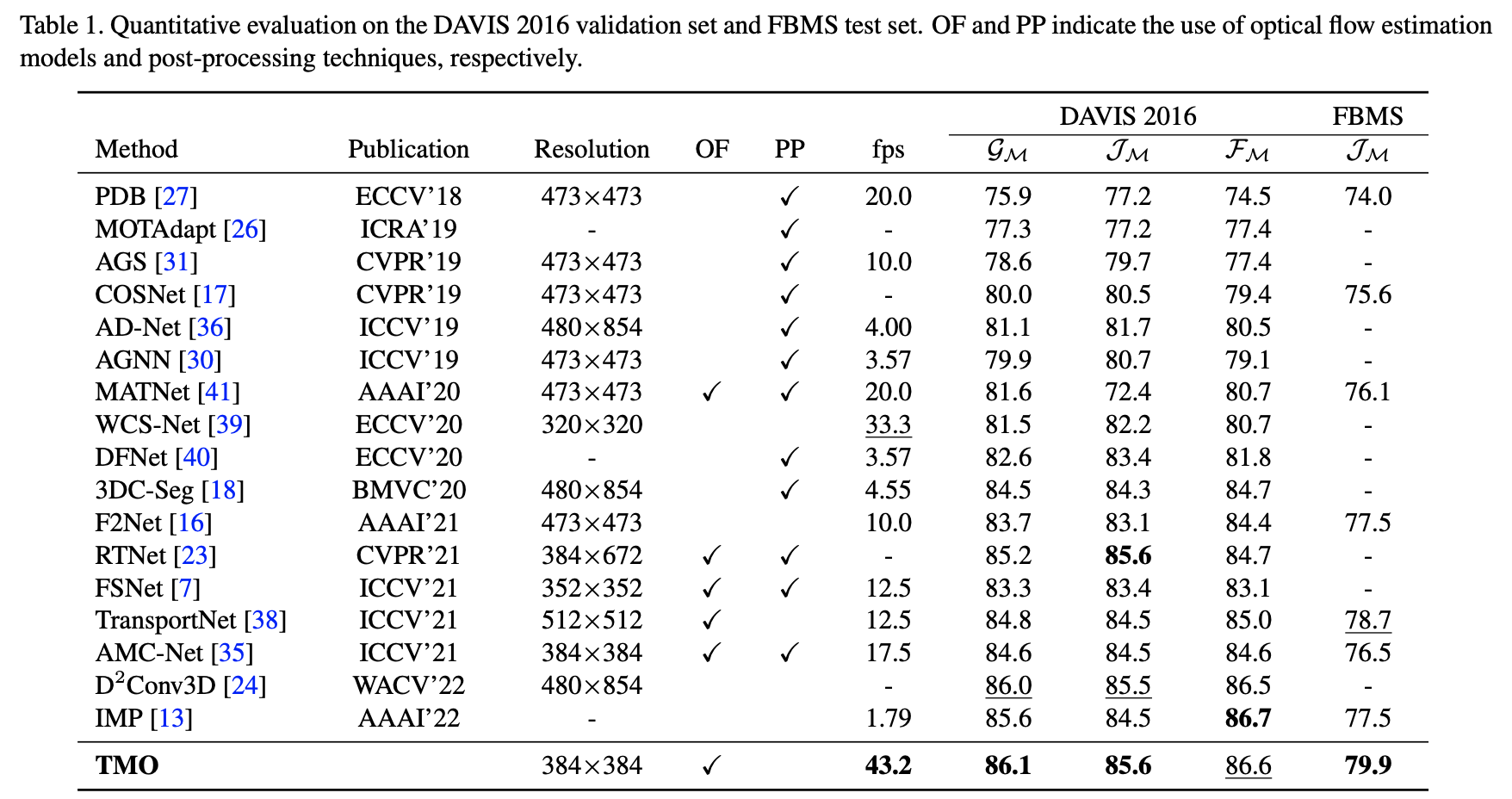
在之前的方法中都显式使用光流估计结果,其采用的光流估计网络为PWCNet或者是CRAFT,但光流在实际使用过程中光流的质量却是参差不齐的,太过于依赖光流估计的结果显然是存在一定问题的,对此这篇文章的方法去掉了前面两种方法中关于motion-appearance做corr-attention的步骤,而是直接通过在解码器中对GT所需要的特征进行自适应选择,其网络结构见下图所示:
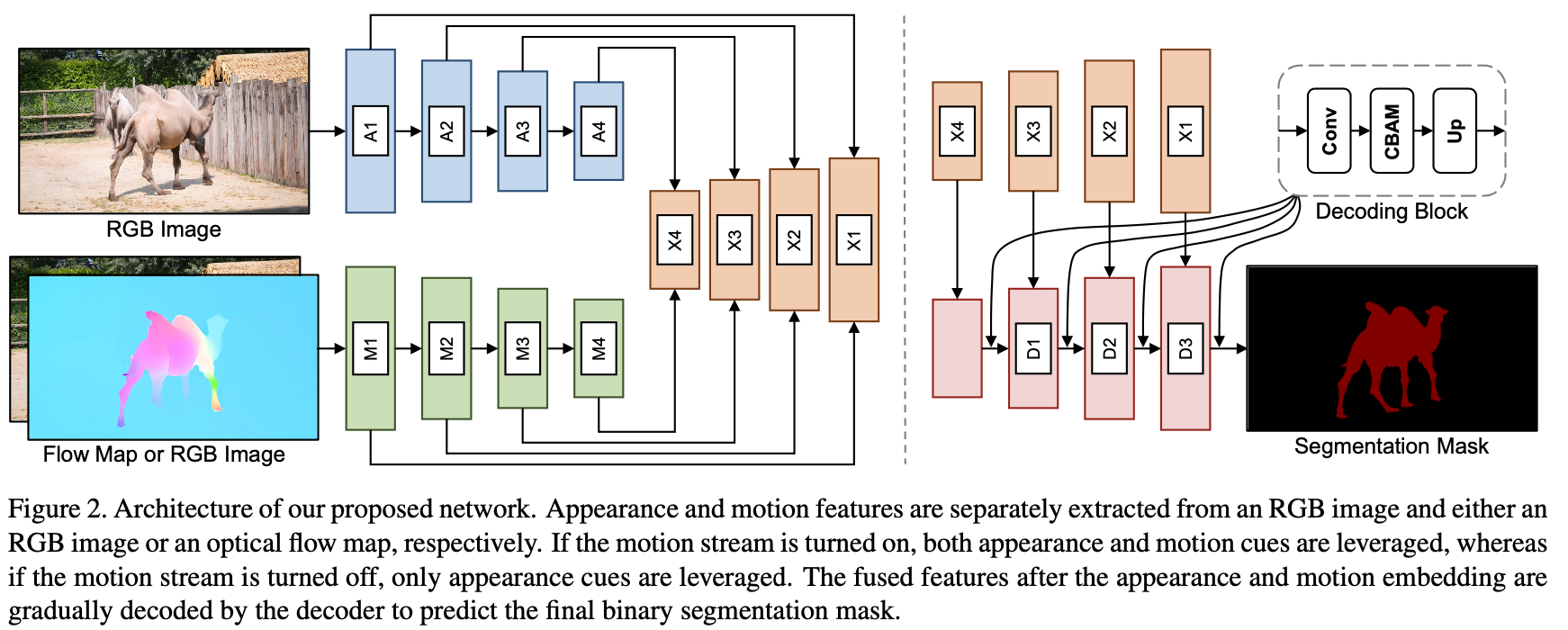
性能对比:
3. 基于深度和位姿warp校验
3.1 Dyna-DM
paper:Dyna-DM: Dynamic Object-aware Self-supervised Monocular Depth Maps
code:Dyna-DM
在自监督深度估计算法中运动目标会给位姿估计网络带来影响,进而会影响深度估计的质量,则采用实例分割将具备运动属性的目标从图像中移除便是解决方案之一,但是存在无法区分真实运动目标的能力,如下图:

对此,文章首先将图像中所有具备运动可行性的目标都检测出来,使用去除这些区域的图像进行相对位姿估计和深度估计。接下来便是需要设计逻辑排除场景中真实的运动目标,首先使用阈值排除那些占据图像比较小的区域(阈值为全图像素的0.75%),之后使用构建出的位姿和深度结果对疑似运动目标的mask进行warp,比较warp之后前后帧mask之间的重贴程度(文中用dice系数作为评判标准,阈值取0.9),其流程见下图所示:
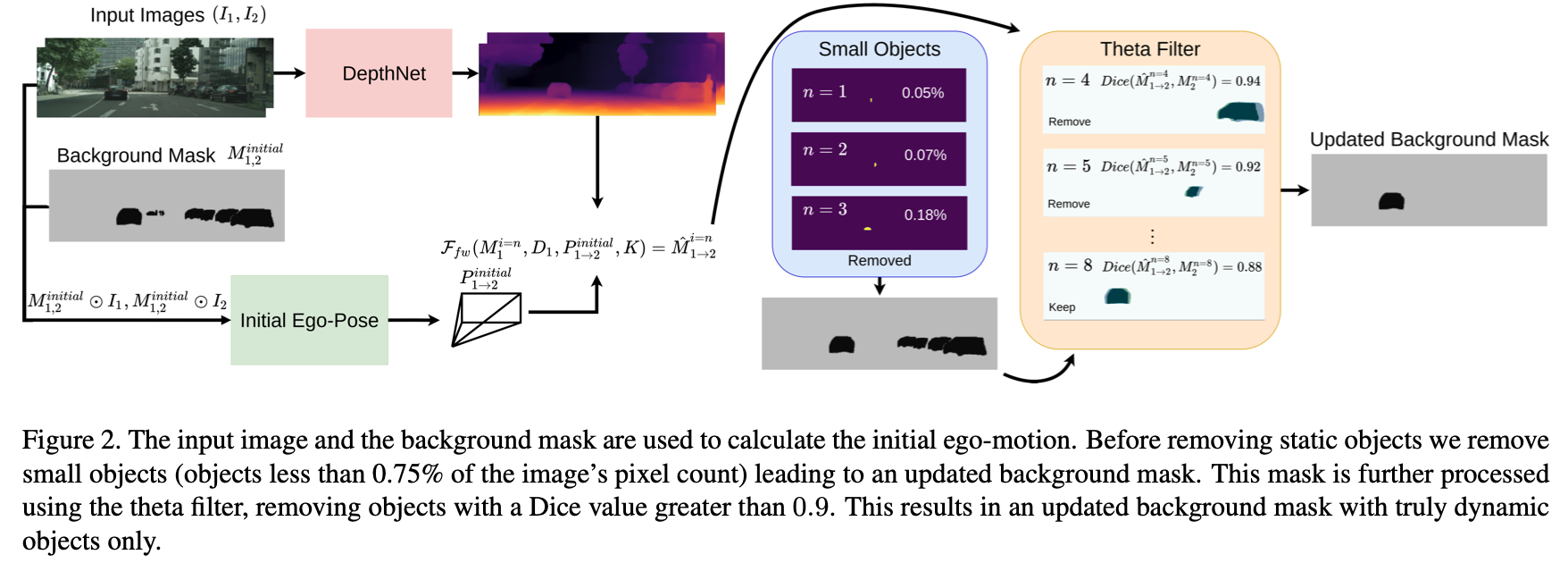
按照上图中的假设,运动的目标其前后帧mask经过warp之后应该重叠区域较小,也就是dice系数偏低,其实际的测试表现也是如此,看如下动静目标在该指标下的比较:
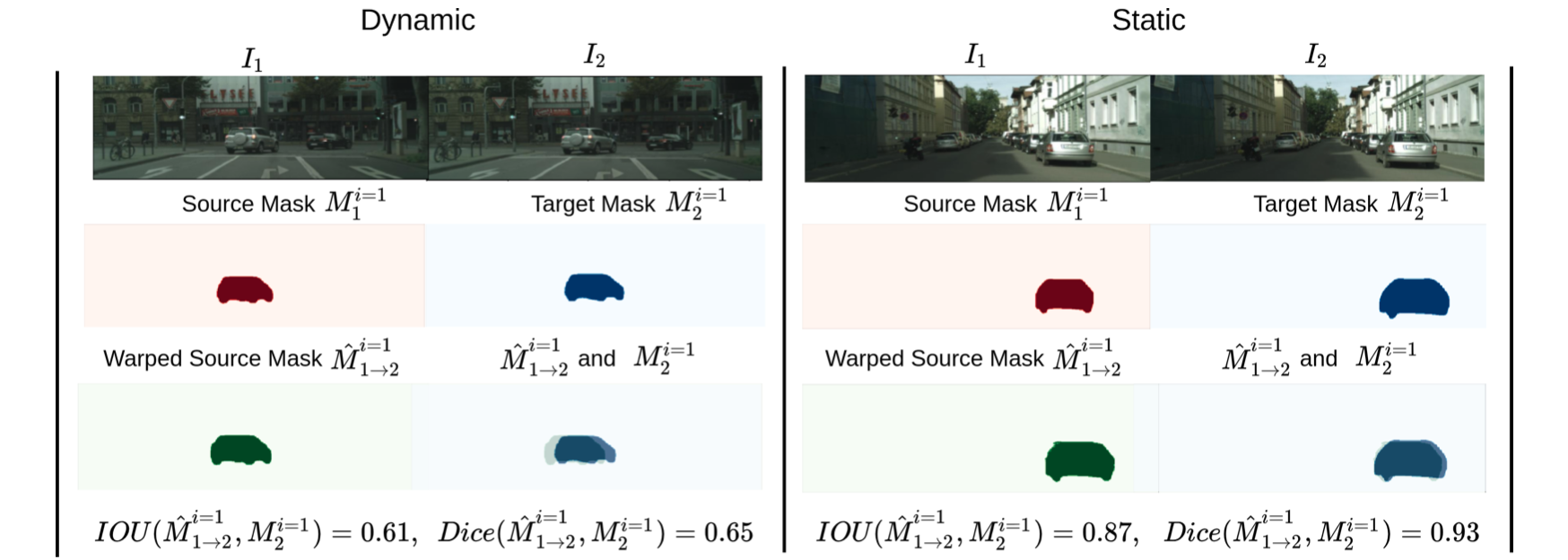
性能比较:

 动态场景中运动目标处理与位姿建图鲁棒性研究
动态场景中运动目标处理与位姿建图鲁棒性研究





 本文探讨了在使用SFM或SLAM时,如何处理动态场景中的运动目标,以提高位姿估计和场景重建的准确性。重点介绍了无监督视频目标分割方法MATNet、AMCNet和TMO,并提出基于深度和位姿warp校验的Dyna-DM算法,用于动态对象感知的自我监督单目深度映射,增强了算法的鲁棒性。
本文探讨了在使用SFM或SLAM时,如何处理动态场景中的运动目标,以提高位姿估计和场景重建的准确性。重点介绍了无监督视频目标分割方法MATNet、AMCNet和TMO,并提出基于深度和位姿warp校验的Dyna-DM算法,用于动态对象感知的自我监督单目深度映射,增强了算法的鲁棒性。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








