《Unsupervised Monocular Depth Learning in Dynamic Scenes》论文笔记

参考代码：depth_and_motion_learning

1. 概述

导读：这篇文章是在（Depth from Videos in the Wild）的基础上进行改进得到的，在之前的文章中运动区域/物体通过mask标注或是bounding box标注的形式确定，但是这样或多或少会存在对外依赖的问题。对此，文章从 刚性物体运动 在相机前运动的特性进行分析得出如下两个特性：
1）其在整幅图像中的占比是较少的，毕竟一般情况下不会运动的背景占据了较大的比例；
2）刚性运动的物体其内部运动特性是分段的常量值，也就是对应的梯度变化很小；
正是基于上述两点观察，文章在之前文章的基础上对运动物体区域构建了一个约束，从而减少了运动物体会深度估计带来的影响。

文章的方式是通过隐式约束的形式对刚性物体运动区域进行约束，从而避免了显示地对运动区域标注，因而文章的方法可以在输入2帧图像的情况下实现深度预测和物体运动感知，如下图所示：

2. 方法设计

2.1 网络结构

文章的网络结构如下图所示：

整体上这里网络结构与之前文章（Depth from Videos in the Wild）的网络结构类似，只是在一些细节上有所区别。这里深度估计网络的编解码结构是一致的，主要的不同点在相机位姿和内参估计网络上，在原本两帧图像输入基础上添加了深度估计结果作为输入。

2.2 损失函数

深度图平滑损失：
这部分损失是为了给深度估计结果带来平滑作用，减少噪声的产生，其损失函数描述为：
$$L_{reg,dep}={\alpha }_{dep}\iint (|{\partial }_{u}d(u,v)e^{-{\partial }_{u}I(u,v)}+{\partial }_{v}d(u,v)e^{-{\partial }_{v}I(u,v)}|d_u{d}_v$$

循环一致性损失：
首先是变换矩阵的循环一致性约束，其描述为：
$$L_{cyc}={\alpha }_{cyc}\frac{||R{R}_{inv}-1|{|}^2}{||R-1|{|}^2+||R_{inv}-1|{|}^2}+{\beta }_{cyc}\iint \frac{||R_{inv}T(u,v)+T_{inv}(u_{warp},v_{warp})|{|}^2}{||T(u,v)|{|}^2+||T_{inv}(u_{warp},v_{warp})|{|}^2}{d}_u{d}_v$$
图像域的循环一致性约束，描述为：
$$L_{rgb}={\alpha }_{rgb}\iint |I(u,v)-I_{warp}(u,v)|1_{D_{u,v}>D_{warp}(u,v)}{d}_u{d}_v+{\beta }_{rgb}\frac{1-\mathcal{S}\mathcal{S}\mathcal{I}\mathcal{M}(\mathcal{I},{\mathcal{I}}_{warp})}{2}$$

物体移动约束损失：
这部分损失主要是完成下面的两个作用：

• 1）根据上文提到的稀疏特性，对运动场做稀疏化约束，这里使用的$L\frac{1}{2}$，文章指出该函数具有更好的稀疏特性；
• 2）基于刚性物体运动的分析，对刚性物体运动场施加梯度损失，使其在分布呈现分段的常量值特性；

首先对于常量值特性，添加梯度约束：
L g 1 [ T ( u , v ) ] = ∑ i ∈ { x , y , z } ∬ ( ∂ u T i ( u , v ) ) 2 + ( ∂ v T i ( u , v ) ) 2 d u d v L_{g1}[T(u,v)]=\sum_{i\in \{x,y,z\}}\iint \sqrt{(\partial_uT_i(u,v))^2+(\partial_vT_i(u,v))^2}d_ud_v Lg1​[T(u,v)]=i∈{x,y,z}∑​∬(∂u​Ti​(u,v))2+(∂v​Ti​(u,v))2 ​du​dv​

接下来对稀疏化添加约束：
L 1 2 [ T ( u , v ) ] = 2 ∑ i ∈ { x , y , z } ⟨ ∣ T i ∣ ⟩ ∬ ( 1 + ∣ T i ( u , v ) ∣ ⟨ ∣ T i ∣ ⟩ d u d v L_{\frac{1}{2}}[T(u,v)]=2\sum_{i\in \{x,y,z\}}\langle|T_i|\rangle\iint \sqrt{(1+\frac{|T_i(u,v)|}{\langle|T_i|\rangle}}d_ud_v L21​​[T(u,v)]=2i∈{x,y,z}∑​⟨∣Ti​∣⟩∬(1+⟨∣Ti​∣⟩∣Ti​(u,v)∣​ ​du​dv​

则这部分整体的损失函数描述为：
$$L_{reg,mot}{\alpha }_{mot}{L}_{g1}[T_{obj}(u,v)]+{\beta }_{mot}{L}_{\frac{1}{2}}[T_{obj}(u,v)]$$
则对应的损失函数实现可以参考：

# losses/loss_aggregator.py#L283
normalized_trans = regularizers.normalize_motion_map(
    residual_translation, translation)
self._losses['motion_smoothing'] += scale_w * regularizers.l1smoothness(  # 对应公式2，分段常量值约束
    normalized_trans, self._weights.motion_drift == 0)
self._losses['motion_drift'] += scale_w * regularizers.sqrt_sparsity(  # 对应公式3，稀疏性约束
    normalized_trans)

上面提到的几点约束的消融实验结果：

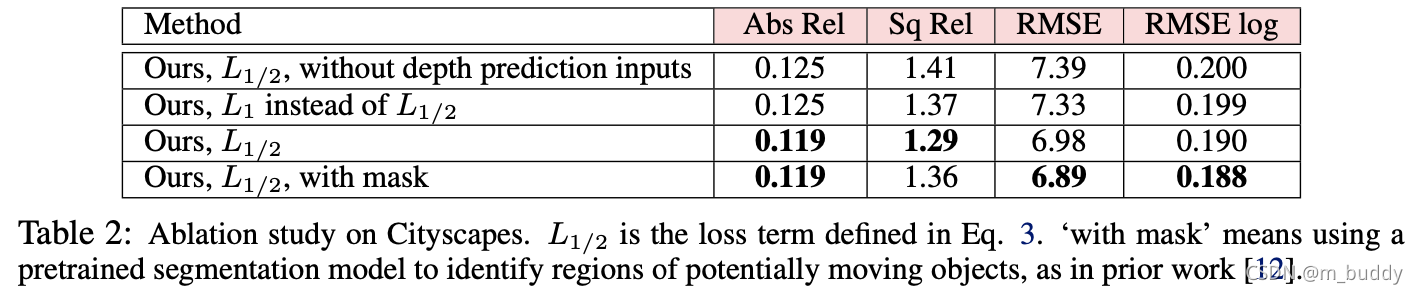
3. 实验结果

Cityscapes数据集上性能对比：

KITTI数据集上性能对比：