代码地址:
1. 概述
导读:卷积网络的剪裁对于模型部署到终端机上具有很强的实际意义,但是现有的一些剪裁算法存在训练并不高效,人工设计剪裁方案耗时费力,其原因就是缺少对于网络中非重要成分的指引。这篇文章中在特征图中搜寻具有High Rank(HRank)特性的filter(参考矩阵分解的内容),之后将那些具有low-rank对应的filter剪除掉,从而达到网络瘦身的目的。文章的方法的原理是:由一个filter产生的特征图他们的rank均值是是一致的,CNN网络中batch参数对其无影响,文中使用数学证明的形式表明那些具有low-rank属性的filter具有较少的信息,而那些hight-rank属性的filter具有更加丰富的信息。基于这样的思路文章的方法在ResNet-110上实现了58.2%的FLOPs减少,精度损失0.14%(CIFAR-10数据集top-1),ResNet-50减少43.8%的FLOPs,精度损失1.17%(ImageNet数据集top-1)
一般来讲对于网络的剪裁分为种类型:weight pruning(非结构化剪枝)和filter pruning(结构化剪枝)。由于第一种剪枝策略产生的是稀疏的权重矩阵,因而限制了一些主流矩阵运算库和硬件的使用,因而需要对其单独设计。而第二种剪枝方式则是对现有的硬件和运算库比较优化,也是现有的比较常用的一种剪枝压缩方法。对于这种剪枝压缩方法核心就是对于非重要filter的判断上,对此文章将其对于filter重要性的度量划分为两个类型:
- 1)Property Importance:这种类型的方法是建立在网络的固有属性上的,并不需要修改网络的损失训练损失函数,在完成剪枝之后需要finetune用以恢复精度。一些典型的方法有L1或L2范数/一阶梯度度量/特征图反向映射filter重要性/网络层的几何中值。这些方法会存在精度和压缩比例的局限;
- 2)Adaptive Importance:这种类型的方法是将剪裁的方法嵌入到网络的训练过程(给损失函数添加额外的正则项并使其稀疏)中,这样通过在网络训练过程中通过数据流的形式选择更加的裁剪方案。一些方法有:在BN中scaling稀疏/引入结构稀疏参数。这些直接在网络中加入的稀疏约束的方式一般比第一种方法中获得结果要好,但是由于网络的损失函数已经被改变,这就使得整个网络都需要重新训练而不仅仅是重新fintune了;
而这篇文章的方法是属于上面说到的第一种剪裁方法的,文章使用rank的属性对特征图进行筛选,从而将对应的filter剪除掉,其流程见下图所示:

此外,文章还发现网络的特征图rank均值其并不会根据训练batch的变化而变化(也就是对输入数据分布不敏感),见下图所示:

这就使得文章的算法可以在小批量的数据集上进行,从而不需要将整个数据集载入,因而效率就很高了。
2. 方法设计
2.1 变量定义
这里假设CNN网络拥有 K K K层卷积网络, C i C^i Ci代表第 i i i个卷积层,则该层的卷积参数可以表示为 W C i = { w 1 i , w 2 i , … , w n i i } ∈ R n i ∗ n i − 1 ∗ k i ∗ k i W_{C^i}=\{w_1^i,w_2^i,\dots,w_{n_i}^i\}\in R^{n_i*n_{i-1}*k_i*k_i} WCi={w1i,w2i,…,wnii}∈Rni∗ni−1∗ki∗ki,每个filter的参数维度为 w j i ∈ R n i − 1 ∗ k i ∗ k i w_j^i\in R^{n_{i-1}*k_i*k_i} wji∈Rni−1∗ki∗ki。则前一层的特征经过卷积之后生成的特征图表示为 O i = { o i i , o 2 i , … , o n i i } ∈ R n i ∗ g ∗ h i ∗ w i O^i=\{o_i^i,o_2^i,\dots,o_{n_i}^i\}\in R^{n_i*g*h_i*w_i} Oi={oii,o2i,…,onii}∈Rni∗g∗hi∗wi,这里对生成特征的batch和C维度进行了调换,用于后面数据驱动的filter权值选择。则经过选择之后可以分为两个子集: I C i = { w I 1 i i , w I 2 i i , … , w I n i 1 i } I_{C^i}=\{w_{I_1^i}^i,w_{I_2^i}^i,\dots,w_{I_{n_{i1}}^i}\} ICi={wI1ii,wI2ii,…,wIni1i}和 μ C i = { w μ 1 i i , w μ 2 i i , … , w μ n i 2 i } \mu_{C^i}=\{w_{\mu_1^i}^i,w_{\mu_2^i}^i,\dots,w_{\mu_{n_{i2}}^i}\} μCi={wμ1ii,wμ2ii,…,wμni2i}(代表重要的filter和非重要的filter),这两个子集是原filter集合的子集,它们两个合并之后就是原来的filter集合。
2.2 HRank计算流程
那么怎么去求解原有filter集合中的非重要的集合呢?论文中首先对其建立数学最优化模型:
min
δ
i
,
j
∑
i
=
1
K
∑
j
=
1
n
i
δ
i
,
j
L
(
w
j
i
)
\min_{\delta_{i,j}}\sum_{i=1}^K\sum_{j=1}^{n_i}\delta_{i,j}L(w_j^i)
δi,jmini=1∑Kj=1∑niδi,jL(wji)
s
.
t
.
∑
j
=
1
n
i
δ
i
,
j
=
n
i
2
s.t. \sum_{j=1}^{n_i}\delta_{i,j}=n_{i2}
s.t.j=1∑niδi,j=ni2
其中,
δ
∈
{
0
,
1
}
\delta \in \{0,1\}
δ∈{0,1},当当前的filter为非重要的filter的时候取值为1,
L
(
⋅
)
L(\cdot)
L(⋅)表示的是filter的重要性度量。
之前的很多论文就是在这个重要性度量上有所不同,而这篇文章中设计的度量函数希望的是度量对于输入图像(特征图)的分布与输出鲁棒,否则就会导致和之前一些方法一样取得次优解。这篇文章中将度量的对象放在了特征图上,而不是filter的权值,这样做的好处是可以很好共同反应filter与输入图像(特征图)的特性。因而上面建立的最优化模型就可以描述为:
min
δ
i
,
j
∑
i
=
1
K
∑
j
=
1
n
i
δ
i
,
j
E
I
−
P
(
I
)
[
L
^
(
o
j
i
(
I
,
:
,
:
)
)
]
\min_{\delta_{i,j}}\sum_{i=1}^K\sum_{j=1}^{n_i}\delta_{i,j}E_{I-P(I)}[\hat{L}(o_j^i(I,:,:))]
δi,jmini=1∑Kj=1∑niδi,jEI−P(I)[L^(oji(I,:,:))]
s
.
t
.
∑
j
=
1
n
i
δ
i
,
j
=
n
i
2
s.t. \sum_{j=1}^{n_i}\delta_{i,j}=n_{i2}
s.t.j=1∑niδi,j=ni2
其中,
I
I
I是输入的图像(特征图),其采样的分布是
P
(
I
)
P(I)
P(I),
L
^
\hat{L}
L^代表特征图切片
o
j
i
(
I
,
:
,
:
)
o_j^i(I,:,:)
oji(I,:,:)中信息的估计,因而
L
^
\hat{L}
L^和
L
L
L是呈现正相关的关系的,包含的信息越多自然当前的filter也就更加重要了,反之亦然。
因而当前的问题就已经转化为了去估计某个filter产生的特征的信息的度量函数
L
^
\hat{L}
L^,之前的一些度量方法对于输入的分布
P
(
I
)
P(I)
P(I)是很敏感,因而就需要找到一种对与输入分布不敏感的度量方式。因而文章就提出了使用rank概念的度量方式,因而特征图的度量就可以描述为:
L
^
(
o
j
i
(
I
,
:
,
:
)
)
=
R
a
n
k
(
o
j
i
(
I
,
:
,
:
)
)
\hat{L}(o_j^i(I,:,:))=Rank(o_j^i(I,:,:))
L^(oji(I,:,:))=Rank(oji(I,:,:))
其中,
R
a
n
k
(
⋅
)
Rank(\cdot)
Rank(⋅)是输入图像
I
I
I的rank,在输入图像对应的矩阵上使用SVD分解,并划分重要区域与非重要区域,得到:
o
j
i
(
I
,
:
,
:
)
=
∑
i
=
1
r
σ
i
μ
i
v
i
T
=
∑
i
=
1
r
‘
σ
i
μ
i
v
i
T
+
∑
i
=
r
‘
+
1
r
σ
i
μ
i
v
i
T
o_j^i(I,:,:)=\sum_{i=1}^r\sigma_i\mu_iv_i^T=\sum_{i=1}^{r^{‘}}\sigma_i\mu_iv_i^T+\sum_{i=r^{‘}+1}^r\sigma_i\mu_iv_i^T
oji(I,:,:)=i=1∑rσiμiviT=i=1∑r‘σiμiviT+i=r‘+1∑rσiμiviT
因而,文章将当前特征图包含的信息量描述为:
r
=
R
a
n
k
(
o
j
i
(
I
,
:
,
:
)
)
r=Rank(o_j^i(I,:,:))
r=Rank(oji(I,:,:))
2.3 网络的剪裁过程
在之前将网络的第
i
i
i层的特征
O
i
∈
R
n
i
∗
g
∗
h
i
∗
w
i
O^i\in R^{n_i*g*h_i*w_i}
Oi∈Rni∗g∗hi∗wi(这是经过维度变换之后的),那么对于每个filter生成的特征图表示为
o
j
i
∈
R
g
∗
h
i
∗
w
i
o_j^i\in R^{g*h_i*w_i}
oji∈Rg∗hi∗wi,这里的第一个维度代表的是输入的图像或是前一层的特征,也就是传统上的batch维度,因而这就使得这个特征天然与输入数据的分布存在密切的关联,这就对数据相当敏感了。但是所幸的是文章发现由某个filter生成的特征其rank不与输入的数据强相关(不同输入样本可以通过通过求取期望的形式进行平滑近似),而且其rank还可以表示数据含有信息的多少(冗余程度),有了这两个性质就可以对网络中不重要的成分进行剪裁了,因而度量网络层中的重要性就可以描述为(求取在某个filter下的rank期望):
E
I
−
P
(
I
)
[
L
^
(
o
j
i
(
I
,
:
,
:
)
)
]
≈
∑
t
=
1
g
R
a
n
k
(
o
j
i
(
t
,
:
,
:
)
)
E_{I-P(I)}[\hat{L}(o_j^i(I,:,:))]\approx \sum_{t=1}^gRank(o_j^i(t,:,:))
EI−P(I)[L^(oji(I,:,:))]≈t=1∑gRank(oji(t,:,:))
在实际的中文章将
g
=
500
g=500
g=500,因而可以将原来的最优化表达式描述为:
min
δ
i
j
∑
i
=
1
K
∑
j
=
1
n
i
δ
i
j
(
w
j
i
)
∑
t
=
1
g
R
a
n
k
(
o
j
i
(
t
,
:
,
:
)
)
\min_{\delta_{ij}}\sum_{i=1}^K\sum_{j=1}^{n_i}\delta_{ij}(w_j^i)\sum_{t=1}^gRank(o_j^i(t,:,:))
δijmini=1∑Kj=1∑niδij(wji)t=1∑gRank(oji(t,:,:))
s
.
t
.
∑
j
=
1
n
i
δ
i
j
=
n
i
2
s.t. \sum_{j=1}^{n_i}\delta_{ij}=n_{i2}
s.t.j=1∑niδij=ni2
因而文章对网络的剪裁过程可以描述为(当前网络层
C
i
C_i
Ci,包含的卷积参数为
W
C
i
W_{C^i}
WCi,生成的特征图为
O
i
O^i
Oi):
- 1)首先计算生成当前层特征图的每个filter的rank期望 R i = { r 1 i , r 2 i , … , r n i i } ∈ R n i R^i=\{r_1^i,r_2^i,\dots,r_{n_i}^i\}\in R^{n_i} Ri={r1i,r2i,…,rnii}∈Rni;
- 2)对这些rank值进行降序排序得到重排之后的值 R i ^ = { r I 1 i i , r I 2 i i , … , r I n i i i } ∈ R n i \hat{R^i}=\{r_{I_1^i}^i,r_{I_2^i}^i,\dots,r_{I_{n_i}^i}^i\}\in R^{n_i} Ri^={rI1ii,rI2ii,…,rIniii}∈Rni
- 3)按照设定好的剪裁阈值将上面的rank划分为两个部分,也就是重要的部分和非重要的部分;
- 4)移除非重要的部分保留重要的部分之后使用重要部分的参数进行初始化对网络进行finrtune;
2.4 代码实现
文章的思想很简单就是去求取每个filter的rank,之后排序再根据排序删除掉对应的不重要filter。这里对于rank的统计使用的是hook去做的,对应的代码如下(参考:『PyTorch』第十六弹_hook技术):
#get feature map of certain layer via hook
def get_feature_hook(self, input, output):
global feature_result
global entropy
global total
a = output.shape[0]
b = output.shape[1]
c = torch.tensor([torch.matrix_rank(output[i,j,:,:]).item() for i in range(a) for j in range(b)])
c = c.view(a, -1).float()
c = c.sum(0)
feature_result = feature_result * total + c
total = total + a
feature_result = feature_result / total
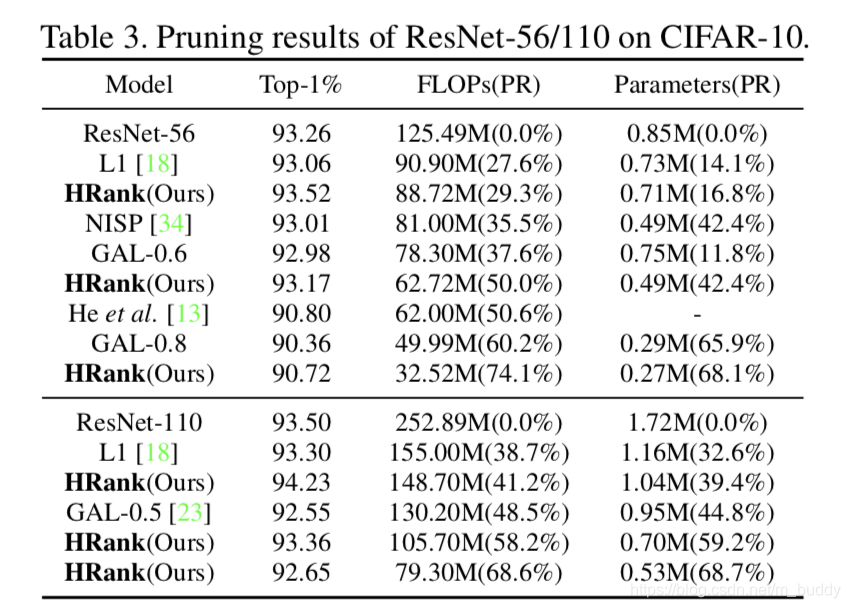
3. 实验结果
CIFAR-10数据集上的结果:
ImageNet数据集上的结果:
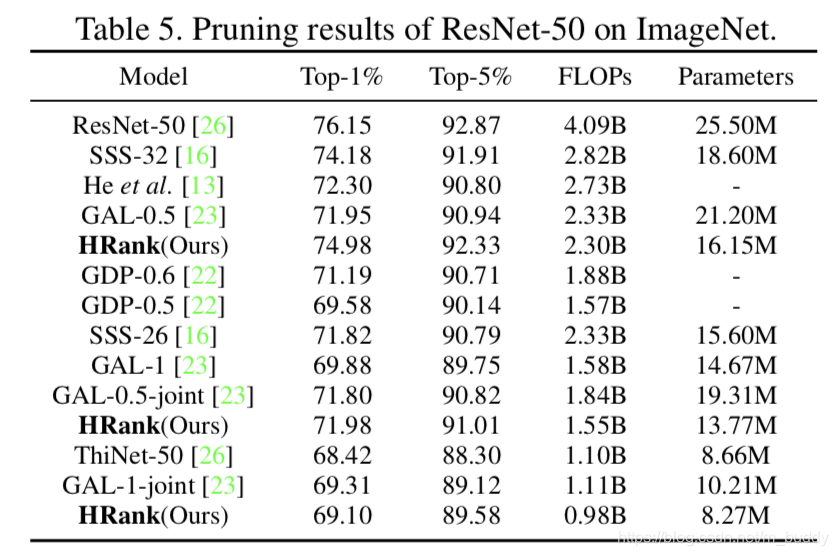





 本文介绍了HRank算法,通过计算特征图的rank来选择并剪裁卷积网络中的filter。实验表明,这种方法在ResNet-110和ResNet-50上实现了较高的FLOPs减少,同时保持了较好的精度。HRank算法避免了输入数据分布的影响,提高了剪裁效率。
本文介绍了HRank算法,通过计算特征图的rank来选择并剪裁卷积网络中的filter。实验表明,这种方法在ResNet-110和ResNet-50上实现了较高的FLOPs减少,同时保持了较好的精度。HRank算法避免了输入数据分布的影响,提高了剪裁效率。
















 3017
3017

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








